兩階段判別嵌入式聚類

支曉斌, 李亞蘭

(1.西安郵電大學 理學院， 陜西 西安 710121； 2.西安郵電大學 通信與信息工程學院， 陜西 西安 710121)

聚類是按照一定的要求和規律對事物進行區分和分類的非監督模式識別過程，被廣泛應用于眾多領域，包括圖像處理、信息檢索、數據挖掘等[1]。其目的是將相似的樣本分配到同一類，不相似的樣本分配到不同類，并揭示數據有意義的結構。在實際應用過程中，通常遇到高維數據集，數據的高維度性不僅增加了算法的計算時間和內存需求，而且由于噪聲效應和空間維度的欠采樣，會對聚類性能產生不利影響，這一現象被稱為“維數詛咒”[2]。因此，高維數據聚類成為聚類分析研究的難點和熱點問題之一，而實際應用過程中普遍存在的高維數據使得對高維數據的聚類分析具有重要意義。

對于高維數據的聚類問題，現存在眾多具有針對性的聚類方法[3-10]。無監督的判別聚類(discriminative clustering, DC)算法[3]將聚類和線性判別分析(linear discriminant analysis, LDA)[4]結合起來，實現了在降維過程中對數據的聚類。由于聚類是在LDA降維后的子空間中完成的，故DC算法常常可以產生比K-均值(K-means, KM)算法[5]更優的聚類效果。從“核”方法的角度考慮，DC算法可等價于判別K-均值聚類(discriminative K-means, DKM)算法[6]，但存在散度矩陣奇異性問題。為避免DC算法中LDA的小樣本問題[7]和克服散度矩陣奇異性問題，判別嵌入式聚類(discriminative embedded clustering, DEC)算法[8]將子空間學習和聚類統一起來，用基于子空間學習的最大間距準則(maximum margin criterion, MMC)[9]降維，以代替DC算法中的LDA降維，來得到最佳的判別向量。但是，這些算法都存在對高維數據計算復雜度高，聚類速度慢的問題。高效判別嵌入式聚類(efficient discriminative embedded clustering, EDEC)算法[10]利用QR[11]分解，并依據MMC對數據進行兩次降維處理，可降低DEC算法的復雜度，但對數據的適應性較差。

為改善DEC算法的運行效率和EDEC算法對數據的適應性問題，本文給出兩階段判別嵌入式聚類(two-stage discriminative embedded clustering, TSDEC)算法。在EDEC算法的基礎上引入正則化因子λ，得到EDEC算法的一種廣義形式。當λ→∞時，TSDEC算法將退化為EDEC算法，而當λ取其它值時，則得到不同于EDEC的新算法，從而提高了EDEC算法對數據的適應性。此外，TSDEC與EDEC算法復雜度相當，主要時間計算復雜度都是O(nmc)(n代表數據樣本的個數，m代表數據維數，c代表類數)，故適合處理比較大的高維數據。

1 DEC算法

為了使得DC 算法能夠有效地對高維數據聚類，并且克服散度矩陣奇異性問題，DEC算法將幾個經典降維方法統一到同一框架下，對數據聚類的同時實現降維，提高了DC算法的聚類效率。平衡參數η取不同值時，DEC算法可將已有的幾個經典降維方法視為特殊情況。例如，當η→0時，DEC算法等價于通過主成分分析(principal component analysis, PCA)[12]先對樣本降維，再對降維后數據用KM算法聚類；當η=1時，DEC算法等價于通過正交質心法(orthogonal centroid method, OCM)[13]先對樣本降維，再對降維后數據用KM算法聚類；當η=2時，DEC算法等價于通過MMC先對樣本降維，再對降維后數據用KM算法聚類；當η→∞時，DEC算法等價于通過正交最小二乘判別分析(orthogonal least squares discriminant analysis, OLSDA)[14]先對樣本降維，再對降維后數據用KM算法聚類。

X=(x1,x2, …,xn)。

聚類的目標是將所有數據樣本分成c類，設第j類為Xj，其中含有nj個數據樣本(j=1,2,…,c)，以這些數據樣本為列向量可構成m×nj的數據矩陣Xj。

DEC算法可以描述為優化問題

maxJDEC(W,H)=
tr {WT[Sb+(1-η)Sw]W},
s.t.WTW=I。

其中，η為平衡參數，W為樣本由高維空間映射到低維空間的待求變換矩陣，矩陣H=(hij)n×c為待求隸屬度矩陣，若數據樣本xi屬于第j類，則hij=1；否則，hij=0。類內散度矩陣Sw和類間散度矩陣Sb分別定義為

矩陣Hw和Hb分別定義為

Hw=[X1-v1e1,…,Xc-vcec],

(1)

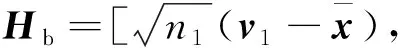
(2)

其中，ej=(1,2,…,1)∈nj為行向量。

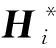
以m′代表嵌入子空間中數據的維數，T代表算法運行的迭代次數，那么，DEC算法的時間計算復雜度為O[(nm2+ncm′)T]。

2 TSDEC算法

TSDEC算法首先用奇異值分解方法代替EDEC算法中的QR分解對正則化的類間散度矩陣做預處理，對數據矩陣進行初次降維；然后，在低維空間利用DEC算法中的經典降維方法對數據進行二次降維；最后，對降維兩次的數據進行聚類。初次降維后數據的維數可以達到c維，故可使第二次降維過程變得更加高效，提升算法對高維數據的聚類效率。另外，引入正則化過程，得到EDEC算法的一種廣義形式，以提高EDEC算法對數據的適應性。

TSDEC算法詳細步驟如下。

步驟1對原始數據集執行規范化和中心化過程，并初始化類標簽矩陣H。

步驟2根據(2)式構造矩陣Hb。

步驟3對矩陣Hb進行奇異值分解,得

Hb=UΣVT,

其中，U∈m×m和V∈c×c為正交矩陣，Σ∈m×c為對角陣。

步驟4Σ的前c行c列構成方陣Σ1，以Ic代表c階單位矩陣，將奇異值矩陣正則化為

再令

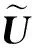
步驟5令

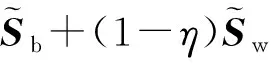
W=(w1,w2,…,wc)。

步驟7利用求得的特征子空間，計算最優變換矩陣G=QW。

步驟8利用y=GTx對數據進行投影變換，在降維后的投影空間中對數據執行KM聚類算法，更新隸屬度矩陣H。如果滿足‖H-H0‖<ε，則停止計算；否則，令H0=H，轉回步驟3。ε為停止閾值。

TSDEC算法將DEC算法的主要計算復雜度由O(nm2)降低為O(nmc)，通常對于高維數據集有m?c，因此，TSDEC算法在運行速率上與EDEC算法相當，而比DEC算法更高效。

TSDEC算法在EDEC算法的基礎上增加了步驟4中的奇異值矩陣正則化過程，即令

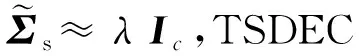
3 實驗結果及分析

將TSDEC算法與KM算法、DEC算法和EDEC算法在不同正則化參數下對6個數據集進行對比性實驗。

3.1 實驗設置

實驗選取6個數據集，包括3個UCI數據集[15]Wine、Letter(abc)、Satimage，一個文本數據集[16]Doc，一個手寫體數據集[17]MNIST和一個基因表達數據集[18]Global Cancer Map(GCM)。數據特性如表1所示。

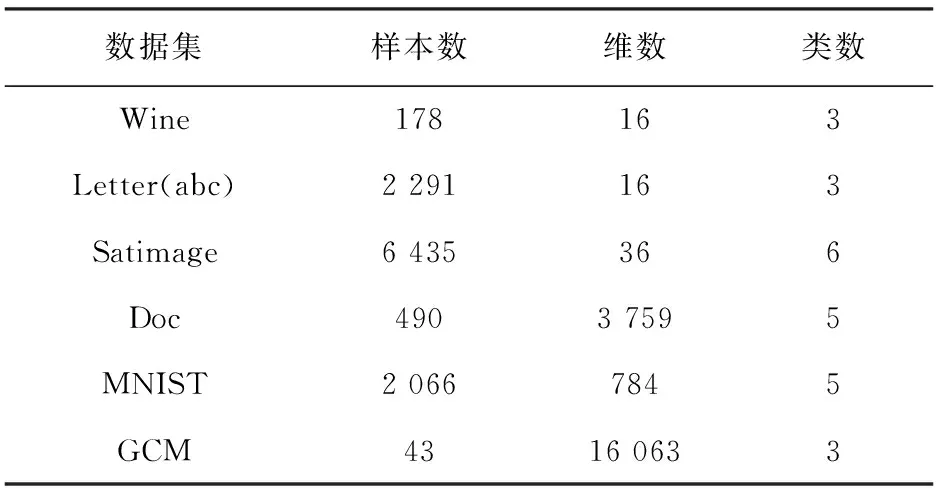
表1 6個數據集的相關特性

實驗在Intel Core i5 2.8 GHz CPU，4 GB內存Window 10環境下的電腦上進行運算。為了防止算法陷入局部最優，算法運行10次后取平均值。最大運行迭代次數設置為100，停止閾值ε設為10-5。

3.2 準確度測試

針對6個數據集，平衡參數η依次取值為2、1、1、∞、2、2，正則化參數λ的取值集合為{10-6，10-5，10-4，10-3，10-2，10-1，100，101，102，103，104，105，106}。4種算法在各數據集上的聚類性能隨正則化參數的變化趨勢如圖1所示。其中，DEC算法在GCM數據集上運行內存溢出，無法獲得聚類準確度，而KM算法、DEC算法和EDEC算法的聚類準確度各是一條不隨正則化參數λ變化的直線。

由圖1所示聚類結果可知，對于大多數正則化參數λ，TSDEC算法的聚類準確度優于其它3種算法。當正則化參數λ越大時，TSDEC算法的聚類準確度越接近于EDEC算法，這驗證了TSDEC算法是EDEC算法的廣義形式，且當正則化參數λ趨于無窮大時，EDEC算法成為TSDEC算法的特例。

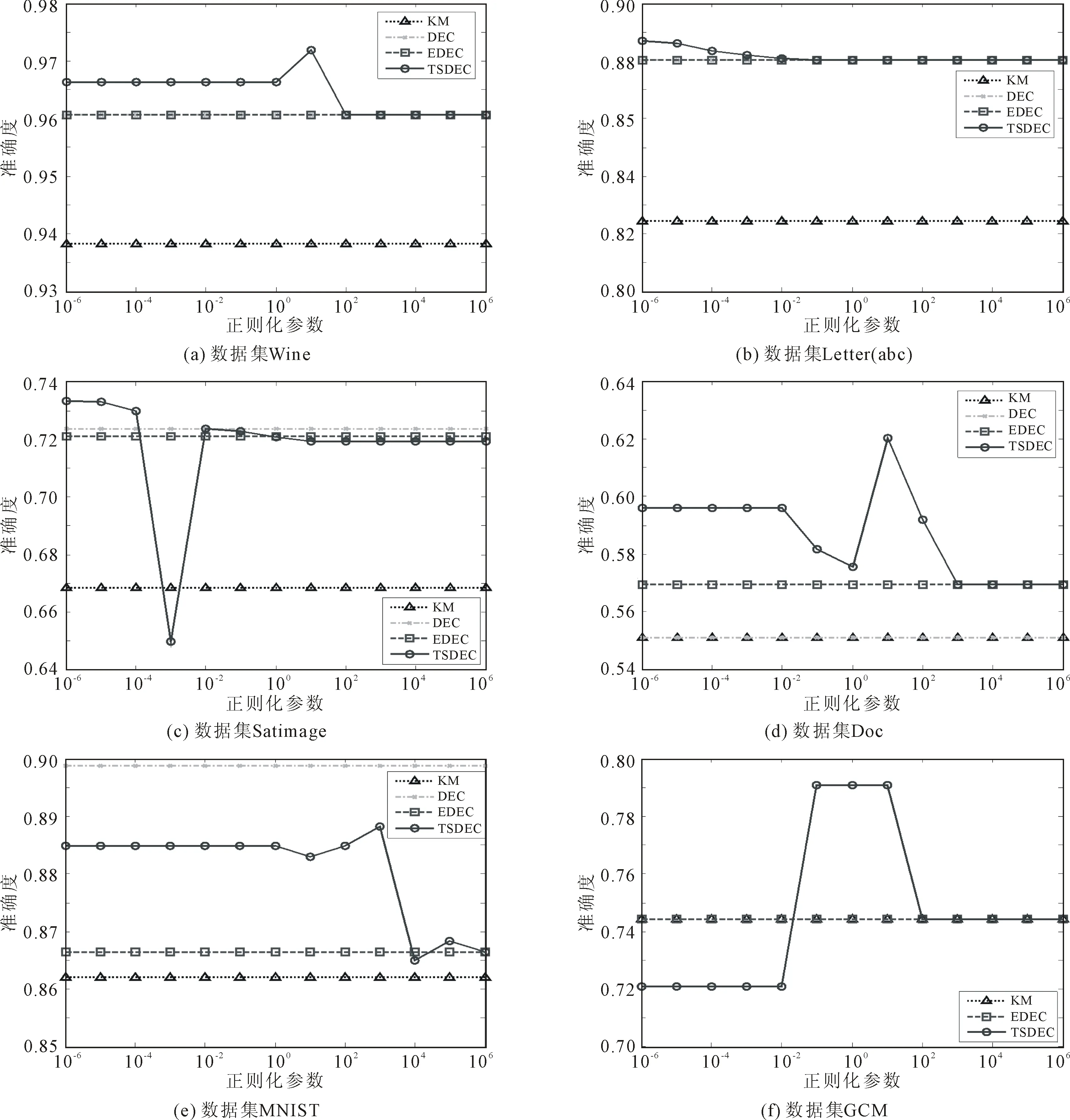
圖1各數據集聚類結果

不同正則化參數下的最優聚類準確度及平均聚類準確度結果如表2所示。其中，“—”表示DEC算法在相應參數下內存溢出。

由表2可知，在大多數數據集上，TSDEC算法的最優聚類準確度及平均聚類準確度優于KM算法、DEC算法EDEC算法。

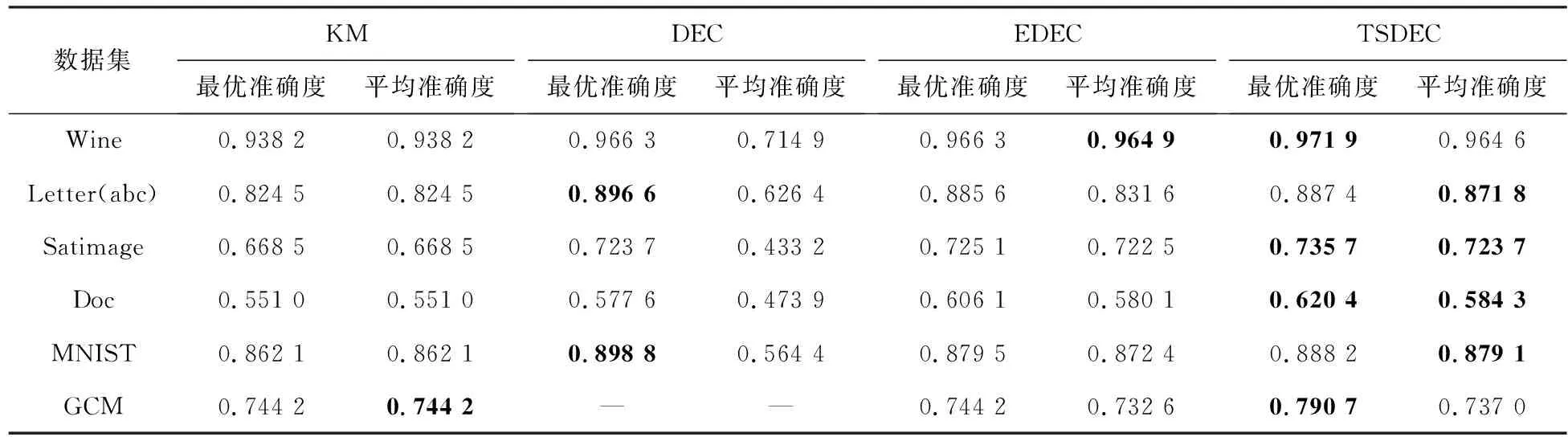
表2 4種算法在6組數據集上的聚類準確度

3.3 運行時間測試

4種算法對6個數據集在不同正則化參數取值下的運行時間如圖2所示。其中，DEC算法在GCM數據集上運行內存溢出，無法獲得運行時間，而KM算法、DEC算法和EDEC算法的運行時間各是一條不隨正則化參數λ變化的直線。

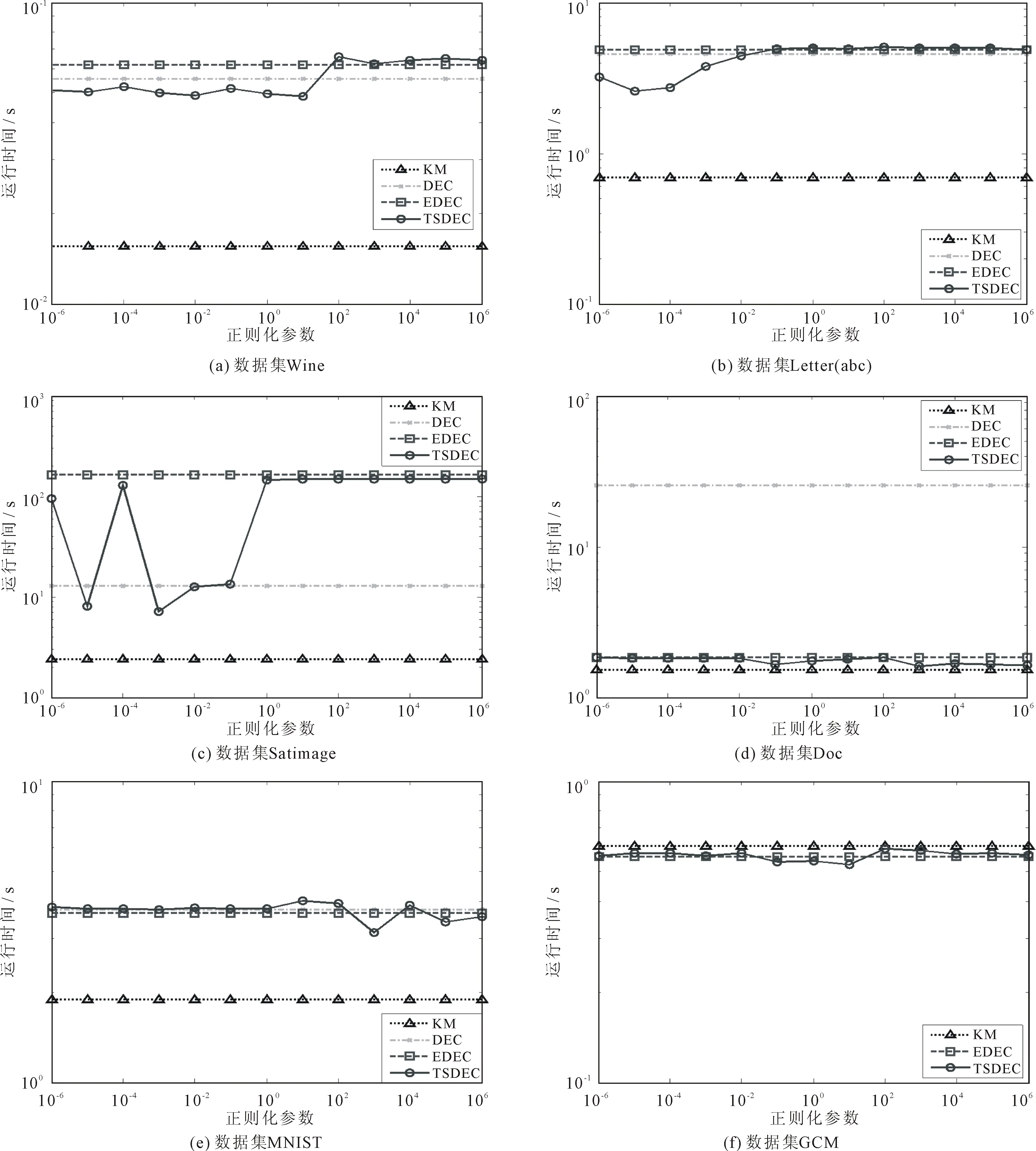
圖2 各數據集上4種算法的運行時間

由圖2可知，除了GCM數據集，KM算法在其它數據集上的平均運行效率最高，運行時間是4種算法中最少的，但聚類準確度相較于其它算法有所偏低。TSDEC算法與EDEC算法的運行效率基本持平，且當正則化參數λ越大時，TSDEC算法的運行時間越接近于EDEC算法。對于兩個高維數據集DOC和GCM而言，TSDEC算法和EDEC算法的運行效率明顯優于DEC算法。

各數據集在不同正則化參數下的最優聚類準確度和平均聚類準確度相對應的運行時間如表3所示。其中，To和Tm分別表示各算法的最快運行時間和平均運行時間， “—”表示DEC算法在相應參數下內存溢出。由表3可知，除KM算法外，在大多數數據集上，EDEC算法的平均運行效率較高，而TSDEC算法的最優運行效率相較于DEC算法和EDEC算法有所提高。

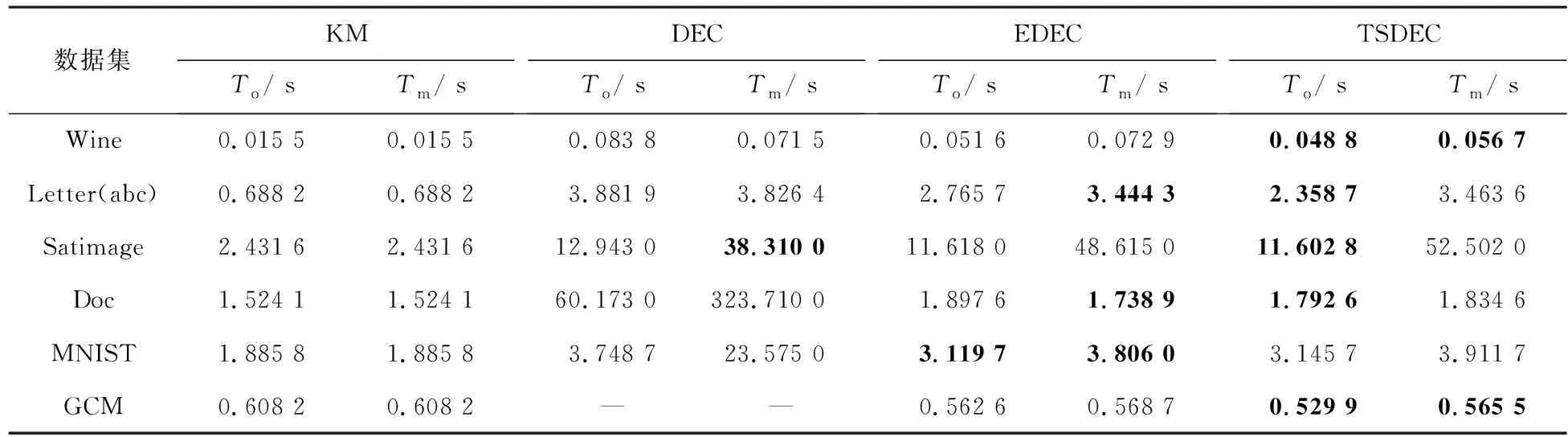
表3 4種算法在6組數據集上的運行時間

4 結語

TSDEC算法通過對正則化的類間散度矩陣做奇異值分解，得到數據的降維預處理，再對降維后數據進行判別嵌入式聚類，可以看作是在EDEC算法中引入類間散度矩陣正則化過程所得到的一般性算法。TSDEC算法將DEC算法的主要時間復雜度由O(nm2)降低為O(nmc)。實驗結果表明，正則化過程的引入提高了原EDEC算法對數據的適應能力。對大多數的數據集而言，TSDEC算法的聚類準確度(包括平均準確度和不同參數下的最優準確度)優于DEC與EDEC算法。TSDEC算法的運行效率與EDEC算法相當，對于高維數據集，二者的運行效率均優于DEC算法。TSDEC為線性聚類算法，為了提高算法對非線性可分數據的聚類性能，下一步的工作是利用核技巧[19]給出TSDEC算法的核版本。