變風量末端裝置的基于IPSA-DE算法室溫PIλDμ-送風量PI串級控制器的數值仿真

李鵬波 李紹勇 吳宗禮 李海林 魏先宏

?

變風量末端裝置的基于IPSA-DE算法室溫PIλDμ-送風量PI串級控制器的數值仿真

李鵬波 李紹勇 吳宗禮 李海林 魏先宏

（蘭州理工大學土木工程學院 蘭州 730050）

目前，空調房間配用的變風量末端裝置（Variable Air Volume Terminal，VAV-TMN）往往采用整數階PID-P串級調節方式，這帶來了室溫控制誤差和超調量較大以及調節時間較長等問題。鑒于此，提出了空調VAV-TMN的室溫分數階PID-送風量PI的串級調節器設計方法。首先，綜合分析空調工藝和自動控制的相關要求，對室內溫度對象、溫度和風量測量變送單元、送風量執行單元分別進行建模，確定主控制器為室溫分數階PID控制器（Indoor Temperature Fractional Order Proportional Integral Derivative Controller，IT-FOPIDC）和副控制器為送風量PI控制器（Sending Air Volume Proportional Integral Controller，SAV-PIC）的控制策略。其次，基于改進的自適應差分進化（Improved Parameter Self-adaptive Differential Evolution，IPSA-DE）算法來分別整定出IT-FOPIDC和SAV-PIC的控制參數最佳值。最后，借助MATLAB/Simulink工具，對該空調VAV-TMN的室溫PIλDμ-送風量PI串級調節系統進行組態和數值模擬相應的控制效果。結果表明，該串級控制系統在理論上是可行的，且室溫的控制效果明顯優于基于Ziegler-Nichols整定法和DE算法的整數階室溫PID-送風量PI串級調節系統。

空調變風量末端裝置；室溫分數階PID控制器；串級控制；改進的參數自適應差分進化算法；數值仿真

0 引言

空調系統（Air-conditioning System，ACS）在建筑空間的廣泛應用，滿足了人們對房間溫度、濕度和潔凈度等的舒適性需求，提升了工作與學習效率和生活品質。同時，ACS運行也帶來了建筑能耗增大的問題[1]。隨著空調工藝新技術和理念的不斷出現，如變制冷劑流量方式、冷凍、冷卻水泵與送、回風機的變頻技術和室外新風溫度補償控制方式等在實際ACS或工程中得到了應用，起到了節能降耗的效果。其中，變風量空調技術由于其優越的節能性受到了國內外的重視[2]。相應的變風量空調系統是由組合式空調機組（Air Handling Unit，AHU），送、回風子系統，變風量末端裝置（VAV-TMN）等組成，其運行與管理屬于一個設備多、多工況切換和多參數控制的復雜與綜合過程，主要包括室內溫度、送風量及送風溫度、新風溫度和風量、回風溫度和風量和AHU的啟停等主要控制內容。由于空調VAV-TMN安裝在空調房間內，在送風溫度保持不變的前提下，其送風量的多少對于人們舒適性的關鍵參數—室內溫度的影響顯著。但是，空調房間對象具有非線性、時滯、結構參數不確定等特性，使得目前的常用控制方式，如VAV-TMN室溫PID單回路控制系統會出現室溫的余差、超調量和調節時間等控制指標達不到預期的空調工藝需求的狀況[2]。

針對上述存在的問題，本文提出了空調VAV-TMN的室溫PIλDμ-送風量PI串級調節器設計方法。其中，IT-FOPIDC作用在主回路（Main Loop，ML），定值調節。SAV-PIC作用于副回路（Auxiliary Loop，AL），接受IT-FOPIDC輸出的信號作為其設定值，隨動調節。此外，本文還提出了IPSA-DE算法，分別施用于IT-FOPIDC的5個參數（P,M、I,M、D,M、和）和SAV-PIC的2個參數（P,A和P,A）整定，獲取更為合理的控制器參數值。這樣，既發揮了IT-FOPIDC對于空調房間對象所具備的非線性和大時滯等特性的強適應性作用，SAV-PIC又輸出了更為精準的控制指令給VAV-TMN的送風閥，確保送入空調房間的冷、熱風量動態地適應空調負荷變化，滿足室溫達標和克服室內壓力n波動以及Ziegler-Nichols整定法無法應用于分數階PID控制器參數整定的缺陷。

1 空調VAV-TMN的室溫PIλDμ-送風量PI串級控制系統的構建

空調系統中實際的控制對象大多可用高階微分方程來描述。但為了分析簡便，并且使控制精度能夠滿足要求，通常用低階模型來近似描述控制對象的動態特性。本文提出的室溫PIλDμ-送風量PI串級控制系統屬于基于模型的控制范圍，所以需要對該系統的各個組成環節進行數學建模，獲得相應的輸入與輸出關系式。

1.1 空調房間溫度對象的輸入/輸出特性

室溫n是衡量室內舒適性的重要參數，也是該串級調節系統的被控參數。由文獻《變風量空調系統的建模與控制仿真》中，空調房間溫度對象屬于具有較大時滯、大慣性等特性的熱工過程對象，其輸入/輸出特性可用一階慣性環節加純滯后的傳遞函數來表述，即：

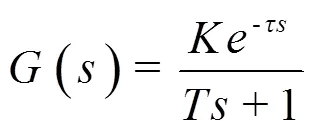
式中，為時間常數；為空調房間純滯后時間；為調節通道放大系數。根據文獻[2]給出的建模原則該空調房間的數學模型可表示為：

1.2 室溫和送風量測量變送器的輸入/輸出特性

室溫測量變送器和送風量變送器起著實時地測量室溫大小與送風量多少的作用，分別作用在ML和AL的反饋通道上。對應的傳遞函數分別如式（3）和（4）所示[2,3]：

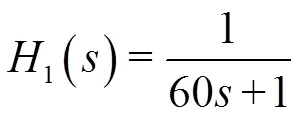
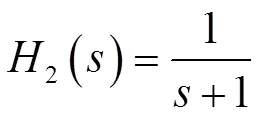
1.3 送風量執行器的輸入/輸出特性

送風量執行器（Sending Air Volume Actuator，SAVA），簡稱送風閥。它接受副控制器的控制指令，改變其開度，確保送入空調房間的冷、熱風量與空調負荷變化相適應。SAVA的傳遞函數如下[3]：

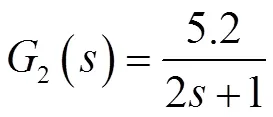
1.4 室溫PIλDμ和送風量PI控制器的輸入/輸出特性

如上所述，室溫PIλDμ控制器作用在ML，發揮其適應被控對象的非線性、大時滯等特性和克服主要干擾的作用。其輸入信號為空調工藝要求的室溫設定值n,set，對應的傳遞函數如下：

送風量PI控制器作用在AL，發揮它克服次要干擾和隨動調節送風量適應空調負荷變化的作用。其輸入信號為室溫PIλDμ控制器的輸出，輸出信號為VAV-TMN送風量的大小，對應的傳遞函數如下：

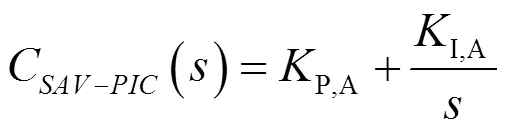
式中，P,M、I,M、D,M分別為IT-FOPIDC比例增益、積分增益、微分增益；、分別為IT-FOPIDC積分階數、微分階數；P,A、I,A分別為SAV-PIC比例增益、積分增益。

因此，本文構建的空調VAV-TMN的室溫PIλDμ-送風量PI的串級調節系統方框圖，如圖1所示。

圖1 室溫分數階PIλDμ-送風量PI的串級調節系統方框圖

該串級調節系統的調節過程簡述如下：室溫測量變送器將反映室溫n大小的信號1上傳給IT-FOPIDC，與n,set相比較，產生1=n,set-n。1被輸送到IPSA-DE算法上，實時整定出IT-FOPIDC和SAV-PIC所需的控制參數值。這樣，基于不斷更新的P,M、I,M、D,M、、、P,A和I,A，IT-FOPIDC和SAV-PIC串級作用，連續輸出適應空調負荷變化的控制指令給VAV-TMN送風閥，改變其開度，給空調房間送入恰當的冷、熱風量，滿足空調工藝要求n≈n,set及其他控制指標，如合理的衰減比、較小的超調量和較短的調節時間等。

2 基于IPSA-DE算法的PIλDμ和PI控制器參數的整定

2.1 標準DE算法

差分進化（Differential Evolution, DE）算法是由Rainner Stom和Kenneth Price[4]提出的一種模擬自然界生物種群進化的啟發式搜索算法，它是以“優勝劣汰，適者生存”為原則的一種新興的進化計算技術。通過群體內個體之間的合作與競爭指導優化搜索，DE算法保留了基于種群的全局搜索策略，采用編碼、差分的簡單變異操作和一對一的競爭生存策略，降低遺傳選擇的復雜性。同時，差分進化特有的記憶能力可以動態跟蹤當前搜索，以隨時改變其搜索策略。具有較好的全局收斂能力和魯棒性。

（1）生成初始群體

在空間里隨機產生滿足約束的NP個個體，該種群中NP個個體進行如下隨機初始化：

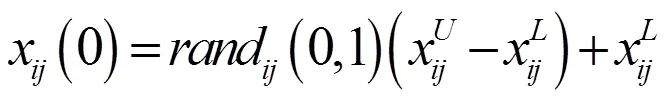
（2）差分變異

差分變異是差分進化的關鍵步驟，從群體中隨機選擇3個個體x、x和x，且≠，則基本變異為：

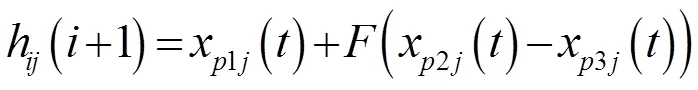
如果無局部優化的問題，變異操作為：

其中，x（）-x（）為差異化向量；為縮放因子；p、p、p為在個體種群中的序號。

（3）交叉操作

交叉是為了增加種群的多樣性，具體操作如下：

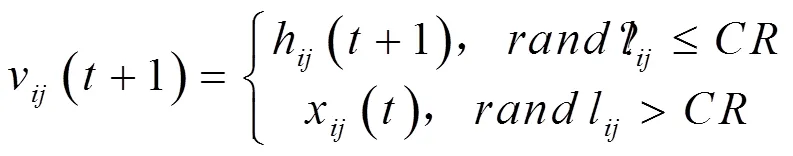
（4）選擇操作

在選擇階段使用一種貪婪準則，為了確定x（）是否成為下一代成員，試驗向量v（）和目標向量x（）對評價函數進行比較：

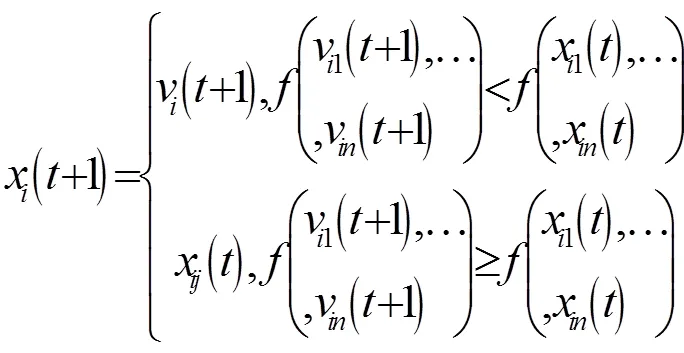
經過變異交叉選擇后，產生新一代，但并不意味著DE算法的結束，而是經過重復以上步驟直到滿足設定的約束條件為止。

2.2 改進的PSA-DE算法

標準差分進化具有收斂速度快，較好的全局收斂能力和魯棒性等特點。考慮到標準DE算法在執行時，其縮放因子、交叉因子以及群體規模NP對于搜索結果影響顯著，和固定不變，容易早熟陷入局部最優。

因此，本文提出IPSA-DE算法。通過適當地改變和，來獲取全局最優和克服收斂早熟等問題。調整和的數學關系式，分別如式（12）和（13）所示。

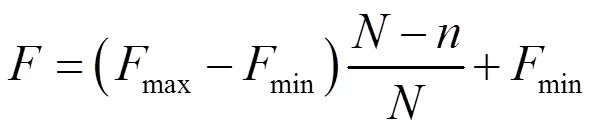
式中，max和min為選定變異因子的最大值和最小值；為最大進化代數；為當前進化代數。

在搜索初期，較大時有利于擴大搜索空間，保持種群的多樣性；在搜索的后期，較小有利于縮小搜索范圍，提高其搜索的精度和收斂速度，一般取在[0.3,0.6]之間。

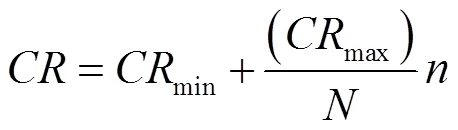
式中，max為交叉因子的最大值；min為交叉因子的最小值。

這樣，越小種群的多樣性越小，容易早熟，越大收斂速度越大，但是由于擾動大于群體差異度可能導致收斂速度過慢。一般選在[0.6,0.9]之間。

因此，相比較標準DE[5]，本文提出IPSA-DE算法能夠隨著種群代數NP的增加，線性遞減，線性遞增，不僅能在初期保持種群的多樣性，而且保證后期的收斂速度快，全局收斂和魯棒性。

2.3 基于ISPA-DE的PIλDμ和PI控制器參數整定算法

控制器參數整定的目標是在期望的目標參數達到最優時，獲取對應的控制器參數值，進而輸出控制指令到執行單元，產生調節作用，克服干擾，使得被控參數等于或接近設定值。由于IT-FOPIDC和SAV-PIC分別有5個參數[P,M，I,M，D,M，，]和2個參數[P,A，I,A]需要整定，且考慮到避免室溫超調量過大。所以，基于文獻[5]，為了避免室溫超調，采用懲罰功能，將室溫超調量作為尋優指標的一項，本文提出的目標函數如下式所示。

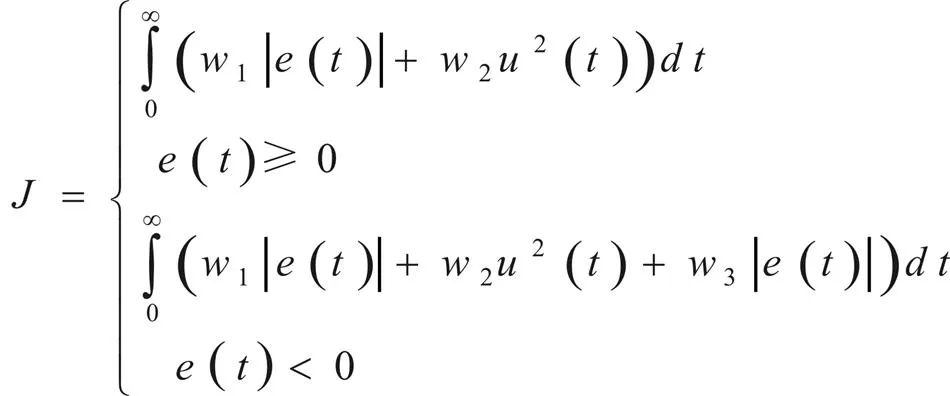
式中，（）為室溫設定值與室溫測量值的差值1，℃，（）為SAV-PIC的輸出指令2，mA·DC，1、2、3為權值，這里取值1=0.999，2=0.001，3=10。

因此，將7個控制器參數構成向量形式[P,M，I,M，D,M，，P,A，I,A]T。基于IPSA-DE，進行以式（14）中的作為最小化的目標函數尋優，獲取相應的控制器參數最佳值P,M*，I,M*，D,M*，*，*P,A*和I,A*。具體的PIλDμ和PI控制器參數整定算法流程如下：

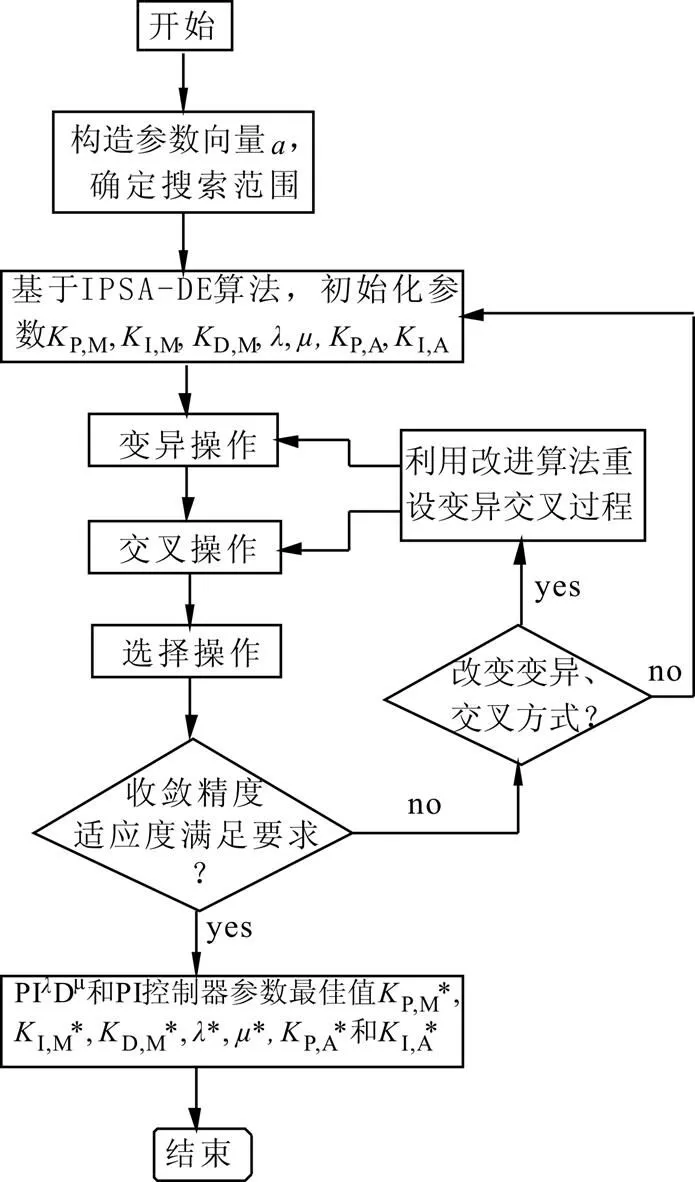
圖2 基于ISPA-DE的PIλDμ和PI控制器參數整定程序流程圖

3 KP,M*，KI,M*，KD,M*，λ*，μ*，KP,A*和KI,A*的尋優求解

本文通過Simulink來搭建本文所提出的串級系統模型，如圖3所示。通過控制單一變量的變化，來整定相應P,M，I,M，D,M，，P,A，I,A的取值范圍。

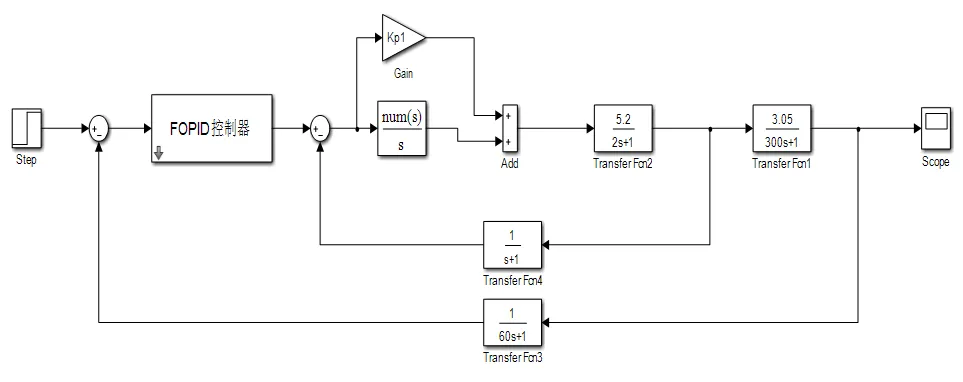
圖3 確定7個控制器參數取值范圍的Simulink模型

首先，預置I,M=D,M=I,A=0，P,A==1，進行仿真實驗，來整定P,M的取值范圍，P,M變化如圖4所示。

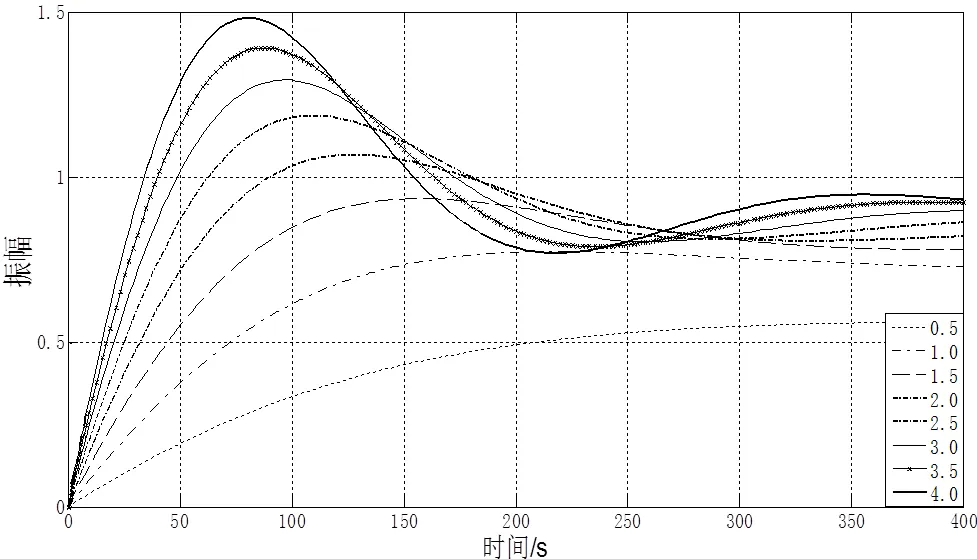
（a）P,M取0.3-2.3

（b）P,M取4.5-12.5

圖4 隨著P,M的變化，控制的系統階躍響應響應圖

Fig.4control System step response with the change of withP, M

綜上分析得P,M可取值為{0.5,6.0}，其余參數取值與P,M類似，例如要整定I,M的取值范圍，可預置P,M為{0.5,6.0}的任意值，這里取P,M=1.5，D,M=I,A=0，P,A==1，來整定I,M的取值為{0.001,0.02}，其余參數的整定在這里不再贅述，其中，D,M的取值為{20,50}，的取值為{1.0,1.3}，的取值為{0.59,0.99}，P,A的取值為{0.3,0.9}，I,A的取值為{0.001,0.02}。所以，辨識向量的辨識參數限定范圍為：

Min=[0.5，0.001，20，0.97，0.59，0.3，0.001]

Max=[6.0，0.020，50，1.3，0.99，0.9，0.020]

基于圖2所示的ISPA-DE的PIλDμ和PI控制器參數程序流程圖，將該ISPA-DE算法的相關參數值設定為：=30；max=0.6；min=0.3；max=0.9；min=0.6；=30。經過30代的進化，經整定得該串級控制系統控制器的7個參數最優辨識結果為：

=[1.0000，0.0070，50.0000，0.9789，0.7437，0.8247，0.0035]

即該系統的IT-FOPIDC的傳遞函數為：

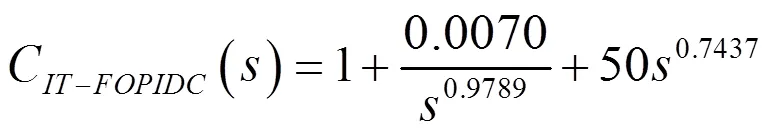
SAV-PIC的傳遞函數為：

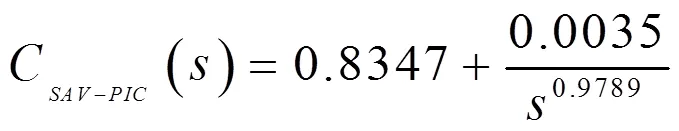
基于文獻[8]中的Ziegler-Nichols整定法，可得到單回路室溫PID控制器的控制參數：

1=[1.0194，0.0018，50.0000，0.3000，0.0010]

對于標準DE算法參數選取：=0.8；=0.6。經目標尋優到的相應IT-FOPIDC和SAV-PIC控制器參數最優辨識結果為：

2=[1.0194，0.0018，50.0000，1.1888，0.8588，0.3000，0.0010]

同樣的，基于IPSA-DE算法整定的IT-PIDC和SAV-PIC控制器參數辨識結果為：

3=[1.4176，0.0033，49.1641，0.8856，0.0010]

最后，運用標準DE算法整定的IT-PIDC和SAV-PIC控制器參數辨識結果為：。

4=[1.0581，0.0033，50.0000，0.6135，0.0200]

將上述的整定的參數、1、2、3、4，在MATLAB/Simulink軟件中模擬仿真，得到相應的控制系統的階躍響應輸出如圖5所示。

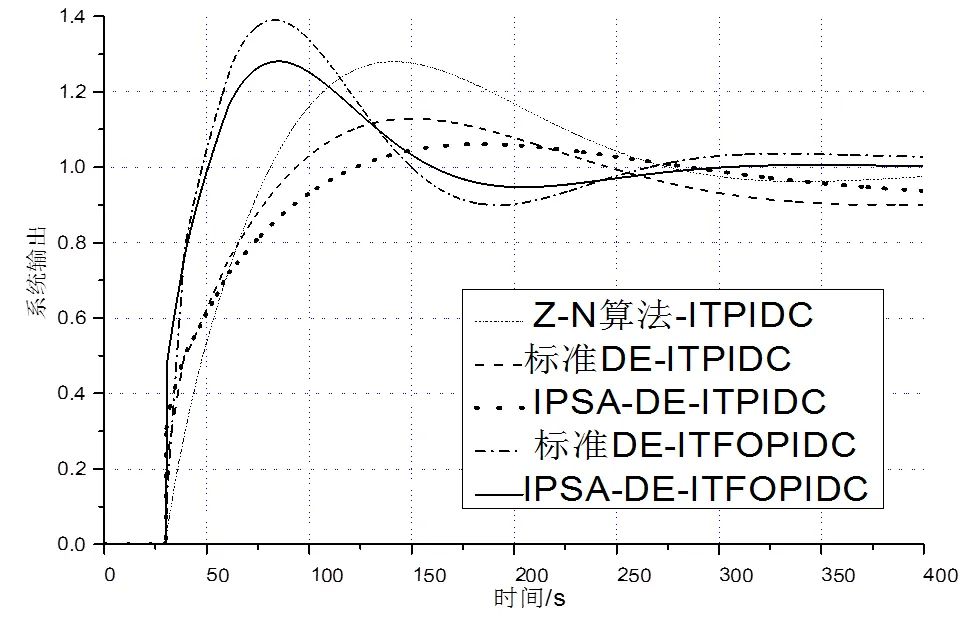
圖5 基于不同控制器參數整定算法的相應控制系統的階躍響應曲線

基于圖5的分析，匯總不同控制器參數整定算法對相應的控制系統的階躍響應輸出的影響，如表1所示。表中，n,set為室內溫度設定值，℃；n,max為室內溫度變化的最大值，℃；為室內溫度的穩態誤差，%；為控制系統的調節時間，s。

表1 不同控制器參數整定算法的性能分析

分析表1可知，IPSA-DE算法的整定效果優于標準的DE算法和Z-N整定算法。IPSA-DE算法整定結果具有較小的超調量、較小的靜態誤差和較快的調節時間。

4 數值仿真

根據第1節所述的空調房間溫度對象、室溫和送風量測量變送器、送風閥、室溫PIλDμ和送風量PI控制器的傳遞函數和圖1所示的室溫PIλDμ-送風量PI串級控制系統的方框圖，通過Matlab/Simulink tool進行組態，該串級控制系統的Simulink仿真模型，如圖6所示。

首先，在空調冬季的工況下：室內初始溫度為10 ℃，n,set=25±1 ℃。仿真運行圖6所示的室溫PIλDμ-送風量PI串級控制系統，相應的室溫變化曲線如圖7所示。

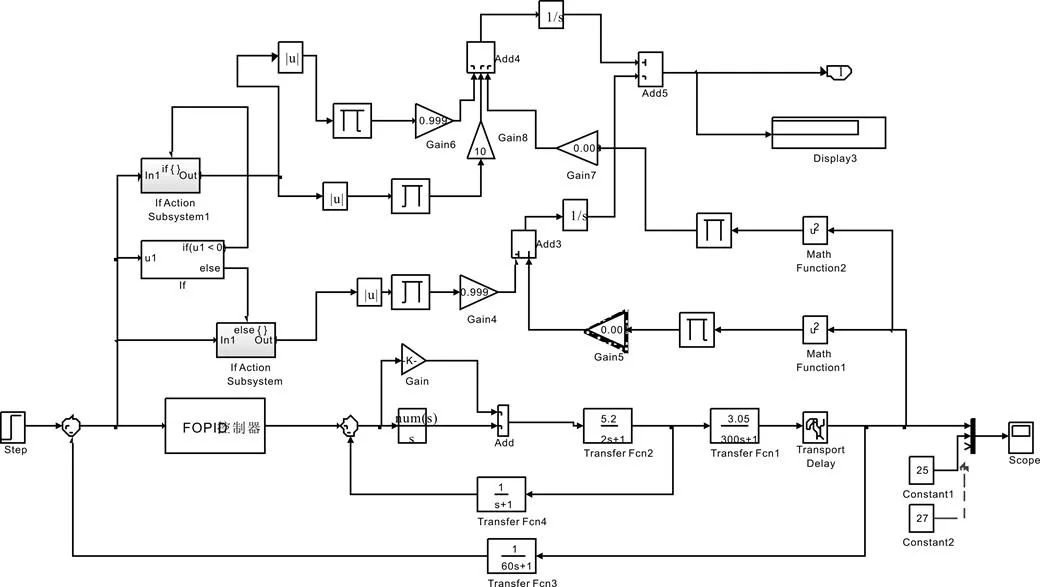
圖6 PIλDμ-PI串級控制系統Simulink仿真模型組態圖

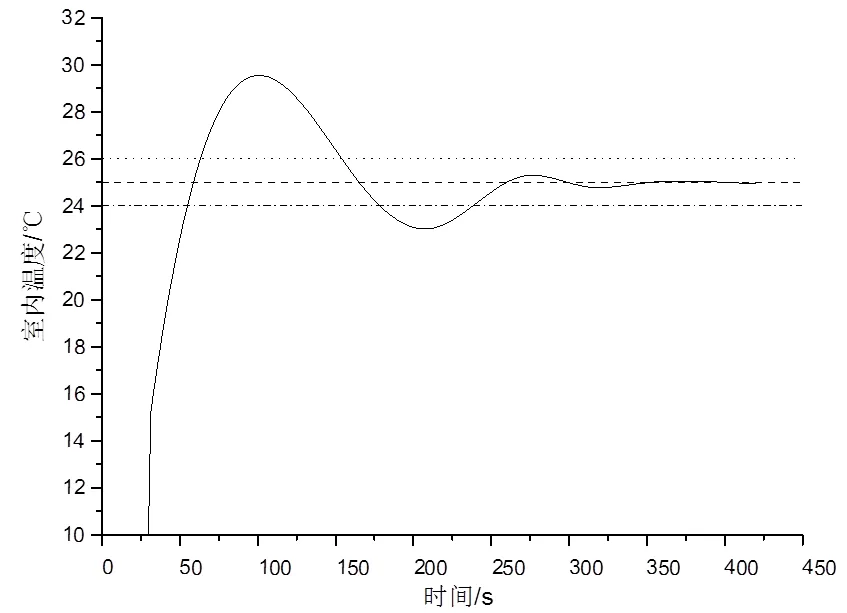
圖7 空調冬季工況下，室內溫度變化曲線圖

然后，在空調夏季的工況下：室內初始溫度為35 ℃，n,set=27±1 ℃。同樣地，仿真運行圖6的室溫PIλDμ-送風量PI串級控制系統，相應的室溫變化曲線如圖8所示。

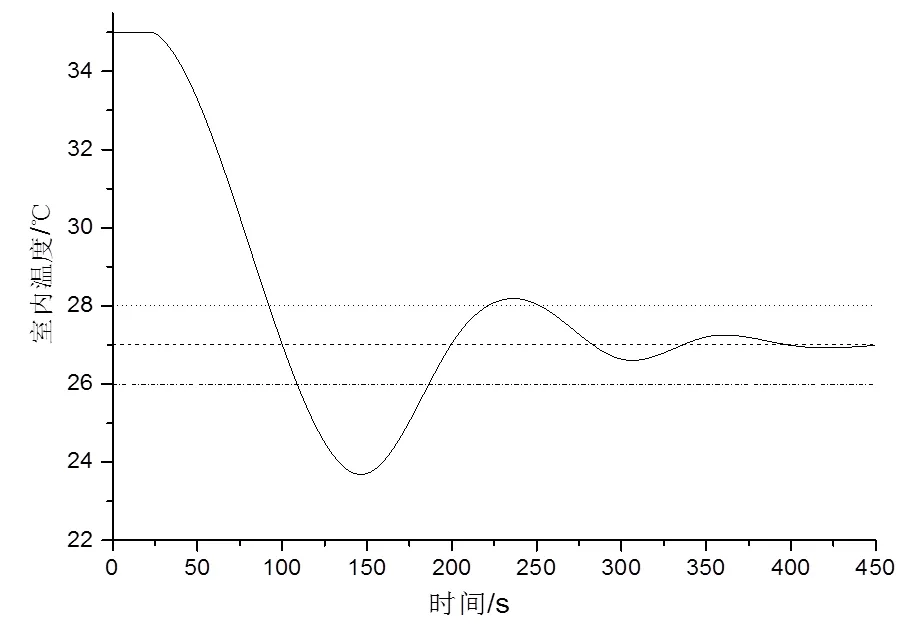
圖8 空調夏季工況下，室內溫度變化曲線圖

由冬、夏季的室內溫度變化曲線圖可以看出，在基于IPSA-DE算法下整定的T-FOPIDC和SAV-PIC控制器參數，具有較好的控制效果。在冬季室內溫度的變化曲線可以看出在250 s時可以滿足室內設計溫度的需求，在夏季室內溫度的變化曲線可以看出在270 s時能滿足室內的設計溫度需求。且具有較好的穩態誤差和動靜態性能。滿足空調工藝室內溫度的調節需求。

5 結論

本文基于IPSA-DE算法即對標準DE算法的放縮因子和交叉因子，引入不同的函數進行自適應調整，將優化后的最適應的一組參數作為控制系統的最優值。經過實驗仿真，仿真結果表明：通過設計IPSA-DE算法整定IT-FOPIDC和SAV-PIC控制器參數具有更快的搜索速度，更高的整定效率。而FOPIDC與PIDC相比，又具有較高的精度。經仿真分析，系統超調量及穩態誤差得到了很好的控制，系統具有調節迅速、更好動靜態性能。

[1] 王軍.模糊解耦控制技術在VAV中的應用[J].陜西師范大學學報,2002,30(2): 28-35.

[2] 郭金錢.變風量空調系統的建模與控制仿真[D]青島:青島理工大學,2014:54-60.

[3] 黃麗蓮,周曉亮,項建弘.分數階PID控制器參數的自適應設計[J].系統工程與電子技術,2013,35(5):1064- 1069.

[4] 周曉亮.改進差分進化算法在分數階控制系統中的應用[D].哈爾濱:哈爾濱工程大學,2013:24-32.

[5] 劉金琨.先進PID控制MATLAB仿真(第4版)[M].北京:電子工業出版社,2016:329-339.

[6] 齊乃明,秦昌茂,王威.分數階系統的最優Oustaloup數字實現算法[J].控制與決策,2010,2(10):1598-1600.

[7] Krishna B T.Studies on fractional order differentiators and integrators: A survey[J]. Signal Processing, 2011, 91(2):386-426.

[8] 王亞剛,許曉鳴,邵惠鶴.基于Ziegler-Nichols頻率響應方法的自適應PID控制[J].控制工程,2012,19(4): 607-618.

[9] 王文修,謝軍龍,劉鑫,等.船用VAV末端裝置風量傳感器布置對風量傳感特性的影響研究[J].制冷與空調,2017,31(4):396-400.

[10] Vinopraba T, Sivakumaran N, Narayanan S. Design of internal model control based fractional order PID controller[J]. Control Theory Application, 2012,10(3): 297-302.

[11] 于蓮芝,成羚羚.分數階PID控制運用于勵磁控制系統[J].上海理工大學學報,2013,35(4):404-408.

[12] 王亞峰,李紹勇.空調房間溫度模糊分數階PID控制器的設計[J].制冷與空調,2014,28(4):451-456.

Numerical Simulation of a Indoor Temperature PIλDμ- Sending Air Volume PI Cascade Controller Based on IPSA - DE algorithm for Variable Air Volume Terminal

Li Pengbo Li Shaoyong Wu Zongli Li Hailin Wei Xianhong

( School of civil engineering, Lanzhou university of technology, Lanzhou, 730050 )

At present, integer order PID-P cascade control method is usually adopted for the variable air volume terminal (VAV-TMN) in an air-conditioned room, which brings about the problems of larger control error and overshoot of indoor temperature and the longer adjustment time, etc. In view of this, this paper presents a design method of a cascade fractional order regulator on indoor temperature PID plus sending air volume PI for the VAV-TMN in an air-conditioning room. First, based on the analysis of the relevant requirements of air conditioning process and automatic control, the indoor temperature plant, measurement transmission units of temperature and air volume, and actuator of sending air volume are modeled, respectively, and then the main controller is indoor temperature fractional order PID controller (IT-FOPIDC) and the secondary one is sending air volume PI controller (SAV-PIC) in our control strategy. Secondly, the optimal values of controller parameters of IT-FOPIDC and SAV-PIC are adjusted respectively by an improved parameter self-adaptive differential evolution (IPSA-DE) algorithm. Finally, by means of MATLAB/Simulink tool, this cascade adjustment system of indoor temperature PIλDμplus sending air PI for an air conditioning VAV-TMN is configured and the related control effects are numerically simulated. The results show that the cascade control system is feasible in theory and the control effects is better than those of the corresponding cascade control systems of indoor temperature integer order PID plus sending air volume PI whose controller parameter values are adjusted by Ziegler-Nichols setting method and DE-algorithm, respectively.

air-conditioning variable air volume terminal (VAV-TMN); indoor temperature fractional order PID controller (IT-FOPIDC); cascade control; improved parameter self-adaptive differential evolution (IPSA-DE) algorithm; numerical simulation

1671-6612（2018）04-428-07

TU83

A

蘭州理工大學博士基金（編號：B04-237）；蘭州理工大學建工七七基金（編號：TM-QK1301）

李鵬波（1990-），男，在讀碩士研究生，E-mail：540228419@qq.com

李紹勇（1966-），男，教授，博士

2017-09-30