基于穩定性分析的動力集中動力車車輪踏面匹配研究
閆兆盈, 羅 贇, 陳國勝, 鄧小星
(1 西南交通大學 牽引動力國家重點實驗室, 成都 610031;2 大功率交流傳動電力機車國家重點實驗室, 湖南株洲 412001)
輪軌匹配關系是影響車輛動力學性能和輪軌磨耗的重要因素,選擇合適的輪軌匹配型面對提高車輛運行穩定性有重要意義。自從20世紀30年代Heumann提出磨耗型車輪踏面以來,我國的鐵路研究人員對磨耗型踏面做了大量的研究。[1]2003年3月中華人民共和國鐵道部發布了機車車輛車輪輪緣踏面外形標準,該標準取消了錐型輪緣踏面,規定了車輛車輪用踏面形狀LM,LMA和機車車輪用踏面形狀JM,JM2和JM3。[2]
黃運華等分析比較了我國LM踏面和德國DIN 5573踏面對地鐵車輛動力學性能的影響,結果表明采用DIN 5573踏面時車輛的運行穩定性優于LM踏面。[3]張劍等基于輪軌接觸幾何、非赫茲滾動接觸、車輛軌道耦合動力學計算分析了地車車輛常用的LM型踏面、S1002型車輪踏面分別與60 kg/m鋼軌匹配特性,綜合分析表明LM型踏面與60 kg/m鋼軌的接觸狀態較好。[4]劉高坤等基于某直線電機地鐵車輛分析了LM/CHN60與LMA/CHN60兩種匹配的輪軌接觸幾何及動力學性能,結果表明該地鐵車輛采用LMA踏面能獲得更好的綜合動力學性能。[5]孫善超等基于先鋒號客車基本參數建立的車輛動力學模型,分析輪軌幾何參數對高速車輛運行平穩性和穩定性的影響,研究表明:增大輪對內側距(增大等效錐度)可以改善舒適性,減小磨耗,提高臨界速度。[6]
國外學者對輪軌踏面匹配做了大量的研究,Novales和Polach等優化輪軌型面匹配參數,通過動力學仿真可知車輛動力學性能有所提高。[7]REN Z等分析比較了日本、歐洲的輪軌幾何關系差異,為高速輪軌關系的深入研究提供了基礎。[8]Shevtsov對北美貨運車輛的車輪和鋼軌滾動接觸進行模擬和試驗,測試其滾動接觸疲勞性能,進一步分析車輛運行性能。[9]
以160 km/h速度等級的動力集中動力車為研究對象,對比分析了JM3和LMA踏面與60 kg/m鋼軌匹配的運動穩定性;并基于振動模態,結合一系縱向剛度分析踏面磨耗過程中動力車穩定性的變化情況。
1 動力車計算模型
采用SIMPACK多體動力學軟件建立2B0軸式的動力車動力學模型,如圖1所示,該模型包括一個車體、兩個動力轉向架。動力車物理模型、自由度及廣義坐標參見文獻[10],車體和構架間由二系懸掛裝置連接,二系懸掛裝置由高圓彈簧(每側兩組)、兩個抗蛇行減振器、兩個橫向減振器、兩個垂向減振器構成;構架和輪對之間由一系懸掛裝置連接,一系懸掛裝置由一系彈簧、轉臂式軸箱拉桿和垂向減振器組成,驅動裝置采用彈性架懸方式。驅動裝置具有六個自由度,驅動裝置與構架懸掛座具有三向平動和轉動剛度與阻尼,擺桿相對于構架可以有兩個轉動自由度,動力車模型自由度總數為122,建模中考慮了軌枕的彈性,動力車主要參數:軸重19.5 t,軸距2.9 m,轉向架定距9.1 m,計算最高速度為210 km/h,構造速度為160 km/h。
2 新輪新軌線性穩定性計算
圖1 整車動力學模型
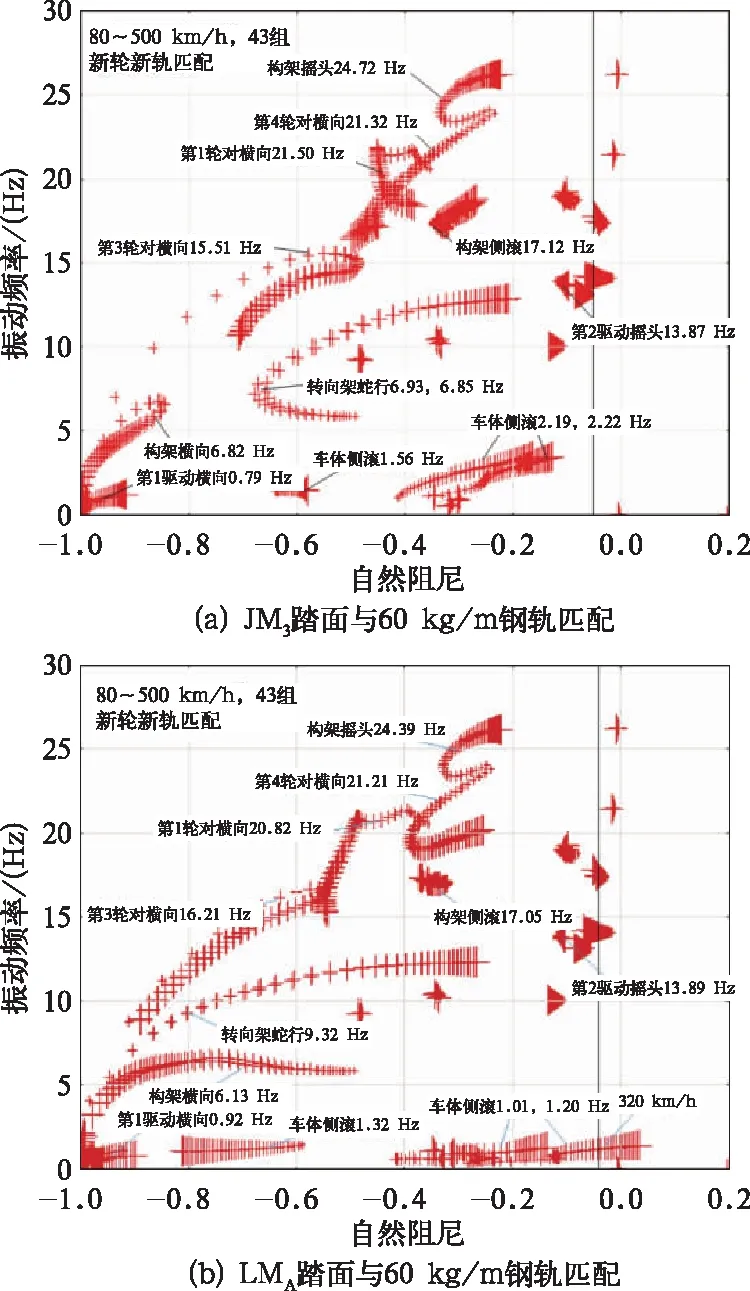
圖2 新輪新軌動力車根軌跡曲線
圖2是JM3和LMA踏面分別與60 kg/m鋼軌匹配時,進行Harmonic線性化[11]后動力車的根軌跡曲線,根軌跡曲線是指當系統中某個參量由零到無窮大變化時,其閉環特征根在平面上移動的軌跡,以橫坐標表示模態的實部(自然阻尼),縱坐標表示模態的虛部(振動頻率Hz),[12]變化的參數是速度從80~500 km/h,速度增量為10 km/h,故圖中每一條根軌跡曲線都是由43個“+”號組成,且隨著速度的增加,“+”號的形狀也變大。圖中還給出了速度160 km/h時,各主要剛體的振動頻率。理論上,當系統的所有特征根實部全為負值時,系統的運動是穩定的。實際上,在機車車輛應用領域,阻尼很小時系統的平穩性將受到影響,考慮到安全裕量問題,當自然阻尼即橫坐標超過-5%時,即判定出現蛇行運動失穩。
圖2中每一條根軌跡都是動力車模型中一個振動模態隨速度變化的軌跡。隨著速度的提高,變化甚微的模態對應的頻率是剛體的固有振動頻率,其中有多個模態的阻尼隨速度的提高而減小。
一系縱向剛度為15 MN/m,采用JM3踏面時,在最高速度下最危險模態的自然阻尼為負,而且阻尼比較大,動力車穩定性非常高,線性臨界速度大于500 km/h;采用LMA踏面時,失穩模態是車體側滾,臨界速度為320 km/h。
LMA踏面與60 kg/m鋼軌匹配時(軌底坡1/30),在輪對橫移量y<6 mm時等效錐度約0.033。而JM3踏面的等效錐度約0.117。兩種匹配關系在160 km/h運行速度下車體側滾、轉向架蛇行、輪對橫向的頻率及車體側滾的阻尼差別較大,隨著速度的增大同一振型模態的變化趨勢也不同。
3 新輪新軌非線性穩定性計算
在計算動力車非線性穩定性時,截取一段長度為50 m的AAR5級不平順時域譜作為激擾,動力車以一定速度通過不平順后,在無不平順直道上繼續運行到300 m時,考察第一輪對橫向振動位移的收斂和發散情況來判斷其穩定性,結果見圖4。計算結果表明,采用JM3動力車的蛇行失穩臨界速度為340 km/h;采用LMA踏面為160 km/h,通過調整動力車參數(抗蛇行減振器卸荷阻力,卸荷速度及關節剛度)也不能達到臨界速度快速提高的效果。
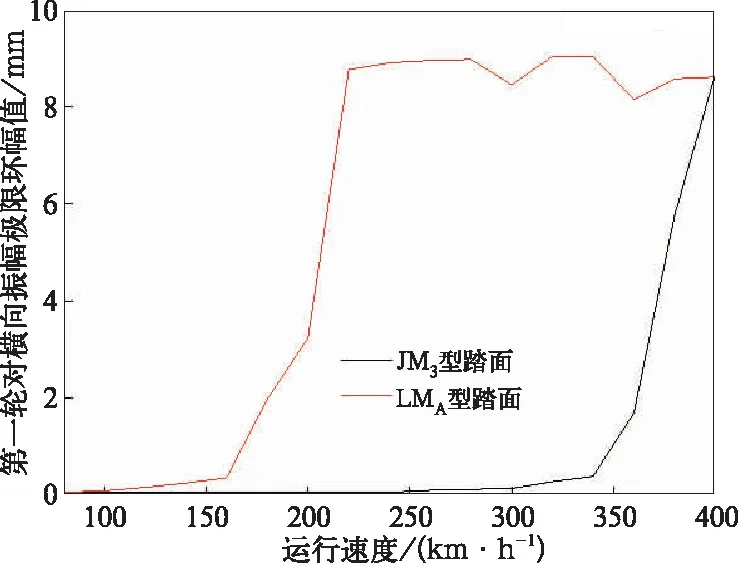
圖3 非線性臨界速度計算結果
4 等效錐度對整車線性穩定性的影響
4.1 臨界速度計算
以下計算采用JM3踏面進行Equivalent線性化[11]。通過根軌跡法計算分析一系縱向剛度的大小在不同等效錐度下對動力車穩定性的影響。計算結果見表1,在整個服役過程中,隨著等效錐度的變化,動力車也能保證160 km/h運行時的運動穩定性。
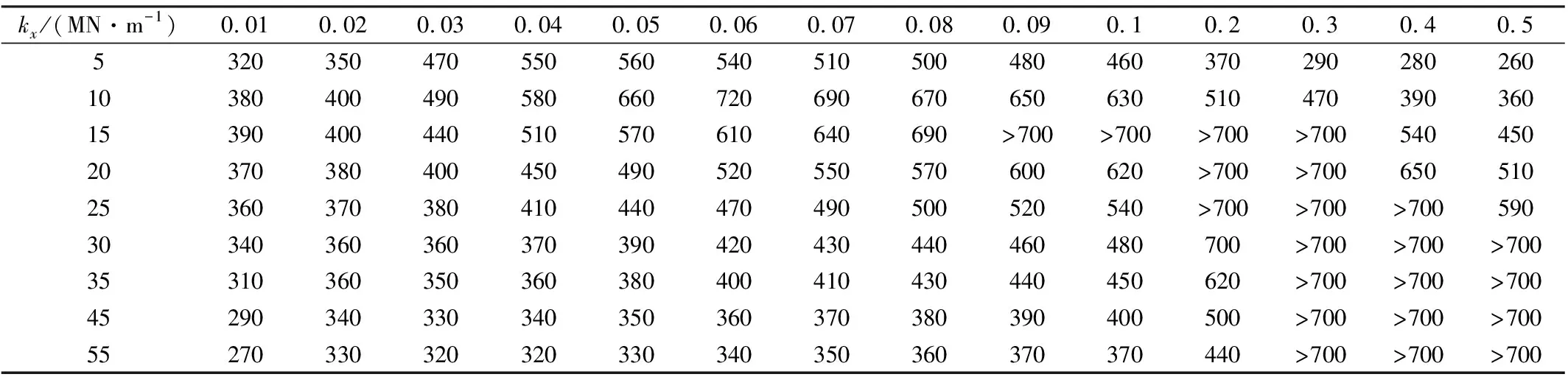
表1 等效錐度λ與一系縱向剛度kx對臨界速度vcr(km/h)的影響
從計算結果來看,臨界速度隨著等效錐度的增大先增后減;在不同的一系縱向剛度下,出現臨界速度最大值的等效錐度值隨著剛度增大而增大。
在相同等效錐度下,臨界速度隨著一系縱向剛度增加而先增大,當一系縱向剛度超過某一分界后,臨界速度逐漸減小,隨著剛度增加對其影響程度變緩。當一系縱向剛度為5 ~10 MN/m時,大錐度下的臨界速度較低,當一系縱向剛度大于35 MN/m時,在小錐度下臨界速度較低。所以該動力車一系縱向剛度可取15~30 MN/m,在該范圍內,當車輪踏面從JM3新輪開始,磨耗到限(等效錐度為0.5)過程中,不同等效錐度下動力車穩定性均好。由于沒有車輪磨耗到限的踏面外形,無法計算相應的非線性臨界速度,從錐度為0.033和0.117 的線性臨界速度是非線性臨界速度的兩倍多關系,可以推斷在車輪磨耗到限過程中,動力車非線性穩定性可以滿足160 km/h的運行要求。
4.2 等效錐度變化引起整車失穩危險模態分析
一系縱向剛度取5 MN/m,等效錐度0.01和0.1時的振動模態以及一系縱向剛度取15 MN/m,等效錐度0.1和0.5時的振動模態如圖4,每個模態的計算速度范圍為80~570 km/h,步長10 km/h。
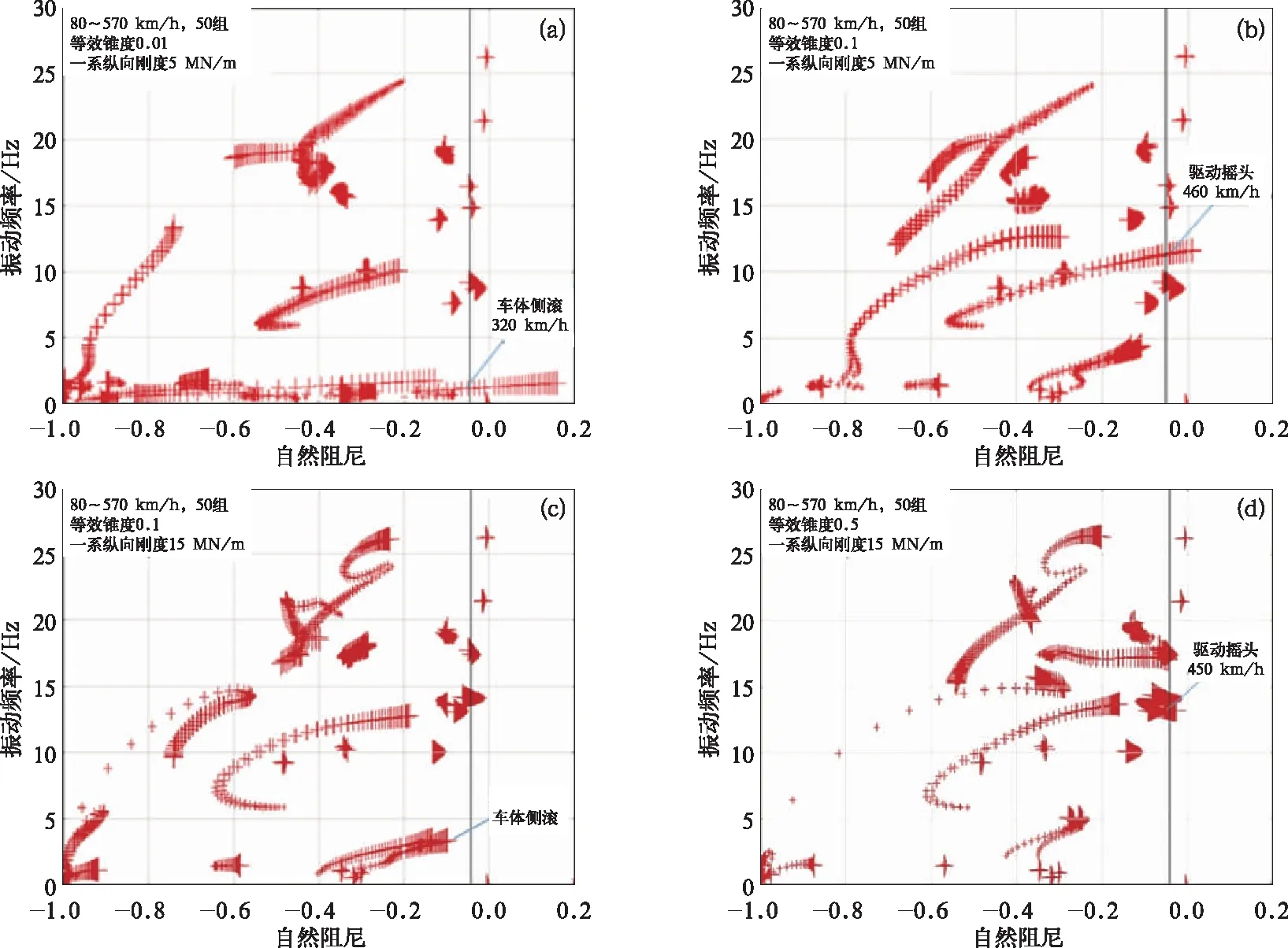
圖4 不同等效錐度下的振型模態
由圖4根軌跡曲線中振型模態的變化可知:隨著等效錐度的增大,各振型模態的頻率和阻尼發生變化。從振型模態的變化趨勢可以看出,在小錐度時整車蛇行失穩是由車體側滾引起的,且隨著等效錐度增加,穩定性逐漸提高,等效錐度對車體失穩模態的頻率和阻尼影響減緩;當臨界速度達到最大時,引起蛇行失穩的振動模態發生變化,此后驅動搖頭導致蛇行運動失穩,且隨著等效錐度增大,穩定性逐漸減小;一系縱向剛度5 MN/m時,等效錐度大于0.1后,對驅動模態的阻尼有顯著的影響,穩定性迅速下降;一系縱向剛度15 MN/m時,等效錐度大于0.1后,對驅動模態阻尼的影響微小,穩定性下降緩慢。
5 結 論
通過JM3和LMA踏面分別與60 kg/m鋼軌匹配的160 km/h速度等級動力集中動力車穩定性計算,以及等效錐度和一系縱向剛度對動力車穩定性的影響分析,可以得到如下結論:
(1)采用JM3踏面動力車的線性穩定性比LMA踏面高;兩種踏面下動力車的非線性臨界速度分別為340 km/h和160 km/h。
(2) 隨著等效錐度從0.01增大到0.5,動力車的線性臨界速度先增大后減小。其原因是在小錐度時失穩模態為車體側滾,隨等效錐度增大穩定性逐漸提高;當達到某一錐度時,整車失穩模態變為驅動搖頭,且隨等效錐度增大穩定性下降。
(3)一系縱向剛度在15~30 MN/m,當車輪踏面從JM3新輪開始,磨耗到限(等效錐度為0.5)過程中,不同等效錐度下動力車穩定性均滿足設計要求。

