改進的快速遺傳算法在函數優化中的應用

周勇 胡中功

摘 要： 遺傳算法作為一種模仿生物自然進化過程的全局隨機優化算法，在工程中已得到廣泛應用。但普通遺傳算法易存在早熟及收斂速度慢等缺點。提出一種快速收斂的改進遺傳算法，該算法從全局出發，對初始群體生成、遺傳選擇、交叉和變異算子操作等幾個方面做出改進，其中重點對交叉率和變異率進行優化，實現交叉率和變異率按個體適應度以S曲線和高斯分布曲線形式進行非線性自適應調整。通過案例仿真分析，證明了該方法的可行性和有效性，且具有更快的收斂速度和更可靠的穩定性。

關鍵詞： 遺傳算法； 高斯分布； 自適應； 收斂； 性能仿真； 函數優化

中圖分類號： TN911.1?34； TP18 文獻標識碼： A 文章編號： 1004?373X（2018）17?0153?05

Abstract： Genetic algorithm （GA）， as a global stochastic optimization algorithm to simulate the natural evolution process of biology， has been widely used in engineering field， but the common GA has slow convergence speed and is easy to fall into premature convergence. Therefore， an improved fast?convergence GA is proposed to improve the items of initial population generation， genetic selection， operators crossover and operators mutation proceeding from the overall situation. The crossover rate and mutation rate are optimized emphatically to realize the nonlinear adaptive adjustment in the forms of the S curve and Gaussian distribution curve according to individual fitness. The analysis results of case simulation show that the method is feasible and effective， and has fast convergence speed and high stability.

Keywords： genetic algorithm； Gaussian distribution； adaptation； convergence； performance simulation； function optimization

0 引 言

遺傳算法（Genetic Algorithm，GA）是美國Holland教授于1975年首先提出來的一種借鑒生物進化理論和門德爾基因遺傳理論的高度并行、隨機的優化方法[1]。它模擬自然界生物“優勝劣汰，適者生存”的自然進化過程，將研究的解空間映射為遺傳空間[2]，主要特點是整體搜索策略和優化搜索方法在計算時不依賴于梯度信息或其他輔助知識，也不依賴于問題的具體領域[3]。近年來，從簡單的PID控制，到復雜的最優控制、自適應控制等遺傳算法在各種工程控制問題中都有成功的應用案例。特別是目前人工智能的蓬勃發展，因而極具潛力的遺傳算法一直是研究的熱點。遺傳算法雖然應用廣泛，但在解決復雜問題時，由于其自身的隨機搜索特點也帶來了收斂速度慢和算法局部收斂（早熟）等問題[4]。遺傳算法的交叉率[Pc]和變異率[Pm]反映了算法交叉和變異操作的概率，直接影響算法的收斂性能。標準（基本）遺傳算法（SGA）的交叉率和變異率這兩個參數是固定的，導致收斂能力和穩定性較差。文獻[5?8]對遺傳算法做了一些改進。文獻[5]提出一種根據適應度調整交叉率和變異率的自適應遺傳算法（AGA），但在該算法中，個體適應度越高，平均適應度和最大適應度越接近，交叉率和變異率不斷變小并接近于0，導致在進化初期，種群中的優良個體幾乎不會改變，使算法搜索性能下降。文獻[6]中的改進遺傳算法（線性自適應遺傳算法LAGA）解決了算法初期交叉率和變異率為零的不足，但在算法后期，當種群平均適應度和最大適應度接近時，交叉率和變異率自適應調整曲線變化比較陡峭，產生較大差異，使進化停滯不前，產生局部收斂的可能。文獻[7]把交叉和變異率按個體適應度以Sigmoid函數曲線非線性自適應調整，但進化初期變異率過大，雖能增加種群多樣性，但可能使算法收斂速度變慢。文獻[8]提出一種新的交叉和變異算子，但算法交叉率和變異率是固定的，增加了產生早熟的概率。針對遺傳算法存在的不足，本文提出一種改進的快速遺傳算法（IFGA），該算法從全局出發，分別對初始化分配、選擇、交叉和變異等幾個方面進行改進，其中著重從交叉和變異改進的方向出發，自適應地以非線性曲線模式優化交叉概率和變異概率，滿足算法對不同階段的側重，以增加種群多樣性，提高算法搜索能力和收斂速度。復雜函數的仿真實驗結果表明，改進的遺傳算法能較好地解決傳統遺傳算法存在的不足，改善收斂性質。

1 改進的遺傳算法基本原理

1.1 初始群體生成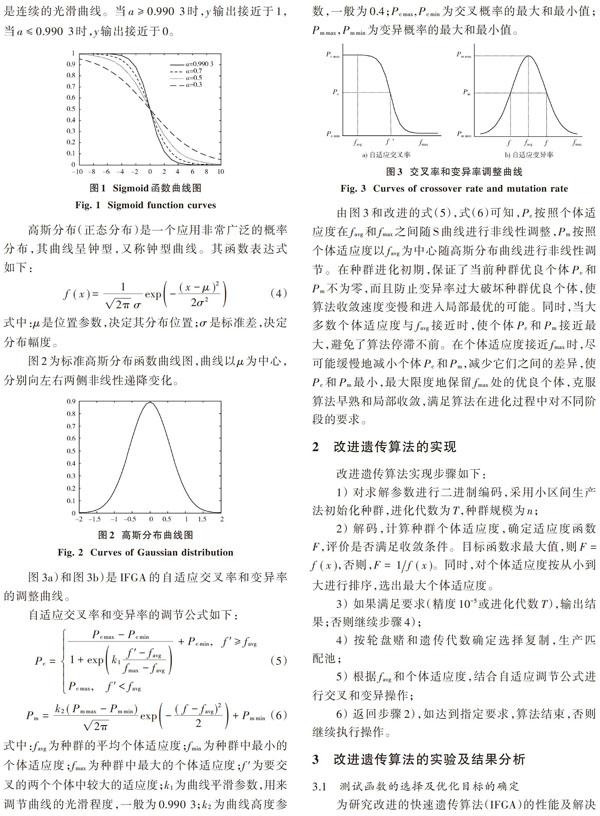

初始群體的分布對算法的收斂有較大影響。初始群體分布不合理會導致算法收斂速度變慢，特別當遺傳算子選擇不當時，甚至早熟不收斂。基本（標準）遺傳算法和大部分遺傳算法的初始群體在搜索空間都是隨機產生的，這種方法可能使解空間個體都集中在某一局部區域內，這對搜索全局最優點極為不利。本文針對常規初始群體存在的問題，借鑒文獻[9]提出的小區間初始群體生產法，將規模為[n]的群體[E]以待求參數的取值范圍分成群體總數個小區間，并在各小區間中分別隨機產生一個初始個體，從而保證初始個體能均勻地分布在整個解空間范圍內，增強初始群體的活力。

1.2 選擇操作的改進

選擇操作反映了“優勝劣汰，適者生存”的自然界規律，它以個體的適應度作為衡量標準，適應度高的個體作為父代被選擇繁衍進入下一代進化；反之，則被淘汰。選擇策略比較多，經典遺傳算法常采用輪盤賭選擇方式。輪盤賭選擇方式根據個體適應度值在群體適應度總和中所占的比例來表示其被選中的概率，適應度越高的個體，被選中的幾率越大。但這種選擇方式的選擇誤差較大，對收斂速度有較大影響。為了豐富種群模式，優化算法收斂性質，本文中選擇算子采用輪盤賭方式和遺傳代數相結合自適應調整選擇概率。改進后的選擇算子為：

式中：[fE（1，i）i=1nfE（1，i）]為輪盤賭方式的初代選擇算子；[T]為最大進化代數；[k]為實數，一般為8～10。

從式（2）可知，算法在進化初期根據輪盤賭方式進行遺傳操作，使子代群體模式豐富，降低了早熟的可能性。在進化后期，隨著進化代數的增加，加大了選擇算子的概率，可極大地促進種群中適應度較高的個體進行進化操作，能夠較好地提高算法的收斂速度。

1.3 自適應交叉率和變異率的改進

遺傳算法中，交叉和變異算子是算法進化的核心，對算法收斂性和穩定性有重要作用。交叉算子通過基因重組獲取優良個體，決定了遺傳算法的全局搜索能力[10]。變異算子通過改變群體個體基因，保證算法能搜索到解空間中的任何角落，能夠較好地維持群體的多樣性，克服早熟，使算法具有全局收斂性。遺傳算法的交叉率和變異率是算法收斂、穩定的關鍵參數。交叉率越大，算法搜索空間越大，種群越豐富，產生新個體的速度越快，但是優良個體破壞的可能性越大；交叉率過小，不易產生新個體，使得搜索過程緩慢。變異概率是全局最優解的關鍵，變異率越小，不容易產生新的個體結構，種群多樣性變差；變異率過大，又會使遺傳算法變成純粹的隨機搜索算法[6]。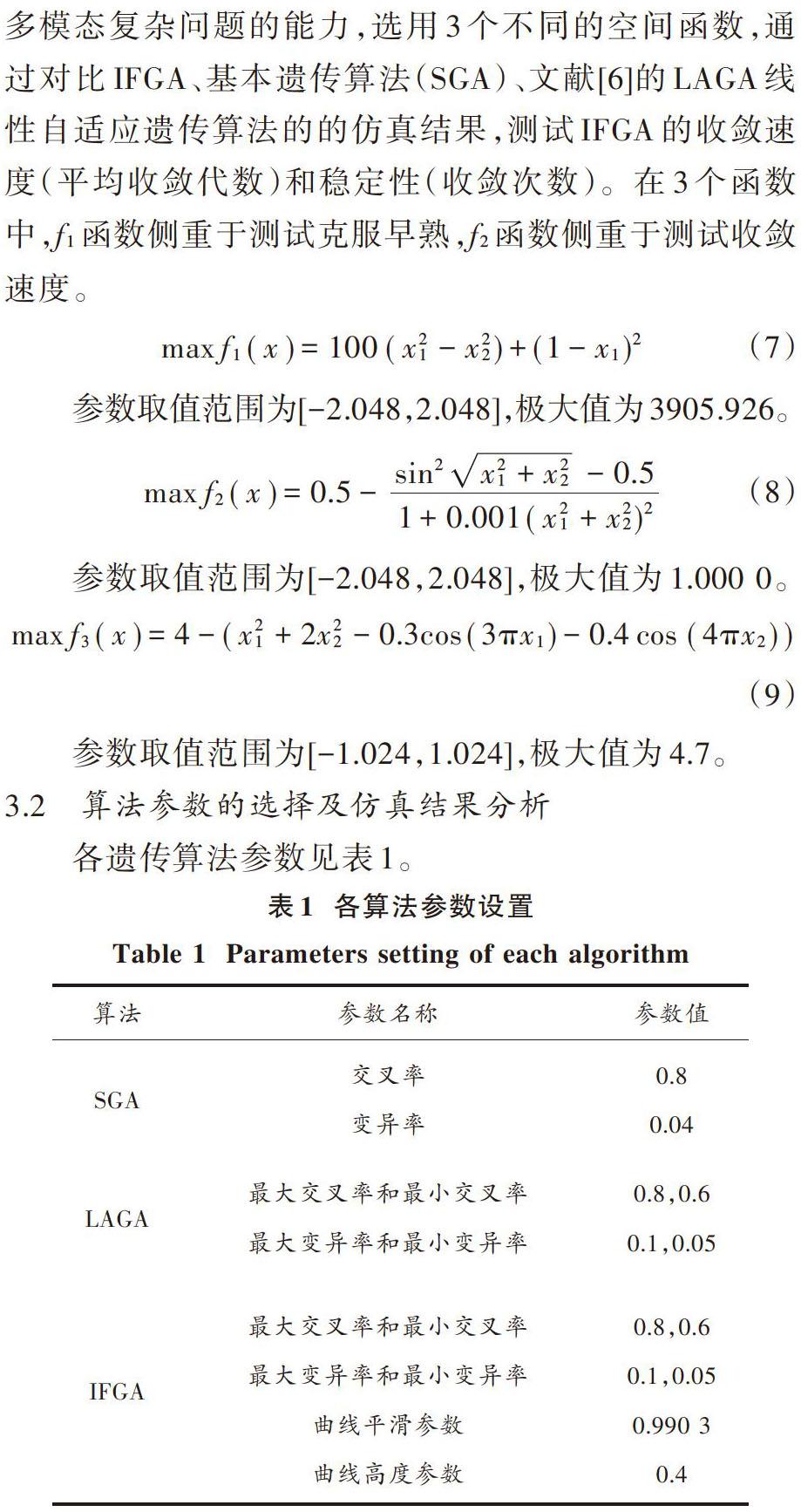

本文基于Sigmoid函數和高斯分布函數對交叉率和變異率進行改進，設計自適應非線性調整交叉率和變異率的調節公式。改進算法解決以下幾個問題：

1） 在進化初期，要提高搜索速度和個體多樣性，而且保證種群中最優個體的交叉率和變異率不應為零；

2） 當平均適應度和最大適應度相差較大時，不會出現線性調整，避免進化停滯不前；

3） 算法后期，在滿足精度的情況下，使接近最大適應度處曲線更光滑，緩慢減小交叉率和變異率，使交叉率和變異率的差異減小，較好地保留優良個體。

由圖3和改進的式（5），式（6）可知，[Pc]按照個體適應度在[favg]和[fmax]之間隨S曲線進行非線性調整，[Pm]按照個體適應度以[favg]為中心隨高斯分布曲線進行非線性調節。在種群進化初期，保證了當前種群優良個體[Pc]和[Pm]不為零，而且防止變異率過大破壞種群優良個體，使算法收斂速度變慢和進入局部最優的可能。同時，當大多數個體適應度與[favg]接近時，使個體[Pc]和[Pm]接近最大，避免了算法停滯不前。在個體適應度接近[fmax]時，盡可能緩慢地減小個體[Pc]和[Pm]，減少它們之間的差異，使[Pc]和[Pm]最小，最大限度地保留[fmax]處的優良個體，克服算法早熟和局部收斂，滿足算法在進化過程中對不同階段的要求。

2 改進遺傳算法的實現

改進遺傳算法實現步驟如下：

1） 對求解參數進行二進制編碼，采用小區間生產法初始化種群，進化代數為[T]，種群規模為[n]；

2） 解碼，計算種群個體適應度，確定適應度函數[F]，評價是否滿足收斂條件。目標函數求最大值，則[F=f（x）]，否則，[F=1f（x）]。同時，對個體適應度按從小到大進行排序，選出最大個體適應度。

3） 如果滿足要求（精度10-5或進化代數[T]），輸出結果；否則繼續步驟4）；

4） 按輪盤賭和遺傳代數確定選擇復制，生產匹配池；

5） 根據[favg]和個體適應度，結合自適應調節公式進行交叉和變異操作；

6） 返回步驟2），如達到指定要求，算法結束，否則繼續執行操作。

3 改進遺傳算法的實驗及結果分析

3.1 測試函數的選擇及優化目標的確定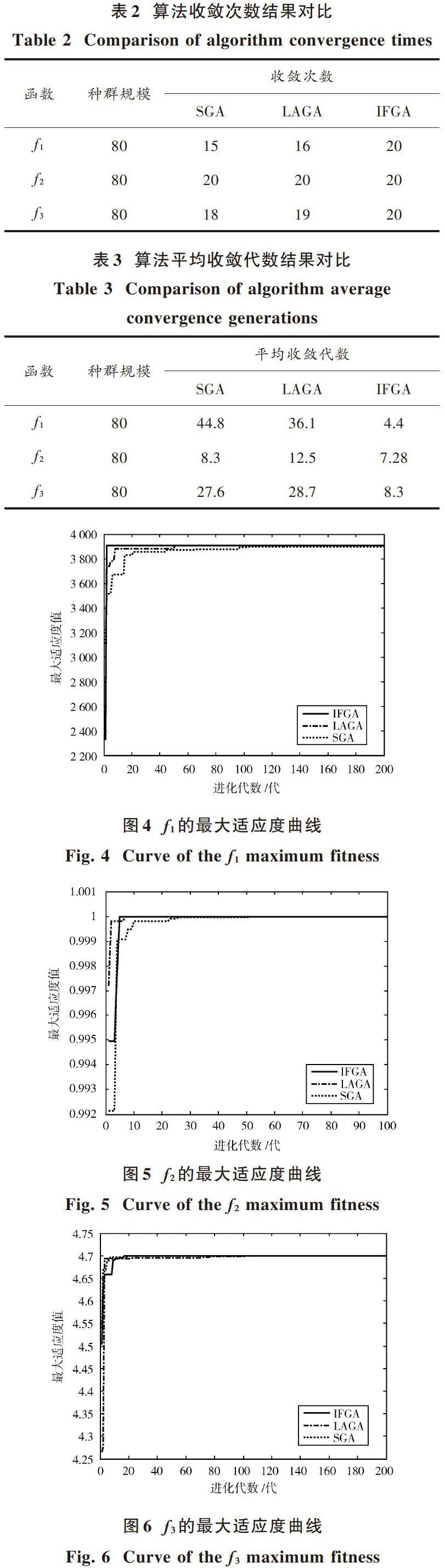

為研究改進的快速遺傳算法（IFGA）的性能及解決多模態復雜問題的能力，選用3個不同的空間函數，通過對比IFGA、基本遺傳算法（SGA）、文獻[6]的LAGA線性自適應遺傳算法的的仿真結果，測試IFGA的收斂速度（平均收斂代數）和穩定性（收斂次數）。在3個函數中，[f1]函數側重于測試克服早熟，[f2]函數側重于測試收斂速度。

3.2 算法參數的選擇及仿真結果分析

各遺傳算法參數見表1。

選擇[f1，f3]的最大進化代數為200代，[f2]的最大進化代數為100代。3種遺傳算法均采用二進制編碼，交叉操作采用單點交叉，變異操作采用基本位變異，SGA和LAGA采用經典輪盤賭選擇策略。

由于遺傳算法中存在大量隨機操作，因此對每種算法各運行20次，統計最優解的收斂次數和平均收斂代數。各算法測試結果見表2和表3，以及圖4～圖6。

從表2和表3看出，對[f1]函數，SGA的平均收斂代數是本文算法的10.18倍，LAGA平均收斂代數是本文算法的8.2倍，同時，SGA未收斂5次，LAGA未收斂4次，IFGA無未收斂情況。對[f2]函數，SGA和LAGA的平均收斂代數比本文算法多1.02次和5.22次。而對[f3]函數，SGA和LAGA的平均收斂代數比本文算法多19.3次和20.4次。可見，IFGA無論在收斂性還是穩定性上均極大地改善了遺傳算法的性能。

圖4～圖6為在3個測試函數下IFGA，SGA和LAGA搜索最大適應度值的對比曲線。從圖4～圖6可看出，SGA和LAGA在進化初期容易出現停滯現象。當種群大部分個體接近平均適應度時，由于SGA采用固定的[Pc]和[Pm]，很難跳出局部收斂，雖然LAGA采用了線性自適應調節[Pc]和[Pm]，可以跳出局部收斂的不利狀態，但是拖慢了其收斂速度。相比之下，本文提出的改進遺傳算法能較好地適應外部環境，當SGA和LAGA在進化初期處于停滯階段時，IFGA將接近平均適應度的相近個體進行大交叉和變異操作，呈階梯上升趨勢，以最快速度擺脫局部收斂，具有較好的收斂速度和穩定性。

4 結 語

本文針對傳統和改進遺傳算法在收斂性和穩定性上的不足，提出一種改進的遺傳算法。算法從全局出發，對初始化分配、選擇、交叉和變異等幾個方面進行改進。其中，結合S型曲線和高斯分布曲線，著重對交叉率和變異率的自適應調節進行設計。在求解函數優化問題時，改進的遺傳算法無論在收斂速度還是穩定性上，都比SGA和LAGA等遺傳算法有較明顯的優勢，克服了遺傳算法易陷入早熟和收斂速度慢等問題。因此，本文提出的改進遺傳算法是有效的，為實際工程應用提供了理論支持。

參考文獻

[1] 余有明，劉玉樹，閻光偉.遺傳算法的編碼理論與應用[J].計算機工程與應用，2006，42（3）：86?89.

YU Youming， LIU Yushu， YAN Guangwei. Encoding theory and application of genetic algorithm [J]. Computer engineering and applications， 2006， 42（3）： 86?89.

[2] 程敏，宋宇博，孫剛，等.改進的自適應遺傳算法及其性能研究[J].計算機與數字工程，2014，42（3）：355?358.

CHENG Min， SONG Yubo， SUN Gang， et al. An improved self?adaption genetic algorithm and its performances [J]. Computer and digital engineering， 2014， 42（3）： 355?358.

[3] LINDA M M， NAIR N E. A new?fangled adaptive mutation breeder genetic optimization of global multi?machine power system stabilize [J]. International journal of electrical power and energy systems， 2013， 44（1）： 249?258.

[4] XU Haiyan. Research for new modified adaptive genetic algorithm [C]// 2012 IEEE World Automation Congress. Puerto Vallarta： IEEE， 2012： 146?147.

[5] SRINVAS M， PATNAIK L M. Adaptive probabilities of crossover and， mutation in genetic algorithms [J]. IEEE transactions on system man and cybernetics， 2002， 24（4）： 656?667.

[6] 任子武，傘冶.自適應遺傳算法的改進及在系統辨識中應用研究[J].系統仿真學報，2006，18（1）：41?43.

REN Ziwu， SAN Ye. Improved adaptive genetic algorithm and its application research in parameter identification [J]. Journal of system simulation， 2006， 18（1）： 41?43.

[7] 金立兵，胡穎，祁繼鵬.改進的自適應遺傳算法在結構優化設計中的應用[J].信陽師范學院學報（自然科學版），2016，29（4）：621?624.

JIN Libing， HU Ying， QI Jipeng. Application of improved adaptive genetic algorithm in structural optimization design [J]. Journal of Xinyang Teachers College （natural science edition）， 2016， 29（4）： 621?624.

[8] 謝燕麗，許青林，姜文超.一種基于交叉和變異算子改進的遺傳算法研究[J].計算機技術與發展，2014，24（4）：80?83.

XIE Yanli， XU Qinglin， JIANG Wenchao. An improved genetic algorithm based on crossover and mutation operators [J]. Computer technology and development， 2014， 24（4）： 80?83.

[9] 高瑋.改進的快速遺傳算法及其性能研究[J].系統工程與電子技術，2003，25（11）：1427?1430.

GAO Wei. An improved fast?convergent genetic algorithm and its performance study [J]. Systems engineering and electronics， 2003， 25（11）： 1427?1430.

[10] 楊從銳，錢謙，王鋒，等.改進的自適應遺傳算法在函數優化中的應用[J].計算機應用研究，2018，35（4）：1042?1045.

YANG Congrui， QIAN Qian， WANG Feng， et al. Application of improved adaptive genetic algorithm in function optimization [J]. Application research of computers， 2018， 35（4）： 1042?1045.

[11] 梅俊偉，彭仕宓，李雄炎，等.利用Sigmoid函數表征超低滲透儲層的非達西滲流特征[J].西安石油大學學報（自然科學版），2011，26（2）：64?67.

MEI Junwei， PENG Shimi， LI Xiongyan， et al. Characterization of the non?darcy seepage flow in ultra?low permeability reservoir based on Sigmoid function [J]. Journal of Xian Shiyou University （natural science edition）， 2011， 26（2）： 64?67.