地鐵車輛牽引電機矢量控制的研究與應用

湖南磁浮交通發展股份有限公司 石 碩

隨著城市規模不斷擴大，人們出行與交通擁堵的矛盾日益凸顯。地鐵由于運量大、準時、速度快、節省地面空間、節約能源等特點，成為緩解城市交通壓力的一種有效手段。同時，公眾對地鐵運營速度、載客能力提出了更高的要求，車輛牽引系統設備也逐步升級以提高車輛平均旅行速度、最大運行速度。本文提出采用矢量控制對交流異步牽引電機轉矩控制進行調速，優化車輛牽引特性；分析了交流異步電機的空間矢量等效變換、dq坐標系變換、MT旋轉坐標軸同步，推導矢量控制數學模型；結合地鐵車輛牽引系統仿真牽引電機矢量控制的性能。

1 矢量控制數學模型

1971年，德國學者Blaschke提出了交流電動機矢量控制理論，它的出現對電機技術的研究具有里程碑的意義[1]。矢量控制是電機磁場定向控制實現瞬時轉矩的控制方法，通過適當的坐標變換將定子電流矢量分解為勵磁電流分量和轉矩電流分量，把交流量控制變化為直流量控制，等同于直流電機。

1.1 空間法平面

將某些在空間按正弦分步的物理量用空間矢量表示。以三相感應電機感應電動機與轉軸垂直的空間斷面作為空間復平面表示電機內部空間矢量。

在電動機復平面內，取空間靜止復坐標（Re-Im），以實軸為空間坐標參考軸，空間中任一矢量R可表示為R=∣R∣ejθ，∣R∣為矢量的模，θ為矢量軸線與參考軸的空間電角度，稱為空間相位[2]。

三項繞柱軸線ABC構成空間三相軸系，ABC軸系在空間復平面的位置，A相繞組軸線與Re空間電角度來確定，取A軸與Re軸重合，B軸的空間電角度為α= ej120o，B軸的空間電角度為α2= ej240o。

定子三相繞組通電后分別產生沿著各自繞組軸線脈動的空間磁動勢fA、fB、fC，各自以ABC軸沿圓周正弦分布的空間矢量，其幅值為FA(t)、FB(t)、FC(t)是變化的，取決于相電流的瞬時值。三相基波合成的磁動勢為fs，即：

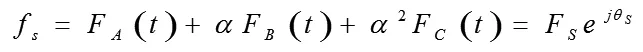
式中，fs為空間矢量；其幅值為Fs。

定子電流可以是任意波形和任意時刻的瞬時值，其流入繞組產生的磁動勢在空間按正弦分布，fS是三相電流通過繞組共同作用的結果。當電流變化時，fS的幅值和相位都在變化。同時，其旋轉軌跡為圓形，半徑為每相基波磁動勢最大幅值3/2倍，矢量旋轉的電角度ωS就是電流角頻率，旋轉方向是從A軸到B軸再到C軸。當時間參考軸與復平面的實軸重合時，fS的空間相位與A軸電流的時間相位相同。A相電流最大時，fS的與A軸重合，B相和C相亦然。

在復平面上不但可以用空間矢量表示定子繞組的電壓、電流、磁動勢以及其合成矢量，也可以表示轉子繞組的相應參數。

1.2 ABC軸系到dq軸系的坐標變換

將空間復平面的實軸Re定為d軸，虛軸Im為q軸，構成dq軸系，空間矢量f采用dq軸系表示為f d、f q。用DQ和dq繞組分別取代原來的定子、轉子三相繞組[3]。

1.3 同步旋轉MT軸系坐標變換

MT軸系是以同步角速度在空間旋轉的正交坐標系。在圖1中，各空間矢量在同步坐標系內正交變換。is是ABC軸系中電機實際產生的空間矢量，這是單軸復矢量。在正弦穩態下，is在MT軸系中為直流量，變換后的iM和iT也為直流量。MT軸上的磁動勢矢量fM和fT不再是脈動的，而是固定不變的，其幅值和方向取決于相電流的有效值、A相電流相位初始角和MT軸系初始位置角。磁動勢矢量相對MT軸是靜止的，但依靠MT軸的旋轉，成為同步旋轉的原型磁動勢。通過控制iM和iT即可控制is。在動態情況下，仍可通過iM和iT控制is的幅值和相位。

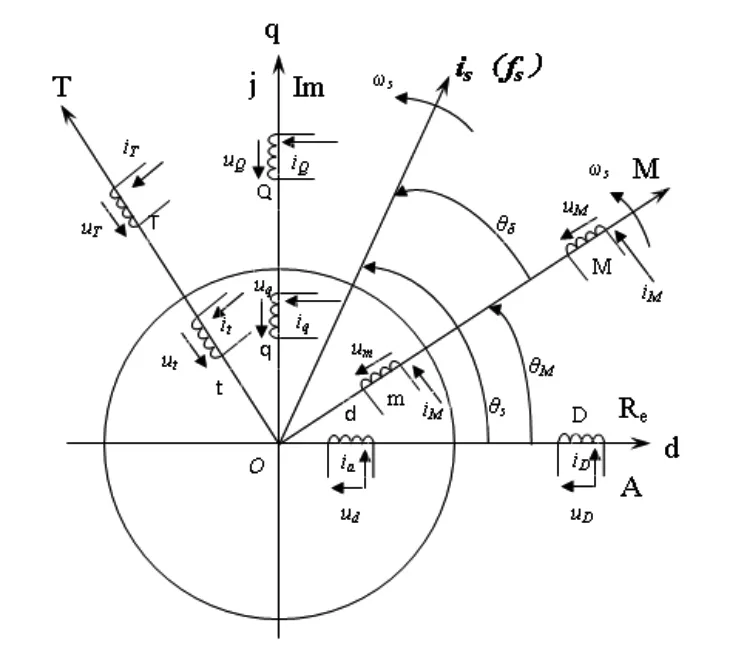
圖1 靜止dq軸系到同步旋轉MT軸系的矢量變換

矢量變換控制的數學模型為：

式中uM、uT為定子電壓歸算到MT軸的分量；um、ut為轉子電壓歸算到MT軸的分量；iM、iT為定子電流歸算到MT軸的分量；im、it為轉子電流歸算到MT軸的的分量。

矢量變換對電壓、電流的波形沒有限制，不僅適用穩態分析與控制，也適用于動態分析與控制。

2 牽引電機矢量控制特性仿真計算

車輛牽引電機工作性仿真計算是對列車牽引和運行特性的理論驗證，為牽引系統設計、電機及其控制算法提供理論依據，證明牽引性能滿足實際需要。同時，通過牽引特性仿真計算可以優化牽引控制，也為供電、信號、軌道等系統設計提供的車輛邊界條件。牽引電機參數如表1。

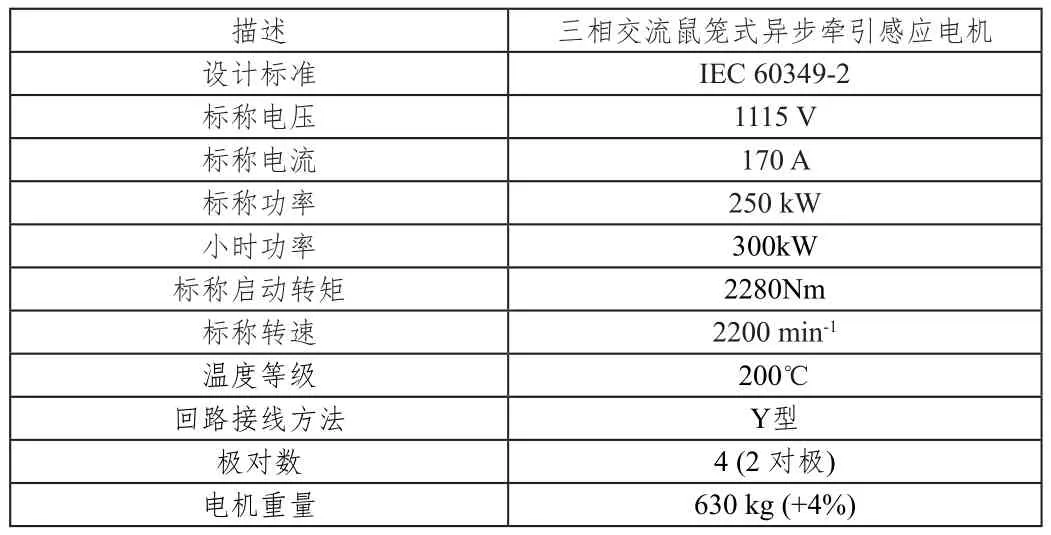
表1 電機參數

圖2 仿真初始條件設置

對基于矢量控制的列車牽引系統的特性進行計算，仿真初始條件為圖2所示。

牽引電機仿真結果，電機最大滑差率s=13%，滑差率隨電機轉速升高逐步降低；恒轉矩輸出為2200Nm，恒轉矩轉速區域為0-1400rpm，電流基波有效值為305A；最小轉矩為550Nm轉速為3750rpm，電流基波有效值為140A；最大工作頻率為128Hz，轉速為3750rpm；電機最大電壓基波有效值為1080V；電機最高效率為94%。

3 結論

本文在分析電機矢量控制基本原理和數學模型的基礎上，對地鐵車輛牽引電機矢量控制進行仿真，通過分析得到以下結論：

（1）異步電機矢量控制方法解耦了電機勵磁和轉矩，可提高動態性能。

（2）矢量控制實現電機恒轉矩、恒功率、弱磁三階段調速。增大電機恒轉矩、恒功率運行區域，在高轉速情況下保證電機效率，弱磁調速階段優化轉矩輸出。

（3）電機參數以及在運行中的變化情況，將直接影響到磁場定向的準確性，同時電源低次諧波電流將產生轉矩脈動，并造成轉速脈動，這些問題將決定矢量控制的性能。矢量控制必須基于精準的電機及電源模型的前提下完成。