渦流發生器對不同弦長風力機翼型氣動性能的影響

龔玉祥，周曉亮，程明哲

(浙江運達風電股份有限公司，風力發電系統國家重點實驗室，浙江 杭州 310012)

風力機葉片的大型化趨勢使得葉片長度越來越長，為了保證葉片根部的強度，葉片的結構設計上大多選用大厚度的翼型，這就導致了在大攻角下，大厚度的翼型更加容易發生氣動分離現象，導致葉片吸收風能的能力降低，從而降低了風輪效率[1]；因此，控制流動分離和減小葉片阻力成為風力機氣動研究領域的熱門問題之一。

1947年，美國聯合飛機公司的Bmynes和Taylor首次提出了將渦流發生器(VGs)應用于推遲飛機機翼的邊界層分離[2]。VGs 安裝在葉片上表面邊界層內，并與當地來流保持一定的側向夾角。VGs產生的尾渦擾動分離區內的氣流，使邊界層上部高能氣流與近壁低能氣流混合，增加近壁流體的動量和能量，延緩分離，同時VGs 技術安裝工藝簡單，經濟性高；因此，被應用于大型風力機上[3-4]。Lin通過風洞試驗和數值模擬，得到了渦流發生器安裝位置應該離分離點較近的結論[5]。Johansen等在數值計算中將渦流發生器兩側的邊界層條件設為對稱邊界及周期性邊界，研究了VGs 對風力機葉片氣動性能的影響規律[6]。張磊等采用CFD方法分析了VGs對風力機專用翼型DU 91-W2-250氣動性能的影響規律，對比了14°攻角下光滑翼型和VGs 翼型的流動特性，揭示了VGs對翼型的流動控制機制[7]。趙振宙等考慮了轉捩效應的影響，采用SST全湍流模型和Gamma-Theta轉捩模型對翼型DU 91-W2-250進行了數值模擬，研究結果表明轉捩模型計算結果較試驗值更加吻合[8-9]。

在翼型上安裝渦流發生器的研究中使用的翼型弦長大都為0.6 m，而實際風力機葉片的厚翼型截面對應的弦長可達4 m[10]；因此，本文在不改變渦流發生器尺寸和安裝位置的情況下，研究了弦長變化對翼型氣動特性的影響規律。

1 計算模型

1.1 幾何模型和網格劃分

翼型選用DU系列風力機專用翼型DU97-W2-300為研究對象，此翼型試驗模型弦長為0.6 m，裝有VGs的試驗數據由荷蘭Delft大學通過風洞實驗得到[11]，可驗證數值計算方法的可靠性，模型如圖1所示。

圖1 幾何模型

計算段翼型的展向長度與試驗模型保持一致，長度為0.175 m，計算弦長分別為0.6 、1和1.5 m，在翼型弦長20%處共安裝5組VGs，具體幾何尺寸如圖2所示。VGs的形狀為三角形，其弦向有效長度為17 mm，高度5 mm，攻角為16.4°，每組內的兩個三角形葉尖距離為10 mm，相鄰的兩組VGs的排列周期為35 mm。

采用ANSYS ICEM劃分結構化網格，對VGs處進行網格加密處理，第1層網格高度為0.01 mm，網格增長率為1.1，保證y+≤1.5，網格如圖3所示。

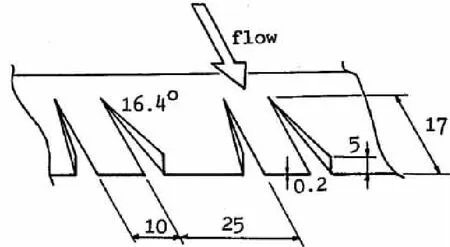
圖2 渦流發生器尺寸參數

圖3 網格劃分

1.2 數值模擬方法

3種不同弦長的翼型計算雷諾數相同，計算雷諾數為Re=2.0×106，攻角范圍為0°到20°，所采用的數值計算方法與文獻[8]相同，即使用轉捩模型進行數值模擬計算，定義三維翼型兩側的斷面為周期性邊界條件。

2 計算結果分析

2.1 模型驗證

圖4為轉捩模型計算的升力系數曲線與試驗數據的對比圖。從試驗數據可以看出，VGs使翼型失速現象明顯延遲，從無VGs翼型的臨界攻角12.37°延遲到有VGs 翼型的16.51°，將最大升力系數由1.55提升到了1.97。從計算結果可以看出，轉捩模型計算結果與試驗結果吻合良好。在攻角范圍為0°≤α≤18°時，轉捩模型計算誤差僅為5.28%，在α>18°時轉捩模型計算誤差僅為6.51%。由此可見，轉捩模型對于渦流發生器的數值計算精度高，其模擬結果能真實地反映VGs翼型的氣動特性。

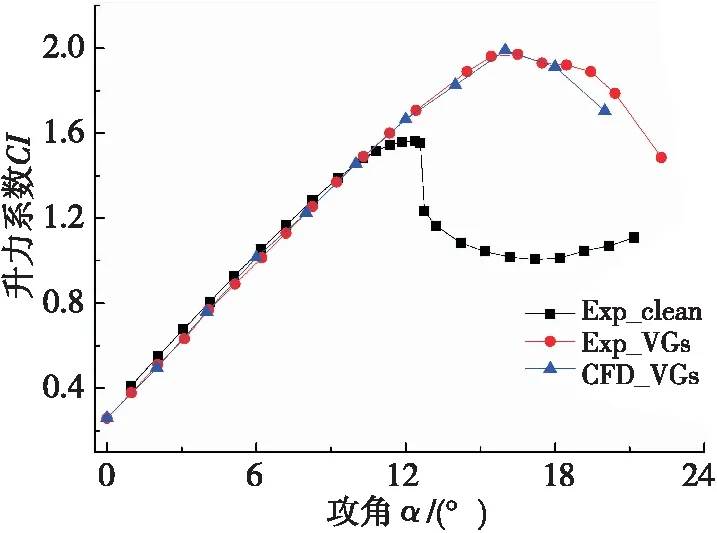
圖4 升力系數曲線

2.2 VGs對流場和表面壓力分布的影響

從升力系數的變化趨勢可以看出，α=18°位于VGs翼型的升力系數曲線的臨界攻角附近，此時翼型表面可能會出現氣流分離現象，截取如圖5所示的位置1和位置2對應的截面，截面1為每組VGs的中心線，截面2為相鄰2組VGs的中心線。

圖5 位置1和位置2

圖6為截面1和截面2的流線圖。從兩個截面的流線圖可以發現兩個截面的流場是不同的，截面1尾緣處未出現明顯分離區域，截面2尾緣處出現明顯的分離區域，這表明翼型段上VGs的下游氣流在沿展向分布上是不均勻的。

圖7為截面1和截面2與翼型交線的壓力分布圖。可以看出兩個截面的壓力分布只在安裝VGs附近是不同的，交線1上壓力分布出現負壓峰值，而交線2上出現負壓谷值。流線圖和壓力分布揭示了流動產生渦流的根本原因，對于單個渦流發生器而言，當氣流經過時，其兩側變成了壓力面和吸力面，造成兩側壓力的不平衡，形成高能量的渦流，注入到近壁低能量氣流后，增加了近壁流體的動量和能量，從而抑制邊界層的分離，推遲翼型失速。

圖6 攻角為18°下不同截面的流線圖

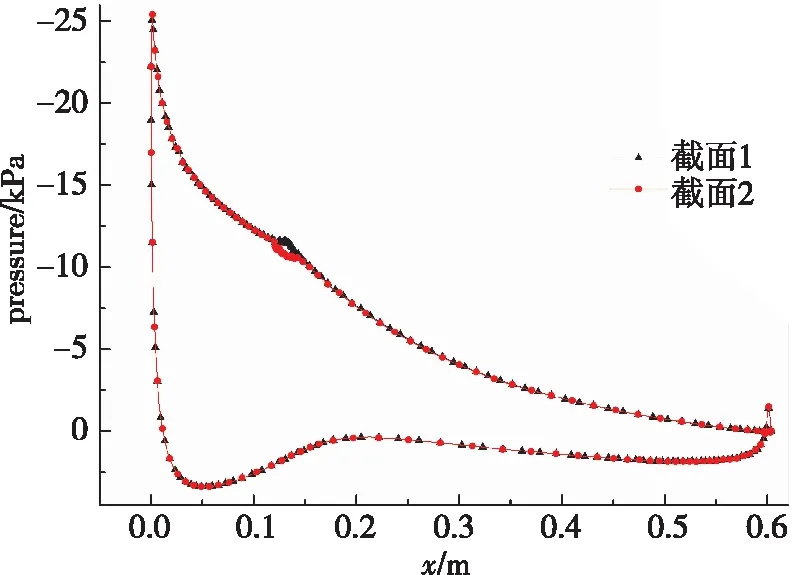
圖7 攻角為18°下不同截面壓力分布圖

2.3 翼型弦長變化對流場的影響

圖8為安裝相同VGs，翼型不同弦長的升力系數變化規律圖。可以看出，安裝了相同的渦流發生器，3種不同弦長翼型的升力系數較光滑翼型均得到了提升，對翼型弦長為0.6 m的升力系數的提升最為有效。在攻角范圍為0°≤α≤14°時，3種不同弦長翼型的升阻力系數變化趨勢基本相同，在α>14°時，相同攻角下，隨著翼型弦長增大，翼型升力系數減小。當攻角為16°時，弦長1 m的翼型升力系數較0.6 m時減小了4.35%，弦長1.5 m的翼型升力系數較0.6 m時減小了10.82%。

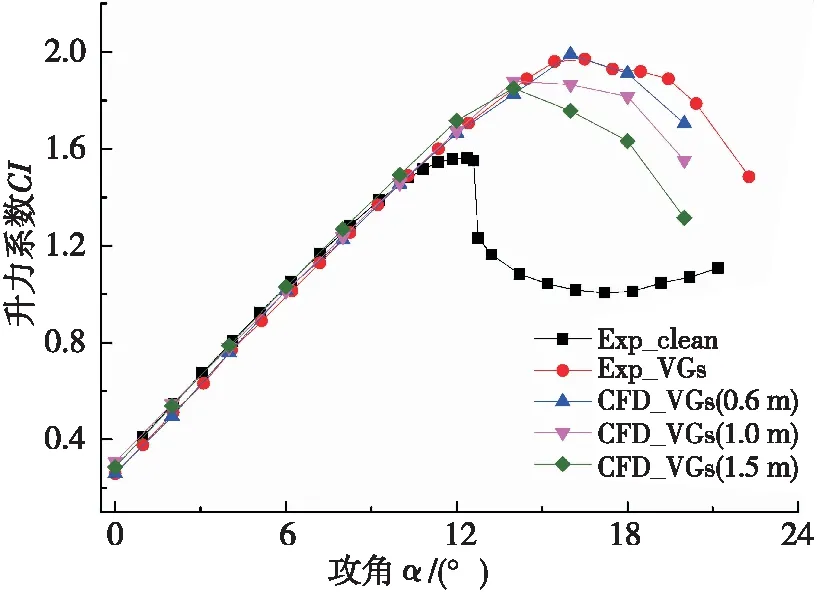
圖8 弦長對升力系數的影響

基于以上分析，截取得到3種弦長下攻角分別為14°、16°和18°時截面2的流線圖，如圖9所示。可以看出：當攻角為14°時，3種弦長的翼型尾緣處均未有明顯的分離區域；當攻角為16°和18°時，隨著翼型弦長的增大，翼型尾緣的分離區域均逐漸變大。這是因為在雷諾數相同的情況下，翼型弦長的增大意味著來流速度的減小，當流體沿著翼型表面流動并掠過VGs時，形成的渦流的動量和能量減小，與近壁低能流體混合后的流體能量將會減小， 同時混合后的流體所經過的距離增大，這就導致了翼型尾緣分離區域的增大。基于此，預測當翼型的弦長增大到4 m時，安裝本文中的渦流發生器于弦長20%處，其性能將進一步降低甚至可能失去推遲翼型失速的作用；因此，在設計適合于風場中運行的風力機葉片的渦流發生器時，應當考慮葉片截面的實際弦長。

(a)α=14°

(b) α=16°

(c) α=18°

3 結論

1) 轉捩模型計算的升力系數與試驗值吻合良好，計算精度高，可以準確地反映VGs翼型的氣動特性。VGs翼型下游流動的不均勻性形成的渦流使得近壁流體的能量增強，從而抑制邊界層的分離，推遲失速。

2)在攻角范圍為0°≤α≤14°時，3種不同弦長翼型的升阻力系數變化趨勢基本一致；在攻角大于14°時，相同攻角和雷諾數時，翼型弦長增大，升力系數減小，翼型的尾緣分離區域增大。本文的研究結果為設計適合于實際風場中的風力機葉片的渦流發生器提供了指導。