基于ADAMS的圓環鏈傳動系統仿真分析

于之龍

（山西新景礦煤業有限責任公司， 山西 陽泉 045000）

引言

圓環鏈傳動是一種嚙合傳動方式。圓環鏈傳動有很多優點，很強的適應能力、承受外力沖擊的能力和抗震能力、較高傳動效率，同時安裝水平的要求比較低[1]。由于其非常多的優點，因此被廣泛地應用在很多行業，如冶金、航天、食品加工等[2]。圓環鏈傳動也有一定缺點，圓環鏈傳動的多邊形效應致使其運動的穩定性能比較差，平穩性不夠使得傳動過程中動載荷增大，動載荷會進一步損壞傳動鏈條[3]。學者們通過廣泛的研究來尋求解決圓環鏈傳動過程中存在問題的辦法。

1 三維實體建模

三維建模的軟件和方法有很多，通過比較各個建模軟件的效率，本文選擇Pro/E建模軟件進行圓環鏈傳動裝置模型的建立。

1.1 零部件建模

圓環鏈傳動系統由很多部件組成，其中圓環鏈和鏈輪是圓環鏈傳動系統的重要組件。平鏈環和立鏈環連接起來構成了圓環鏈。通過焊接得到平鏈環，通過鍛造得到立鏈環。立鏈環和平鏈環的規格為48 mm×152 mm，根據國標《礦用圓環鏈驅動鏈輪》，建立與立鏈環和平鏈環規格匹配的鏈輪。

1.2 系統裝配

為了節約仿真模擬耗用時間，在保證仿真結果準確性的基礎上，只分別布置10個鏈環在上、下邊鏈上。

2 ADAMS中的仿真模型

將裝配好的圓環鏈傳動裝置模型接入ADAMS中，同時為了簡便處理，把模型里的零件當做不會變形的剛體來處理，所有零件屬性均定義為鋼。

2.1 定義接觸

2.1.1 鏈環與鏈輪之間的接觸

鏈環和鏈輪之間通過嚙合實現相互接觸，從而帶動整個傳動系統進行運轉，因此在建模過程中需要對鏈環與鏈輪之間的接觸進行定義。在ADAMS中存在兩種不同的計算接觸模型，分別為IMPACT函數模型和恢復系數模型，這兩種模型有各自不同的特點。前者雖然模擬仿真效果更接近實際，但是存在參數定義困難、建模時間較長的問題，后一種模型參數設置簡單，并且因其所需要的計算量比較小，仿真速度會比前一種模型快，并且效率比較高。通過對比上述兩個模型的優缺點，選擇恢復系數模型來定義鏈環與鏈輪間的接觸。

恢復系數模型參數比較少，其中關鍵的參數有恢復系數k，恢復系數表示在接觸點處碰撞后與碰撞前法向的相對速度的比值。恢復系數的大小與碰撞物體特性密切相關，碰撞物體材料和接觸面的幾何形狀影響其恢復系數的大小，恢復系數可以通過實驗獲得。恢復系數k≥0且≤1，當與碰撞物體發生的是完全非彈性碰撞時，k取0；當與碰撞物體發生的是完全彈性碰撞時，k取1。恢復系數的取值直接影響仿真的效果，當恢復系數為0時，能保證仿真高效穩定的進行，因此在接觸模型中定義恢復系數為0。

2.1.2 鏈環之間的接觸

在圓環鏈傳動系統建模仿真過程中，鏈環之間的接觸方式一般采用軸套力模型或者接觸模型來定義。但是這兩種定義接觸的方式存在很多缺點，比如：耗時過長、仿真結果精度差等。而彈簧阻尼模型能夠有效地規避接觸模型和軸套力模型的缺點，具有仿真結果精確、耗時短、穩定性好的優點，因此鏈環之間的接觸采用彈簧阻尼模型來定義。下頁圖1為彈簧阻尼模型定義的接觸。

2.2 定義約束

鏈輪的運動副為轉動副，故需要在中心處添加使其只能做旋轉運動。為了在仿真中實現對各個部件的約束，需要對定義的運動副設定一定數目的自由度，可以被定義的運動副有很多，包括齒輪副、滑移鉸鏈、耦合副等。因為鏈輪的運動副是為了讓鏈輪做旋轉運動，因此需在鏈輪上配置旋轉鉸鏈。

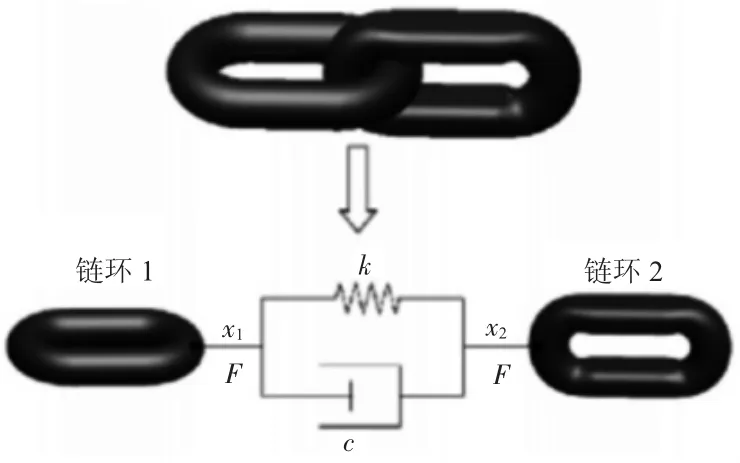
圖1 彈簧阻尼模型定義的接觸

平鏈環與鏈輪之間是線面高副嚙合，這種嚙合方式很復雜，并且平鏈環還和立鏈環一起平動，導致平鏈環運動副很難被精準定義，因此在滿足必要的仿真效果下，可不比定義平鏈環的約束，只要定義其與鏈輪之間的接觸即可，同時在鏈環上增加平動副來保證沿鏈輪中心距方向上的平動。

2.3 運行阻力

在刮板輸送機的圓環鏈傳動系統中，由于上下邊鏈的負載狀況不同，導致上下邊鏈的運行阻力不同。上邊鏈的運行阻力圓環鏈傳動系統存在上下兩個邊鏈，因兩個邊鏈負載不同，運行阻力的計算公式也不盡相同，上、下邊鏈的運行阻力[1]為：

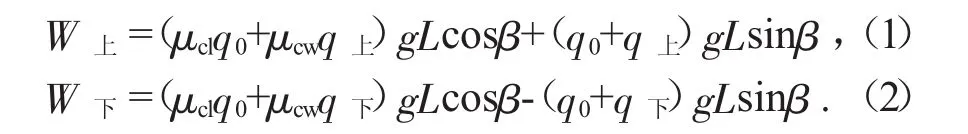
式中：μcl為中部槽與圓環鏈條之間的摩擦系數；μcw為中部槽與物料之間的摩擦系數；q0為單位長度圓環鏈條的質量；q上為單位長度上邊鏈上物料的質量；q下為單位長度下邊鏈上物料的質量；g為重力加速度；L為輸送機鏈條需要敷設的距離；β為輸送機的傾斜角度。

由公式（1）、公式（2）可知，鏈環上邊鏈和下邊鏈的阻力不同，圓環鏈所受阻力與環鏈空間位置有關，因此圓環鏈所受的阻力在建模過程中以場力來代替。

在模擬過程中用場力來代替鏈環受到的阻力，但是為了讓模擬仿真結果更加精準，還要把以下兩點考慮在內：

1）圓環鏈傳動系統在啟動的一瞬間，鏈輪只受到扭矩，又因其受到靜摩擦力的作用，鏈輪和鏈條都有運動的趨勢，但鏈輪的轉速為零。

2）為保證圓環鏈傳動系統穩定有效運行，應該避免力的陡變對傳動系統的穩定性產生沖擊，因此在鏈環與鏈輪嚙合運行的一個周期的始末，應該讓鏈輪與鏈環之間的阻力逐漸增大或者逐漸減小。

SGZ1000/2000型刮板輸送機的參數為：輸送機鏈條應敷設300 m，并且其傾斜角度在為-5°～5°之間變化；輸送機單位長度圓環鏈的質量為172.9 kg/m，輸送機上鏈上單位長度的物料質量為441.5 kg/m，輸送機下邊鏈上的物料質量忽略不計;圓環鏈與中部槽間的動摩擦系數和靜摩擦系數在0.3～0.4之間；輸送鏈上的物料與中部槽間的動摩擦系數和靜摩擦系數在0.6～0.8之間[2]。

根據上述公式，并把圓環鏈相應的參數帶入公式，可以求得輸送機上邊鏈的運行阻力為500 N，上邊鏈的靜運行阻力為600 N；下邊鏈的運行阻力為80 N，下邊鏈靜運行阻力為100 N。

3 建立電機模型

傳動系統需要電機來提供運行動力，因此需要在仿真模擬過程中添加電機模型，但是真實的電機模型比較復雜，難以在ADAMS中實現。因此在確保仿真結果真實可信的基礎上建立電機簡化模型，設定此簡化模型的啟動力矩值固定不變，當電機轉速到達臨界值時，采用階躍式函數來表征特性函數。如圖2所示。

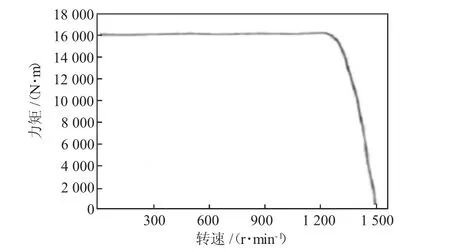
圖2 電機的簡化機械特性曲線

4 仿真結果

圓環鏈傳動系統運行一個周期得到的結果如下頁圖3和下頁圖4所示。圖3為鏈輪的轉速曲線，圖4為鏈環間作用力的變化曲線。由下頁圖3可知，0.025 s前，鏈輪轉速呈現整體減小的趨勢，在0.025 s后，因鏈環與鏈輪的周期性嚙合，鏈輪轉速曲線出現振蕩特性。由下頁圖4可知，在0.1 s前，鏈環之間的作用力整體呈現增大趨勢，在0.1 s處達到峰值，在0.1～0.2 s之間鏈環之間作用力不斷下降，在0.2 s處出現陡增，隨即在0.2～0.5 s內作用力產生振蕩，0.5 s作用力完成一個周期的變化，接下來作用力將呈現周期性變化[3]。

根據上述仿真結果可知，鏈輪轉速以及鏈輪與鏈環之間作用力在一定時間段內都呈現振蕩現象，這是由于鏈輪與鏈環在即將嚙合或者脫離嚙合時，鏈式傳動系統出現多邊形效應。模擬的結果和圓環鏈系統實際運行結果相符，有效地驗證了這種建模方式的合理性。

圖3 鏈輪轉速

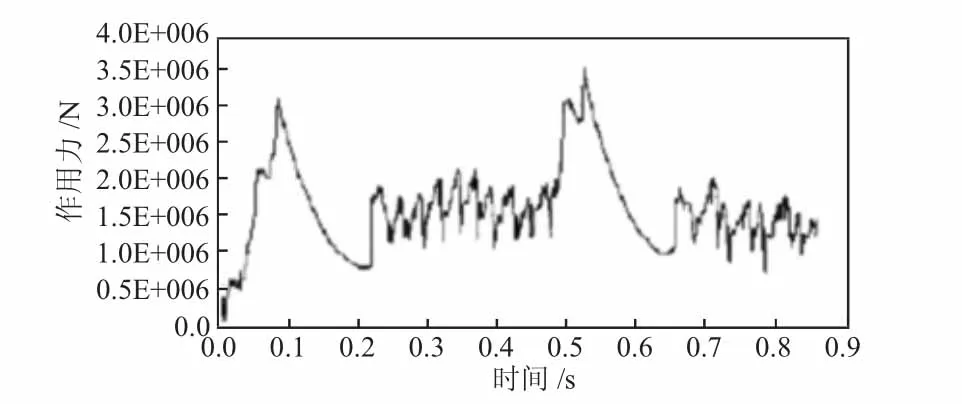
圖4 鏈環間作用力

5 結論

結合三維實體造型軟件和動力學分析軟件，構建以圓環鏈傳動系統為原型的虛擬樣機模型。在仿真模擬過程中，用彈簧阻尼模型來定義鏈環之間的接觸，確保最終模擬結果的準確性，并且用彈簧阻尼模型來定義接觸會縮短模型計算所耗用的時間。鏈環受到的阻力在模擬過程中用場力來代替，既能保證模擬仿真結果的真實性，又能保證其準確性。最終模擬仿真得到的結果與圓環鏈傳動系統真實的模擬結果一致，有效驗證了基于動力學分析軟件ADAMS得到的圓環鏈傳動系統模型的有效性。