有外部擾動的隨機純反饋非線性系統的自適應模糊控制

,

(山東科技大學 數學與系統科學學院, 山東 青島 266590)

近年來, 非線性系統的控制問題廣泛存在于物理設備的研究中, 如生物光學、機械執行器等, 因此對于非線性系統的控制方案已有很多研究成果[1-4]。 特別的, 一些以線性逼近為基礎的自適應控制方案已經從確定非線性系統[5-7]擴展到隨機非線性系統[8-11]。 文獻[8]研究了具有未知時間延遲的單輸入單輸出嚴格反饋非線性隨機系統, 提出了一種自適應模糊控制方案。文獻[9]針對一類不確定隨機非線性嚴格反饋系統提出了兩種自適應模糊輸出反饋控制方法。 文獻[10]設計了一個模糊狀態觀測器來估計未測量的狀態, 研究一類具有不可估量狀態的不確定隨機純反饋非線性系統的自適應模糊輸出反饋問題。 此外, 通過結合模糊邏輯系統的逼近能力和反推技術,非線性系統已經成為研究模糊控制問題的重要工具。 文獻[11]考察了非嚴格反饋形式的單輸入單輸出非線性隨機系統的自適應模糊控制問題, 其中用模糊邏輯系統來逼近不確定非線性函數, 并采用反推技術構建了自適應模糊控制器。 文獻[12]針對一類具有非嚴格反饋形式和未知非線性死區的非線性系統的自適應模糊跟蹤控制問題, 基于模糊邏輯系統的逼近能力和反推技術, 提出了自適應模糊控制方案。 然而, 上述結果中的未知函數都是仿射形式的, 即輸出的狀態方程是線性形式。

純反饋非線性系統中的未知函數是無仿射形式。 對于純反饋非線性系統, 基于中值定理,先后提出了一些自適應模糊控制方案[13-15]。 文獻[13]針對一類具有時變延遲的不確定隨機純反饋系統, 提出了自適應神經控制方案。 文獻[14]提出了一類具有未知滯后的隨機純反饋非線性系統的自適應模糊控制方案。 文獻[15]對于隨機純反饋非線性系統, 提出了一類自適應神經網絡控制方案。 然而, 這些研究忽略了外部擾動的影響。 在實踐中, 外部擾動時常是系統不穩定的來源, 帶有外部擾動的系統對于自適應率和虛擬控制信號的設計有著更高的要求, 帶有外部擾動的系統比一般系統的研究更加困難。 近年來, 對于帶有外部擾動的系統研究有了一些結果[16-19]。 而對于帶有外部擾動的隨機純反饋非線性系統的研究成果較少。

不同于文獻[20]研究的是確定系統, 也不同于文獻[21]中忽略了外部擾動，本文研究的是有外部擾動的隨機純反饋非線性系統的自適應模糊控制問題。 利用中值定理, 結合反推方法, 提出了一種新的自適應模糊控制方案。

1 準備工作和問題陳述

先介紹以下隨機非線性系統:

dx=f(x,t)dt+h(x,t)dw,

(1)

其中,x∈Rn是狀態變量,f:Rn×R+→Rn,h:Rn×R+→Rn×r是連續函數。w是定義在完備概率空間(Ω,F,{Ft}t≥0,P)上的r維獨立標準布朗運動, 其中Ω是樣本空間,F表示σ域, {Ft}t≥0表示范圍,P是概率測度。

定義1[22]對于二次連續可微函數V(x,t), 定義一個微分運算符L, 則:

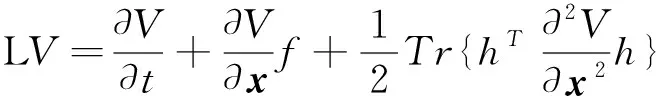
(2)

其中,Tr是矩陣的跡。

考慮以下帶有外部擾動的隨機非線性系統:

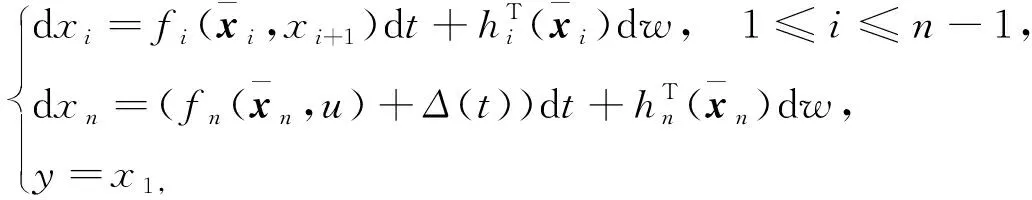
(3)

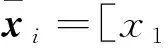
對于系統(3), 定義:

(4)

其中xn+1=u。

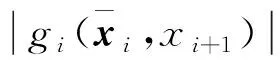
(5)

使用模糊邏輯控制系統來逼近定義在完備集Ω上的一個連續函數f(x)。 采用單點模糊化和中心平均模糊化推論得到以下模糊規則[14]:

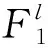
thenyisGl,l=1,2,…,N。

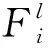
(6)

其中

令

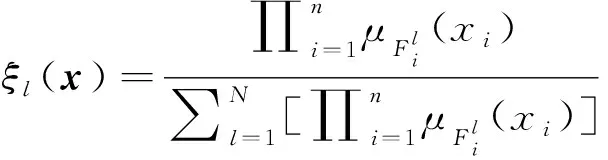
模糊邏輯系統(6)可以重新寫為

y(x)=φTξ(x)。

(7)

引理1[14]設f(x)是定義在完備集Ω上的連續函數。 對?ε>0, 存在一個模糊邏輯系統(7), 使得

(8)

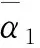
則存在系統(1)的一個特解, 對每一個x0∈Rn, 滿足:

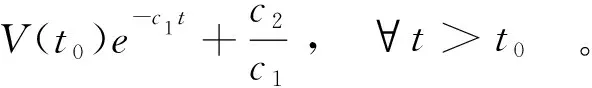
(9)

并且V(x,t)是有界的。

引理3[24]對?(x,y)∈R2, 以下不等式成立:

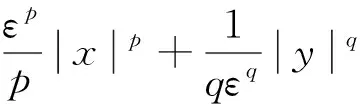
其中ε>0,p>1,q>1,(p-1)(q-1)=1。

引理4[24]考慮以下動態形式:

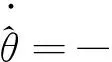
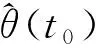
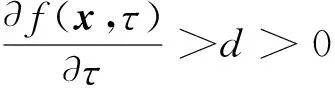
f(x,τ*)=0。

(10)

控制目標是: 設計一個自適應模糊控制方案, 使得系統輸出y跟蹤到參考信號yd, 并且閉環系統的所有信號是有界的。

假設2參考信號yd(t)以及它的n階導數, 都是連續有界的。

2 設計自適應控制器

現在利用反推方法, 設計非線性系統(3)的自適應控制方案。 定義以下坐標變換:

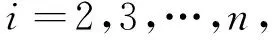
(11)

其中αi-1是一個中間控制函數。

第1步考慮系統(3), 由z1=y-yd, 知動態誤差滿足

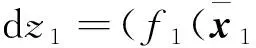
(12)

選擇以下Lyapunov函數

(13)

其中r1是正常數。 由式(2)和式(11)、(12), 知

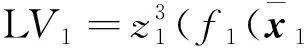
(14)

根據引理3, 以下不等式成立

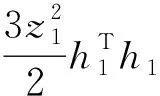
(15)

其中l1是正常數。 將(15)代入(14)式, 有

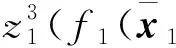
(16)

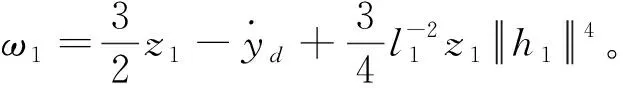
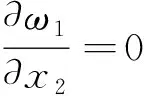
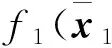
(17)

根據中值定理, 存在μ1(0<μ1<1), 使得

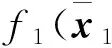
(18)

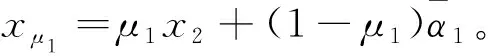
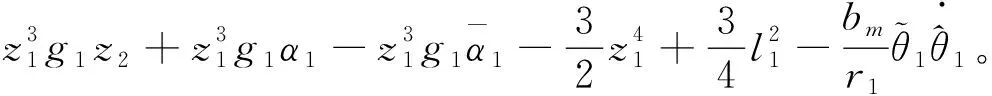
(19)

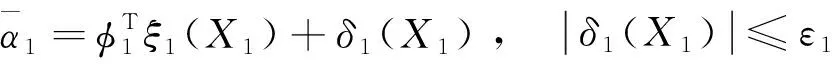
(20)

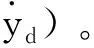
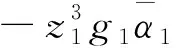
(21)

其中a1是正常數。 選擇虛擬控制信號和自適應率分別為

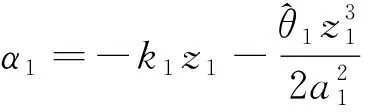
(22)

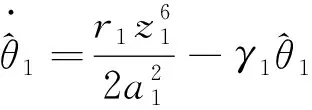
(23)

其中k1和γ1是正常數。 由(25)和假設1知

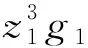
(24)

再由引理2及假設1, 得

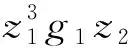
(25)

把式(21)～(25)代入式(19), 得

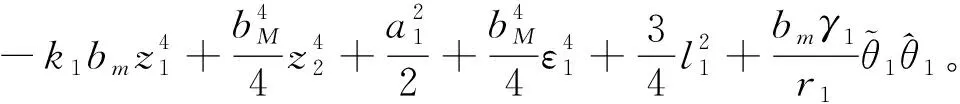
(26)

又

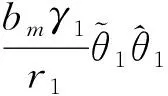
(27)

所以式(26)可以化為

(28)

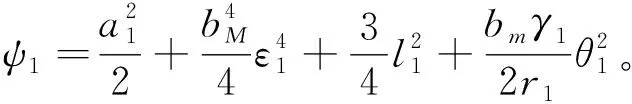
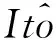
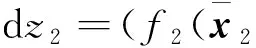
(29)

其中

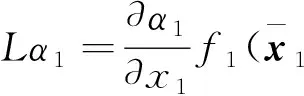
(30)

選擇以下Lyapunov函數

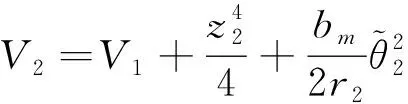
(31)

其中r2是正常數。 由式(2)和式(29), 有

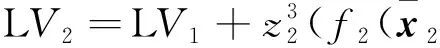
(32)

由引理3, 得

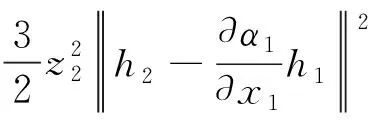
(33)

其中l2是正常數。 將式(28)、(33)代入式(32), 有

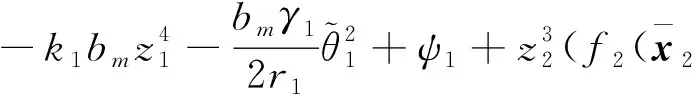
(34)

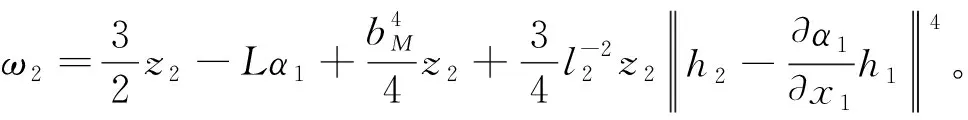
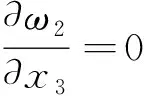
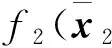
(35)

根據中值定理, 存在μ2(0<μ2<1), 使得

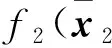
(36)

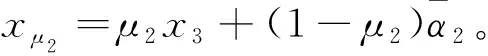
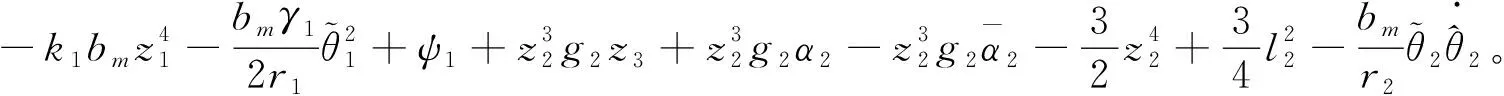
(37)

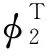
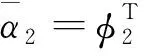
(38)

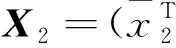
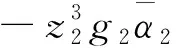
(39)

其中a2是正常數。 選擇虛擬控制信號和自適應率分別為

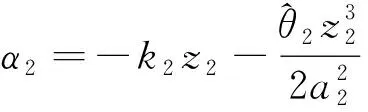
(40)

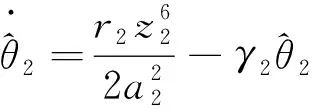
(41)

其中k2和γ2是正常數。 由式(40)和假設1知

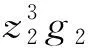
(42)

再由引理2及假設1, 得

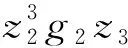
(43)

注意到

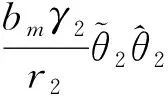
(44)

把式(39)～(44)代入式(37), 得

(45)

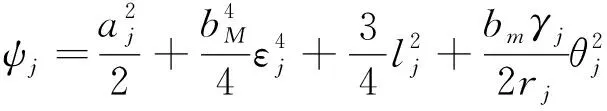
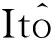
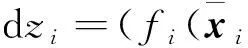
(46)

其中

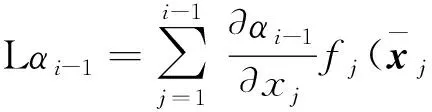
(47)

選擇以下Lyapunov函數：

(48)

其中ri是正常數。 由(2)和(46), 有

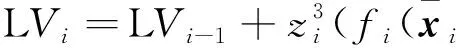
(49)

由引理3, 得

(50)

其中li是正常數。 將(50)代入(49)式, 有

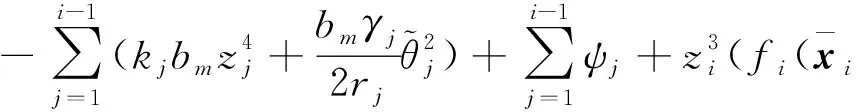
(51)

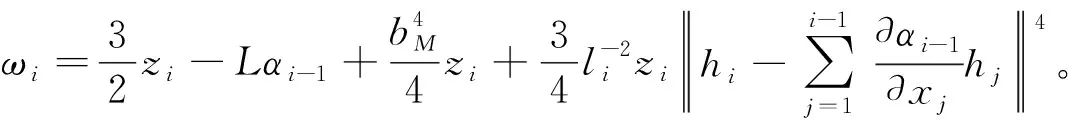
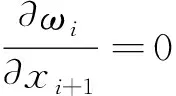
(52)

根據中值定理, 存在μi(0<μi<1), 使得

(53)

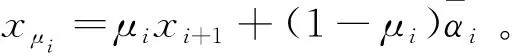
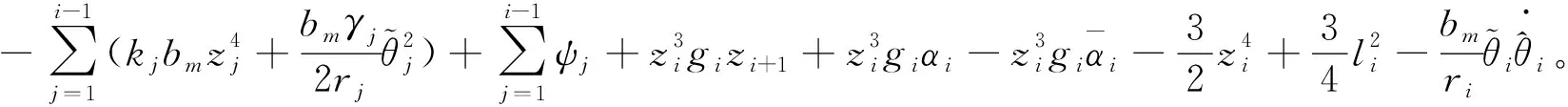
(54)

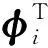
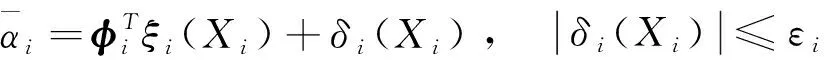
(55)

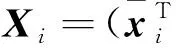
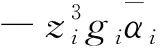
(56)

其中ai是正常數。 選擇虛擬控制信號和自適應率分別為

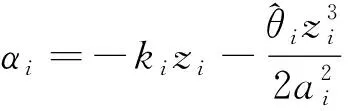
(57)

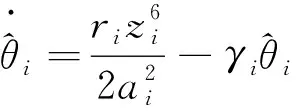
(58)

其中ki和γi是正常數。 由(57)和假設1知

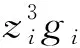
(59)

再由引理2及假設1, 得

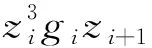
(60)

注意到

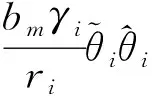
(61)

把式(56)～(61)代入式(54), 得

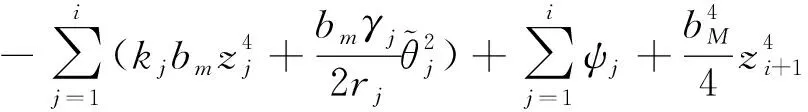
(62)

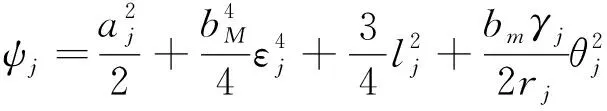
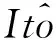
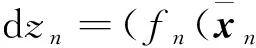
(63)

其中Lαn-1是(47)式取i=n。 選擇以下Lyapunov函數

(64)

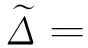
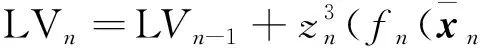
(65)

由引理3, 得

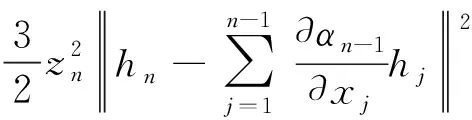
(66)

其中ln是正常數。 將(66)代入(65)式, 有

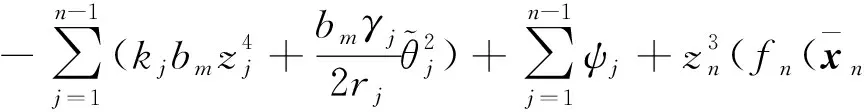
(67)

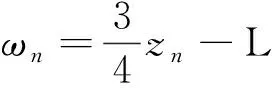
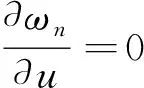
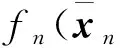
(68)

根據中值定理, 存在μn(0<μn<1), 使得

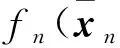
(69)

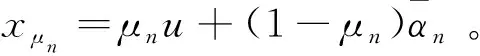
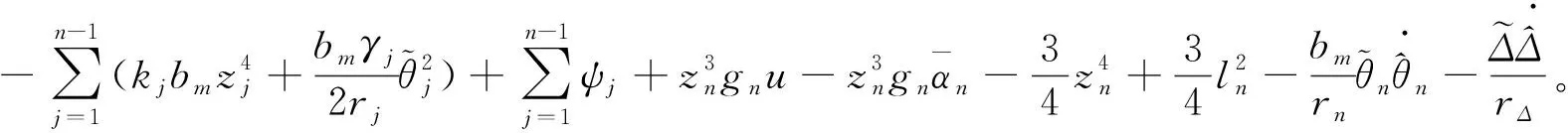
(70)

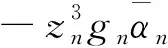
(71)

其中an是正常數。 選擇虛擬控制信號和自適應率分別為

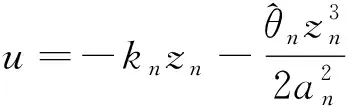
(72)

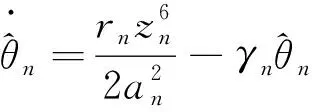
(73)

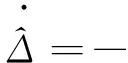
(74)

其中kn、γn和σΔ是正常數。 把式(71)～(74)代入式(70), 得

(75)

又

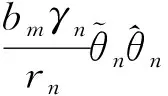
式(75)可以重新寫為

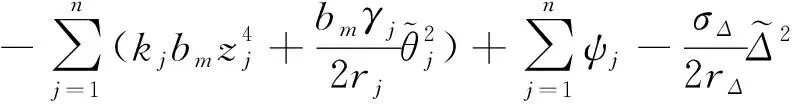
(76)

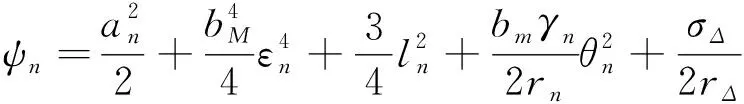
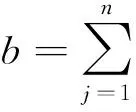
(77)

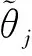
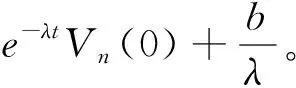
(78)

故

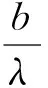
(79)

從而

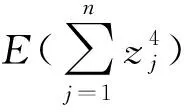
(80)

因此,zj收斂到完備集ΩZ, 其中

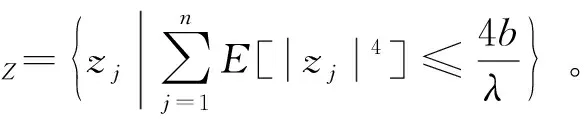
(81)

基于反推技術, 自適應模糊控制器設計完成, 有如下結論。

定理1在假設1和2及初始條件下, 對于隨機純反饋非線性系統(3), 通過設計虛擬控制信號(57)和(72), 以及自適應率(58)和(73)～(74), 保證了閉環系統的所有信號一致有界, 并且跟蹤誤差收斂到原點的小領域。

3 仿真算例

為了說明所提出方案的有效性, 考慮以下二階隨機純反饋非線性系統:

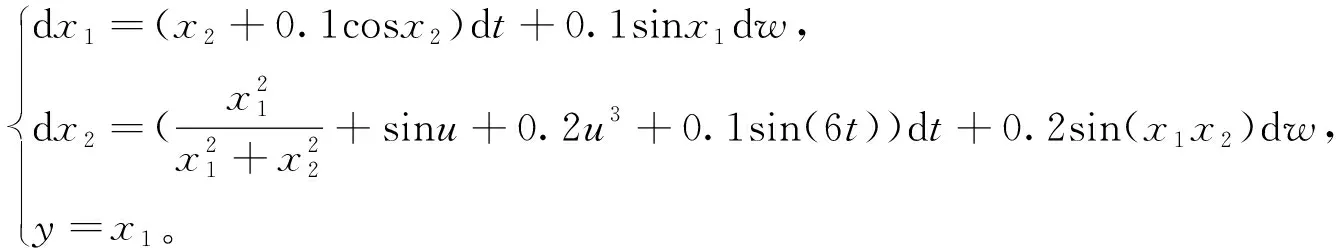
(82)

控制目標是設計一個自適應模糊控制器, 使得閉環系統的所有信號是有界的, 并且系統輸出y跟蹤到參考信號yd=0.5cost+sin(0.5t)。 根據定理1, 選擇以下的虛擬控制信號和自適應率:

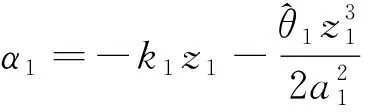
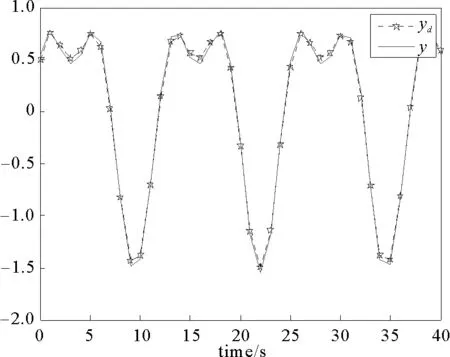
圖1 系統輸出y和參考信號ydFig.1 System output yand reference signalyd

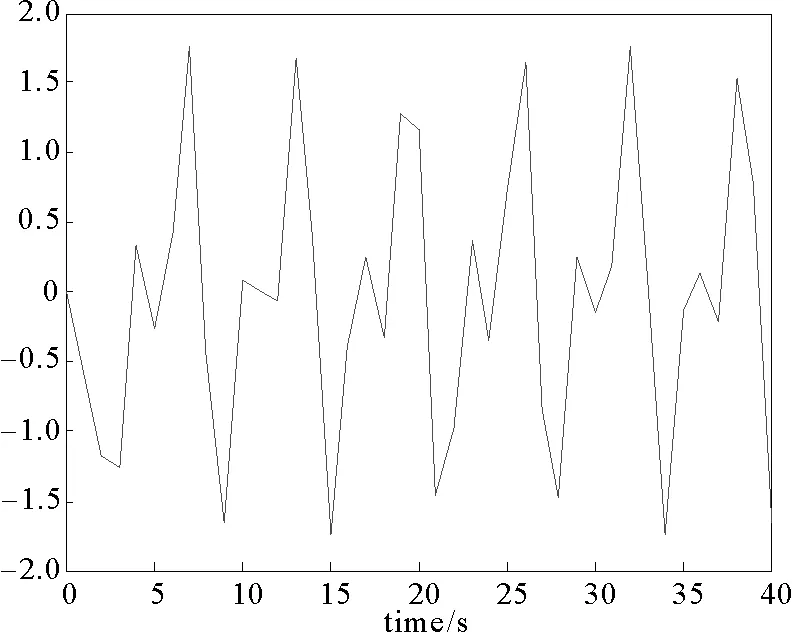
圖2 狀態變量x2Fig.2 State variable x2

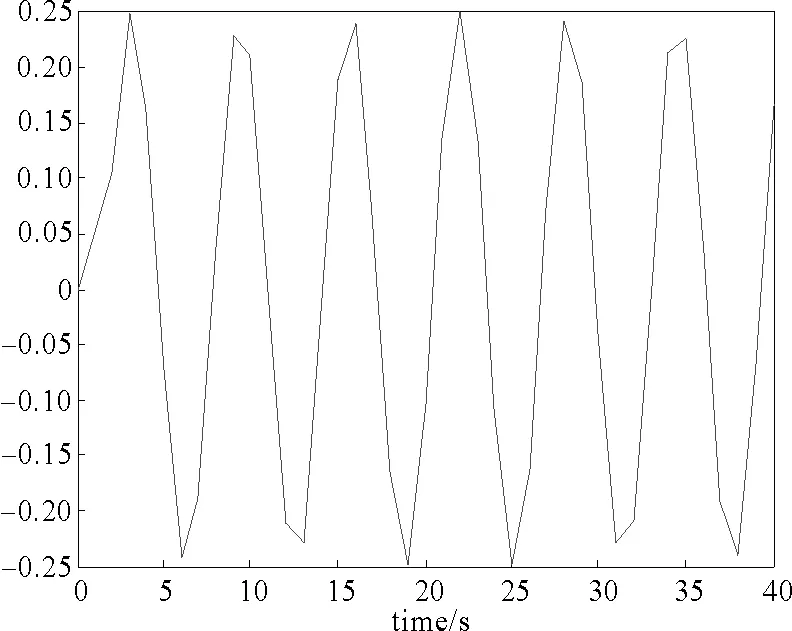
圖3 系統輸入uFig.3 System output u

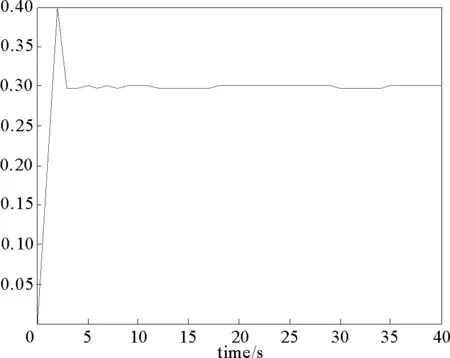
圖4 有界外部擾動的估計

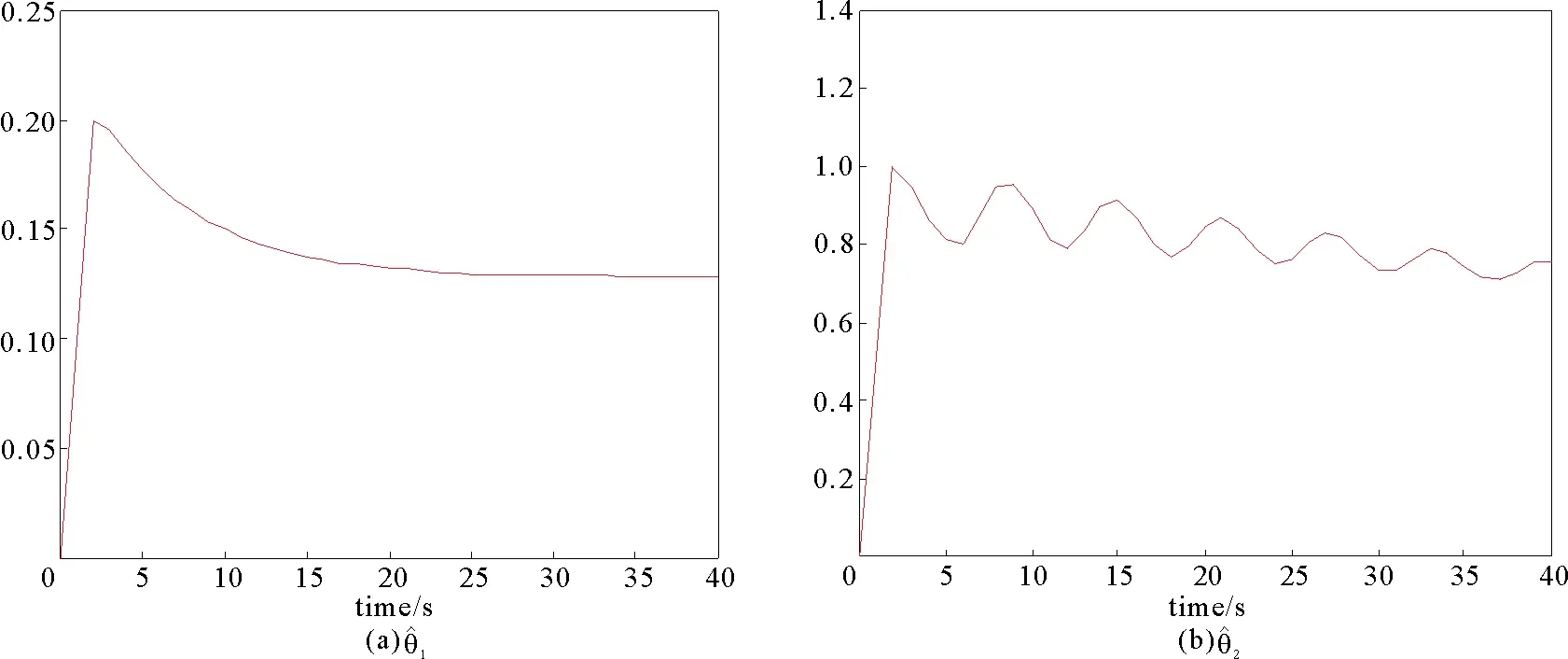
圖5 自適應率和Fig.

仿真結果表明了所提出方案的有效性, 保證了系統輸出跟蹤到參考信號, 并且閉環系統的所有信號是有界的。

4 總結

針對一類具有外部擾動的隨機純反饋非線性系統的跟蹤控制問題, 利用中值定理結合反推技術, 設計了一個新的自適應模糊控制方案。 該控制方案保證了閉環系統的所有信號是有界的, 并且跟蹤誤差收斂到原點的小領域。