SOBOLEV INEQUALITIES FOR MOEBIUS MEASURES ON THE UNIT CIRCLE
LEI Liang-zhen,MA Yu-tao,XUE Dan-dan
(1.School of Mathematical Sciences,Capital Normal Univeristy,Beijing 100048,China)
(2.School of Mathematical Sciences,Beijing Normal University,Beijing 100875,China)
(3.The High School Affiliated to Minzu University of China,Beijing 100081,China)
Abstract:In this paper,we consider Moebius probability on the unit circle.By using the method in[1]and[2],we transfer the estimates on Moebius probability onto one-dimensional diffusion,and obtain two-sided estimates on optimal Poincaré constant,logarithmic Sobolev constant and Sobolev constant for Moebius measures on the unit circle.
Keywords:Moebius measures;Sobolev inequalities;Poincaré inequalities;logarithmic Sobolev inequalities
1 Introduction
Let n ≥ 2 and let Sn?1be the unit sphere on Rnequipped with geodesic distance d and the uniform probability measureμ.For x∈ Rnwith|x|< 1,we consider the probability measure on Sn?1given by
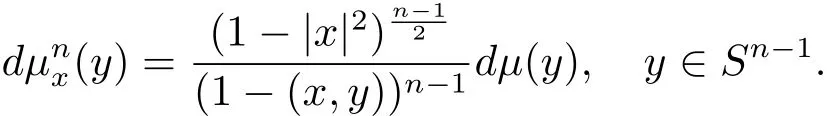
It is the so-called Moebius measure we are working on.In fact,this probability is the image ofμ under the Moebius transformation.The factoris known as the invariant Poisson kernel P(x,y):as a function of x,it is not harmonic but satisfies the equationP(·,y)=0,wheredenotes the invariant Laplacian operator(the reader is referred to[3]for further information on this measure).
Let M be a connected complete Riemannian manifold with Riemannian metric d and?is the gradient on M.Let M1(M)be the space of all probabilities on M.Given anyμ∈M1(M),we say that
1. μ satisfies a Poincaré inequality with a non-negative constant C if for any smooth function f:M→R,there exists a constant C≥0 such that

The optimal constant above is denoted by CP(μ).
2.μsatisfies a logarithmic Sobolev inequality with a constant C≥0 if for any smooth function f:M →R withμ(f2)=1,
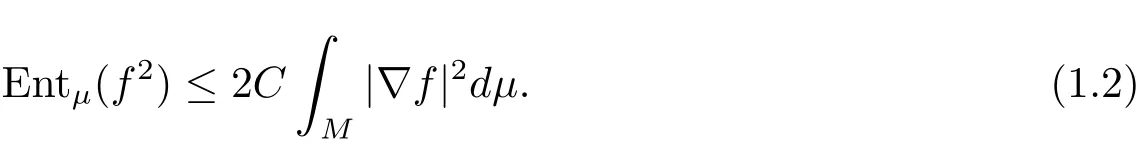
We denote by CLS(μ)the optimal logarithmic Sobolev constant.
3.μsatisfies a Sobolev inequality with exponent p≥1,if there exists one positive constant C such that for any f:M→R smooth enough,
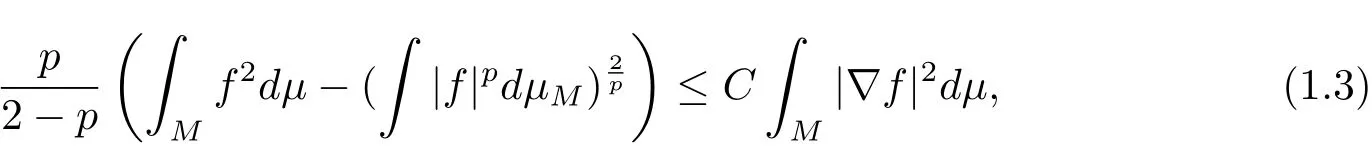
In fact,the classical Poincaré inequality corresponds to the case p=1 and the logarithmic Sobolev inequality turns out to the limit case when p tends to 2 since
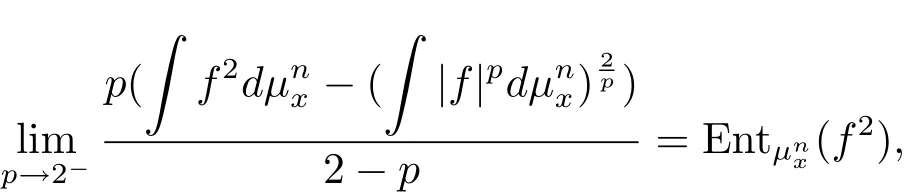
where

is the relative entropy of f2under.It was proved in[4]that
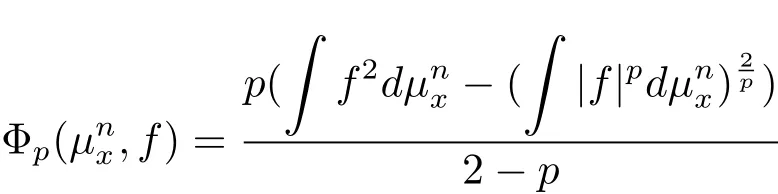
is increasing on p for given f.
In this paper,we consider the Poincaré inequality,logarithmic Sobolev inequality and Sobolev inequality for Moebius measures on the unit circle.
In[3],Schechtman and Schmuckenschl?ager proved thatwith any|x| < 1 has a uniform Gaussian concentration property,which is similar to the one of.In[5],they obtained logarithmic Sobolev and Poincaré inequalities for harmonic measures on unit sphere Sn?1for n ≥ 3 and in[2]they had similar results for harmonic measures when n=2.And then in[1],they obtained Sobolev inequalities for harmonic measures when n≥2.
Following the idea in[5],they obtained in[6]similar results for Moebius measures on unit sphere for n≥3.In this paper,we will work on the Moebius measures on unit circle
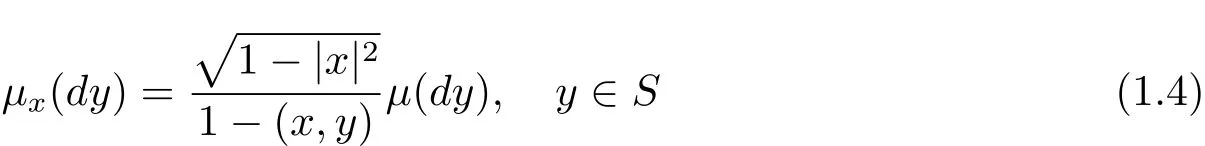
with x∈R2,|x|<1 andμthe uniform probability on the unit circle.
The main result of this paper is the following.
Theorem 1 Letμxbe the Moebius measure on the unit circle.We have
a)the optimal Poincaré constant CP(μx)satisfies
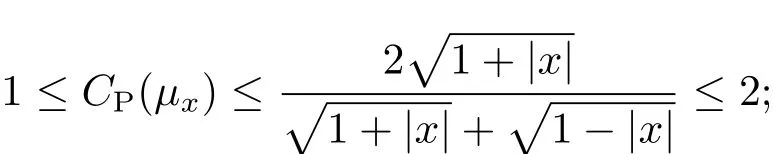
b)the optimal logarithmic Sobolev constant CLS(μx)satisfies
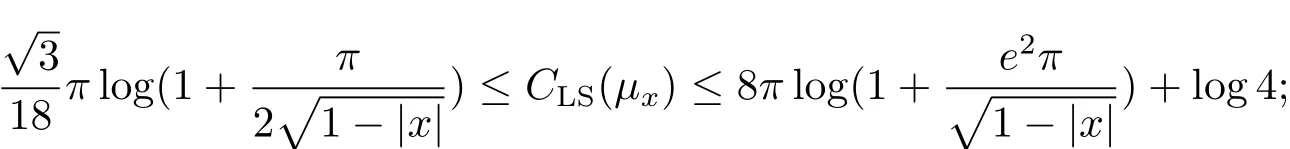
c)the optimal Sobolev constant Cp(μx)satisfies
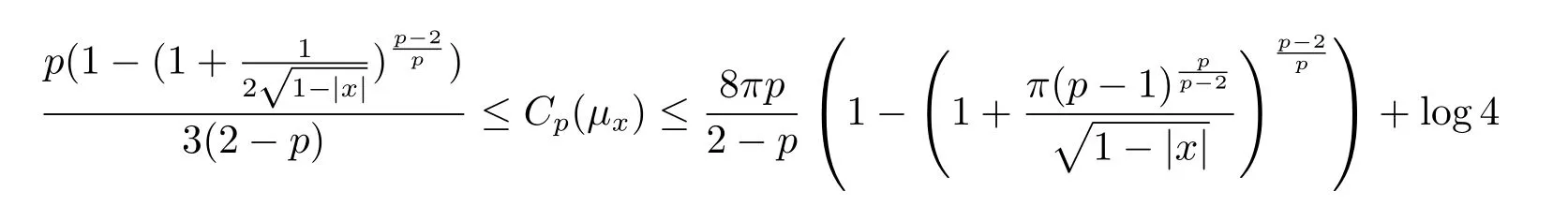
for 1<p<2.
2 Proof of the Estimate on CP(μx)
We first present a crucial lemma,which combines a particular case of Lemma 1.1 in[2]and a lemma in[1].
Lemma 2.1 Define
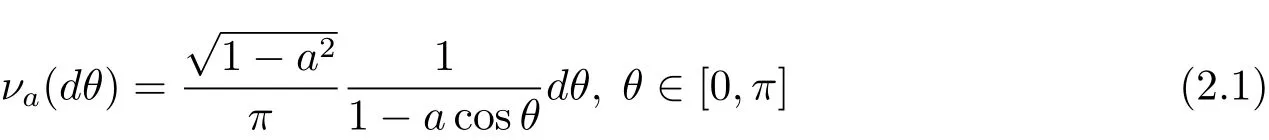
for 0<a<1.We have,respectively,
(1)the corresponding Poincaré constant satisfies
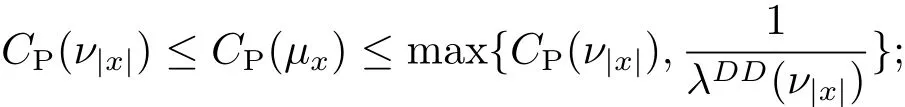
(2)similarly,the optimal logarithmic Sobolev constants satisfy
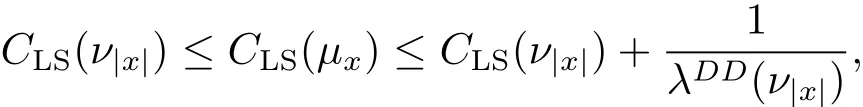
here λDD(ν|x|)is defined as

(3)the optimal Sobolev constant satisfies
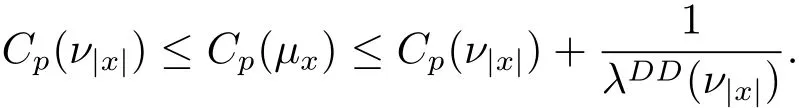
Define the diffusion operator Laas
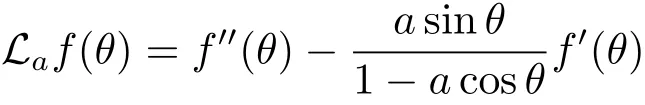
for any smooth function f:[0,π]→ R.The corresponding Dirichlet form is
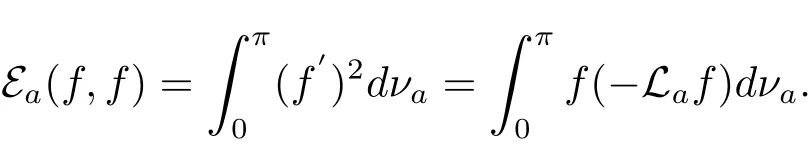
The optimal Poincaré constant,where λ1(νa)has classic variational formula
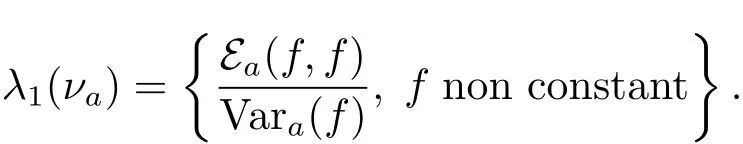
Put f(θ)=1 ? acosθ.We get
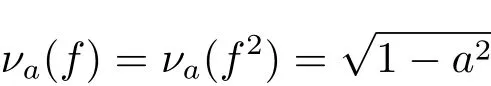
and
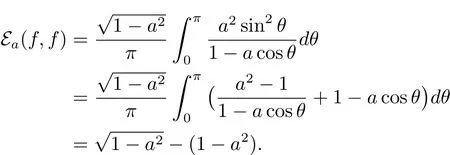
So by the variational formula
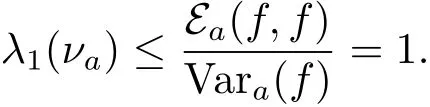
Therefore we have CP(νa)≥ 1.Now we work on the upper bound for CP(νa).The variational formula for λ1(νa)by Chen in[7]could be understood as
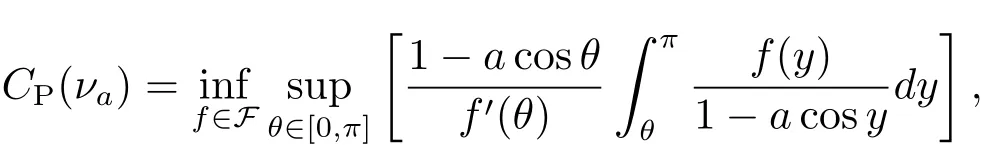
where
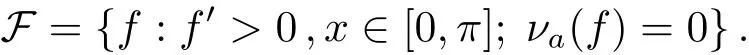
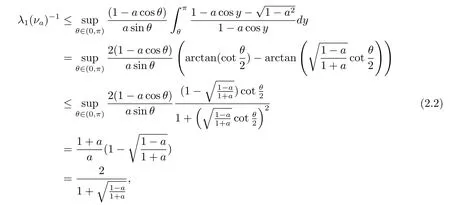
where the first equality comes true by the fact that for α ∈ [0,π],
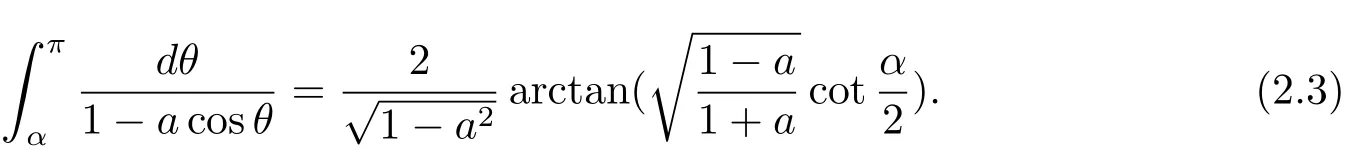
And the last but second equality holds by the fact
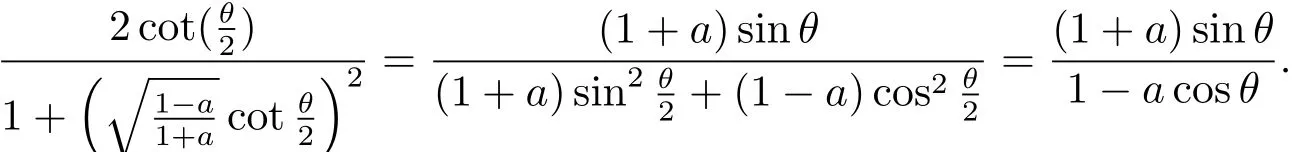
Step 1 Lower bound for λDD(νa).Choose f as f(θ)=sin θ for θ∈ [0,π].Clearly,f satisfies
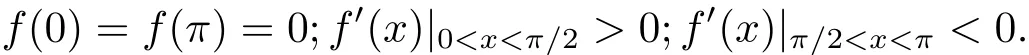
So by Theorem 1.1 in[8],

In fact,for 0≤a≤1,
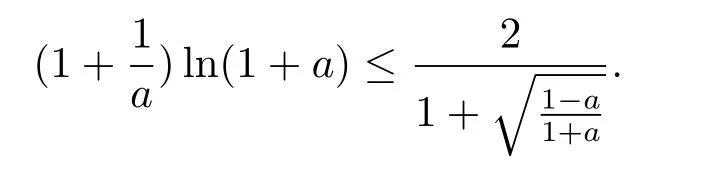
Now,combining the upper and lower bound for λ1(νa)as well as the lower bound for λDD(νa),we have by Lemma 2.1,
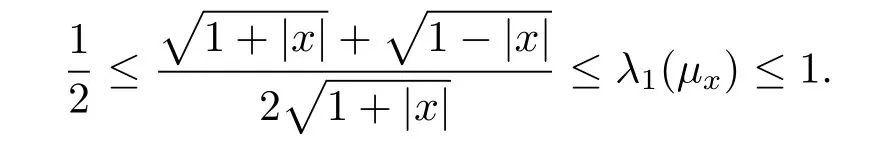
The part a)of Theorem 1 follows.
3 Proof of Log-Sobolev Inequality
By(2.3),it is clear that the median of νais θa=arccosa.Define
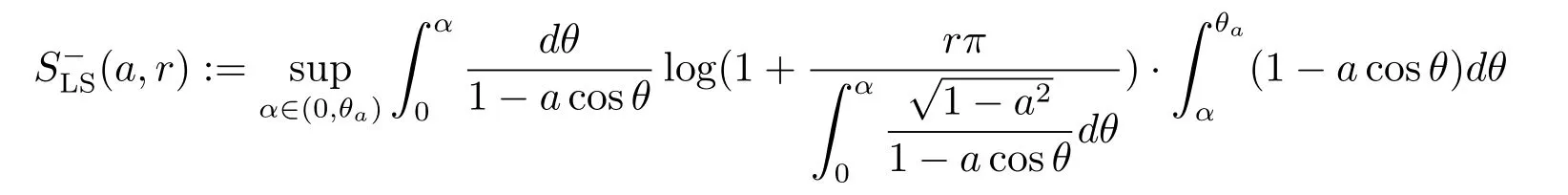
and
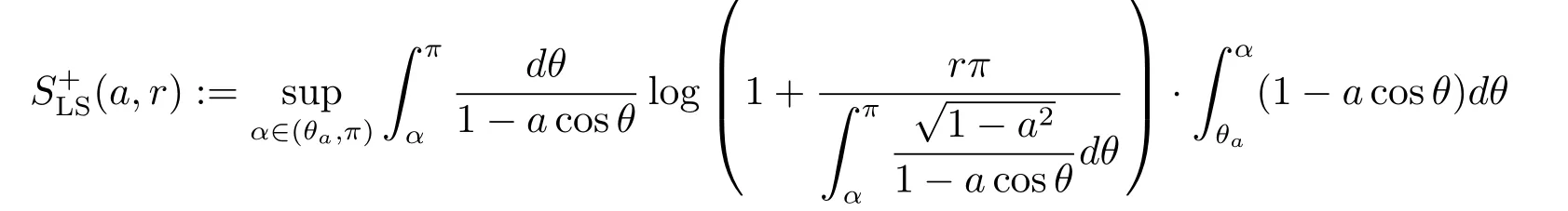
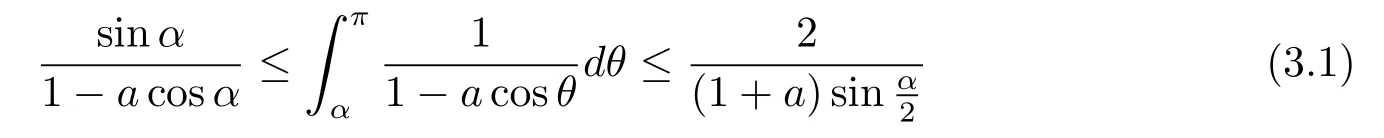
and
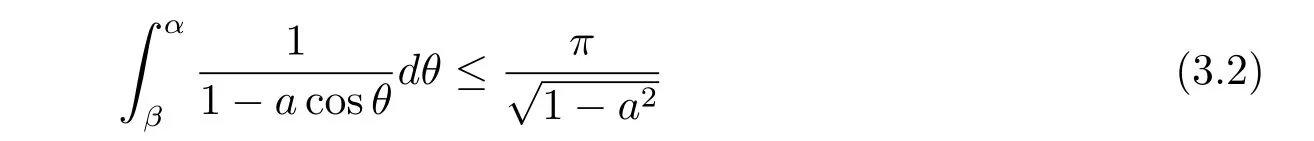
for any 0<β<α<π.

where the last inequality is true sincefor any
Similarly,by(3.2)and the fact sinwe have

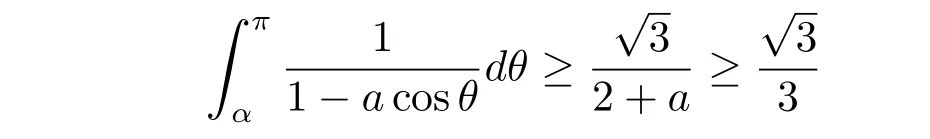
and

Therefore from the monotonicity of xlog(1+b/x)for x>0 when b>0,it holds
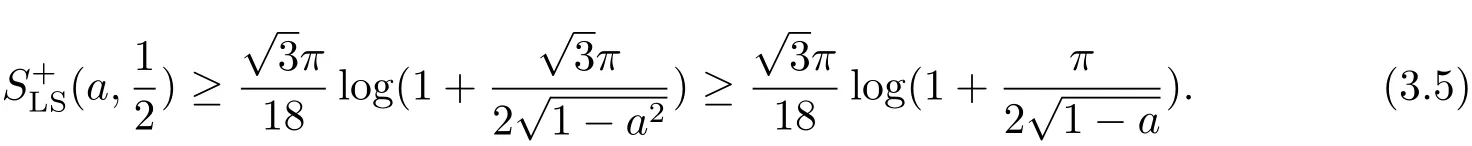
Barthe-Roberto’s characterization for logarithmic Sobolev constants tells(see[9])

Therefore,it follows from(3.3),(3.4)and(3.5)that
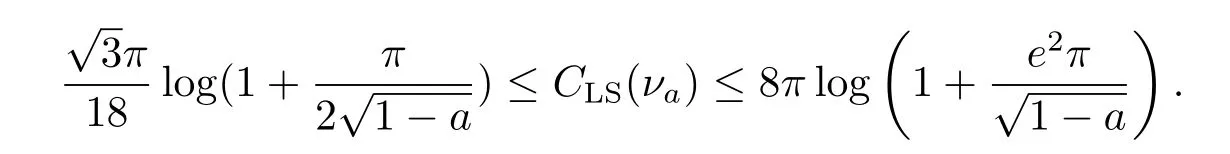
By(2.4),we have
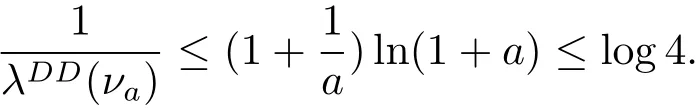
Thereby by Lemma 2.1,we get
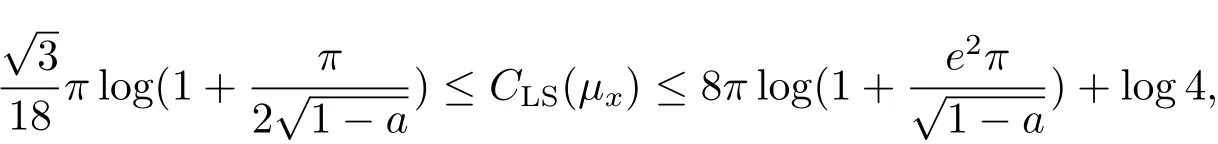
which completes the proof of b)of Theorem 1.
4 Proof of the Estimate on Cp(μx).
Define
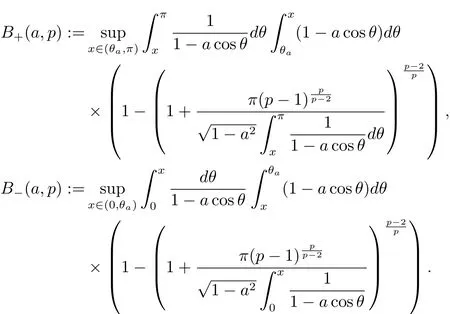
It is easy to check that bothandare increasing on R+for C>0.Recalling the estimates
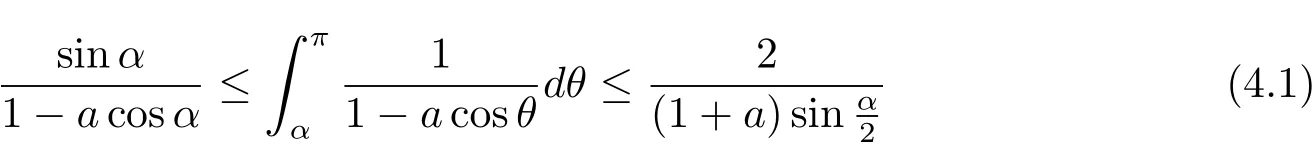
and
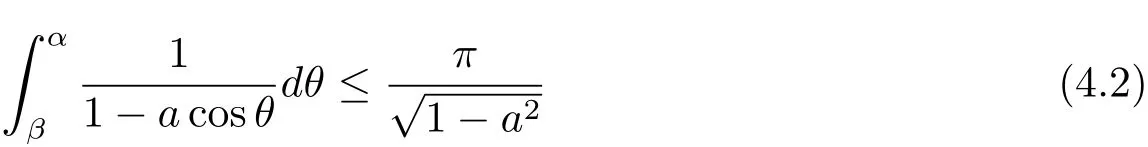
for any 0<β<α<π.We get

where the second inequality holds by
Similarly,we get
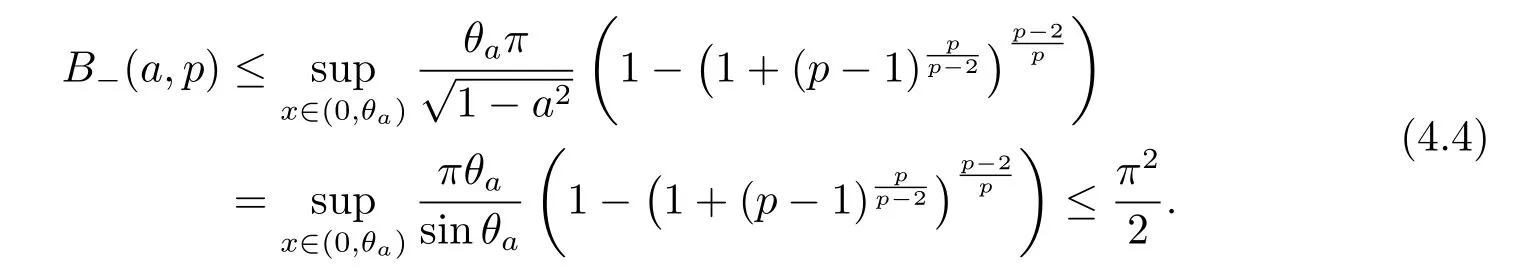
Finally,Barthe-Roberto’s characterization for Sobolev constant guarantees that
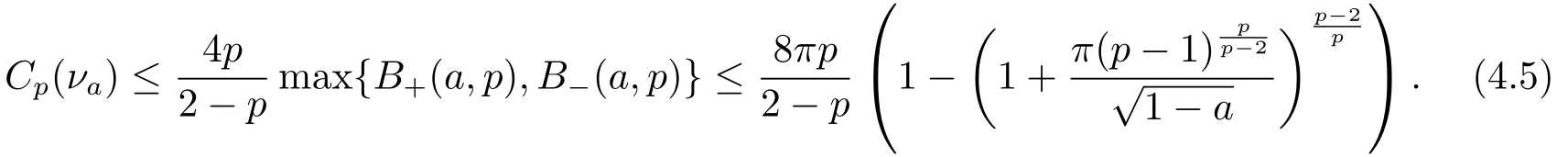
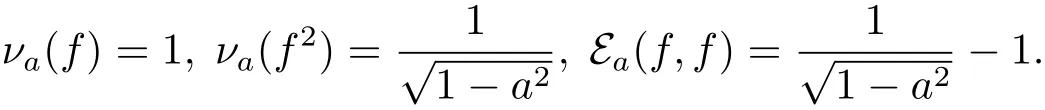
By Lemma 2.4 in[1],we know
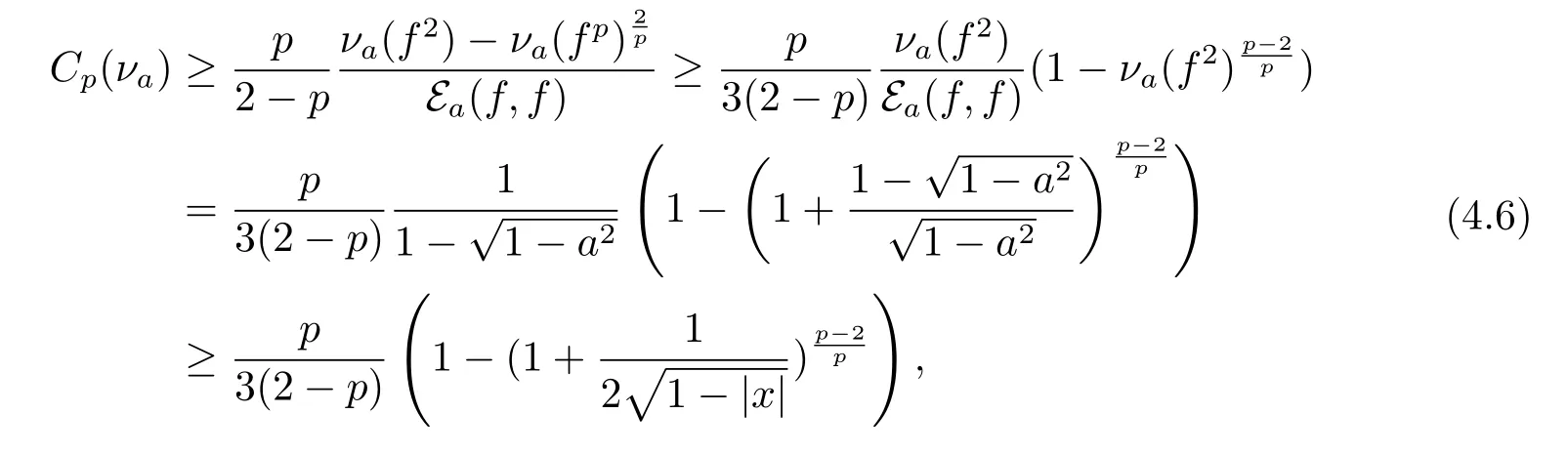
where the last inequality holds by the facts thatis increasing and1.Combining(4.5),(4.6),≤ log4 and Lemma 2.1 together,we have
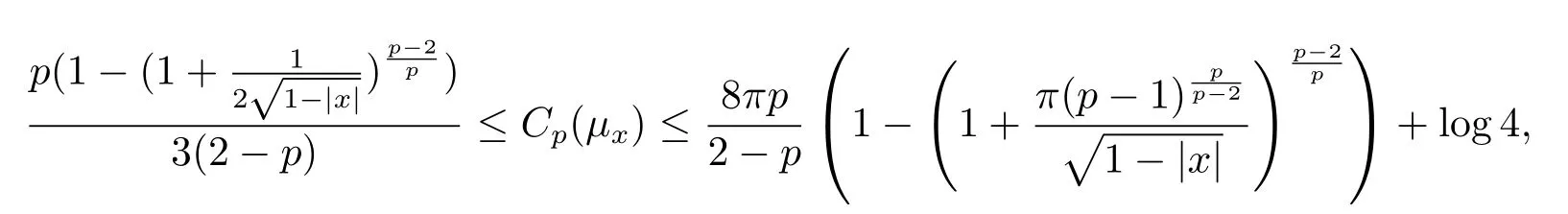
which completes the proof of theorem.

