非線性隨機(jī)參數(shù)對(duì)雙漸開線齒輪的影響分析

□ 方志遠(yuǎn) □ 張秀文

青島科技大學(xué)機(jī)電工程學(xué)院 山東青島 266061

1 研究背景

齒輪傳動(dòng)廣泛應(yīng)用于機(jī)械、汽車、航空航天及機(jī)器人等領(lǐng)域中，是一個(gè)復(fù)雜的非線性系統(tǒng)［1-2］。由于齒輪時(shí)變嚙合剛度和傳動(dòng)中間隙的存在及其它因素，會(huì)導(dǎo)致齒輪系統(tǒng)產(chǎn)生復(fù)雜的動(dòng)力學(xué)行為，其中包括準(zhǔn)周期振動(dòng)、混沌振動(dòng)等［3-4］，這些振動(dòng)往往伴隨無(wú)規(guī)律的隨機(jī)振動(dòng)。在齒輪加工過程中，由于環(huán)境、人為因素，每個(gè)齒輪的結(jié)構(gòu)尺寸并不完全相同，從而導(dǎo)致在實(shí)際傳動(dòng)過程中對(duì)運(yùn)行結(jié)果產(chǎn)生影響［5］。因此，對(duì)于隨機(jī)參數(shù)對(duì)齒輪影響的研究是非常有必要的。

在很長(zhǎng)一段時(shí)間內(nèi)，國(guó)內(nèi)外學(xué)者對(duì)隨機(jī)非線性系統(tǒng)進(jìn)行了很多理論分析和試驗(yàn)研究。WANG等［6］對(duì)非白噪聲誤差激勵(lì)下的齒輪傳動(dòng)系統(tǒng)建模問題進(jìn)行了深入討論。盧劍偉等［7］利用分岔圖及最大李雅普諾夫指數(shù)等，對(duì)考慮隨機(jī)裝配側(cè)隙的齒輪副系統(tǒng)動(dòng)力學(xué)性能進(jìn)行了分析。陳會(huì)濤等［5］建立了單對(duì)齒輪系統(tǒng)純扭轉(zhuǎn)非線性動(dòng)力學(xué)模型，分析了齒輪綜合傳遞誤差波動(dòng)和外部載荷對(duì)系統(tǒng)振幅和動(dòng)態(tài)嚙合力的影響。Velex等［8］對(duì)非線性隨機(jī)參數(shù)系統(tǒng)的振動(dòng)可靠度進(jìn)行了計(jì)算。陳思雨等［9］研究了輪齒隨機(jī)間隙對(duì)齒輪系統(tǒng)動(dòng)力學(xué)響應(yīng)的影響。劉夢(mèng)軍等［10］研究了分析系統(tǒng)非線性隨機(jī)動(dòng)力特性及全局初值特性的方法。

分階式雙漸開線齒輪是綜合了漸開線齒輪和雙圓弧齒輪優(yōu)點(diǎn)的一種新型齒輪［11］，其與普通漸開線齒輪最大的區(qū)別在于工作齒廓由兩段相錯(cuò)的漸開線組成，中間以一段圓弧包絡(luò)線或一段過渡曲線連接，齒頂與齒根兩段漸開線齒廓呈階梯式布置，而普通漸開線齒輪的工作齒廓僅由圓弧構(gòu)成。

筆者建立基于雙漸開線齒輪傳動(dòng)系統(tǒng)的扭轉(zhuǎn)振動(dòng)力學(xué)模型，討論在隨機(jī)振動(dòng)情況下嚙合阻尼比對(duì)雙漸開線齒輪擾動(dòng)及系統(tǒng)動(dòng)力學(xué)的影響。

2 雙漸開線齒輪振動(dòng)模型

建立雙漸開線齒輪振動(dòng)模型，需要根據(jù)齒輪的不同情況，綜合考慮嚙合剛度、輸入力矩、阻尼比、齒側(cè)間隙、激勵(lì)頻率等多種因素的隨機(jī)擾動(dòng)。建模時(shí)不考慮齒面摩擦的情況，采用集中質(zhì)量法。將雙漸開線齒輪振動(dòng)模型簡(jiǎn)化為齒輪副扭轉(zhuǎn)振動(dòng)力學(xué)模型，如圖1所示。

圖1中，雙漸開線齒輪主動(dòng)輪P和從動(dòng)輪G的基圓半徑分別為Rp、Rg，將傳動(dòng)軸、軸承和箱體等的支承剛度和阻尼系數(shù)分別用組合等效值 kpy、kgy、cpy、cgy來(lái)表示。mp和mg分別為主從動(dòng)輪的質(zhì)量，Ip和 Ig分別為主從動(dòng)輪的轉(zhuǎn)動(dòng)慣量，ωp和 ωg分別為主從動(dòng)輪的激勵(lì)頻率，e為齒輪嚙合綜合誤差，km和cm分別為齒輪副嚙合的綜合剛度系數(shù)和綜合阻尼系數(shù)。

齒輪的靜態(tài)傳遞誤差e（t）是客觀存在且隨時(shí)間變化的周期函數(shù)，以嚙合頻率為基準(zhǔn)對(duì)e（t）進(jìn)行傅里葉級(jí)數(shù)展開：

式中：ωh為無(wú)量綱激勵(lì)頻率。

考慮到由e（t）引起的高頻內(nèi)部激勵(lì)和由輸入扭矩波動(dòng)引起的低頻外激勵(lì)，忽略輸出扭矩的波動(dòng)，于是有：

式中：Tp為輸入扭矩；Tpm為輸入扭矩的平均值；Tpn（t）為輸入扭矩的變化值；Tg為輸出扭矩；Tgm為輸出扭矩的平均值。

雙漸開線齒輪振動(dòng)模型具有4個(gè)自由度，分別為主從動(dòng)輪繞旋轉(zhuǎn)中心的轉(zhuǎn)動(dòng)自由度和沿Y軸方向的平移自由度，4 個(gè)自由度的振動(dòng)位移分別為 θp、θg、yp、yg，速度分別為加速度分別為

根據(jù)推導(dǎo)，可以得到系統(tǒng)的分析表達(dá)式為：

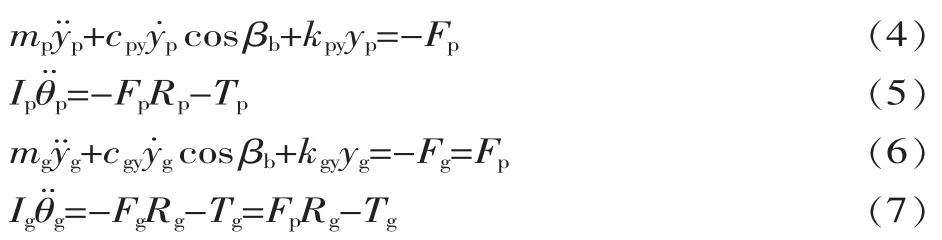
式中：mp、mg、Ip、Ig分別為主從動(dòng)輪的質(zhì)量和轉(zhuǎn)動(dòng)慣量；cpy和cgy分別為主從動(dòng)輪的平移振動(dòng)阻尼系數(shù)；kpy和kgy分別為主從動(dòng)輪的平移振動(dòng)剛度系數(shù)；βb為雙漸開線齒輪的螺旋角；Fg和Fg分別為主從動(dòng)輪受到的外力。

根據(jù)式（4）～式（7），可以推導(dǎo)出：

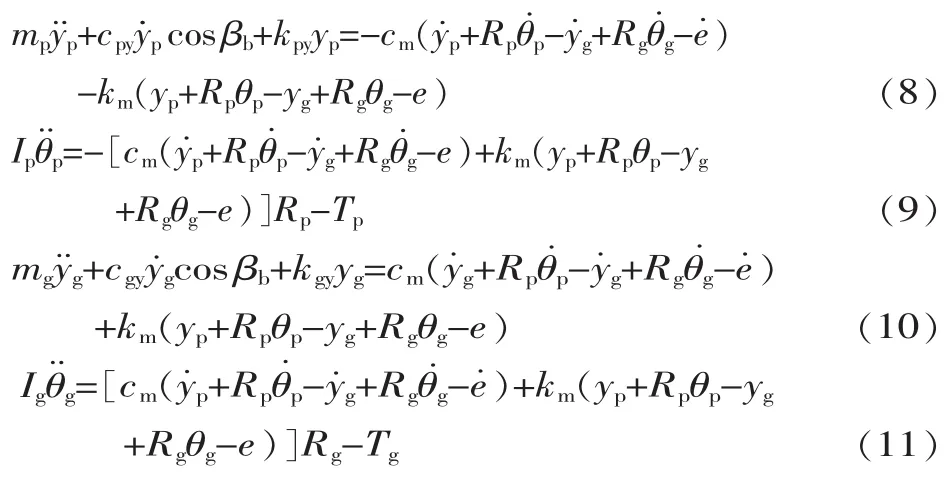
對(duì)式（8）～式（11）進(jìn)行無(wú)量綱化處理，令 x1=yp，x2=為齒輪傳動(dòng)的相對(duì)扭轉(zhuǎn)位移，為齒輪傳動(dòng)的相對(duì)扭轉(zhuǎn)速度，得到狀態(tài)方程：

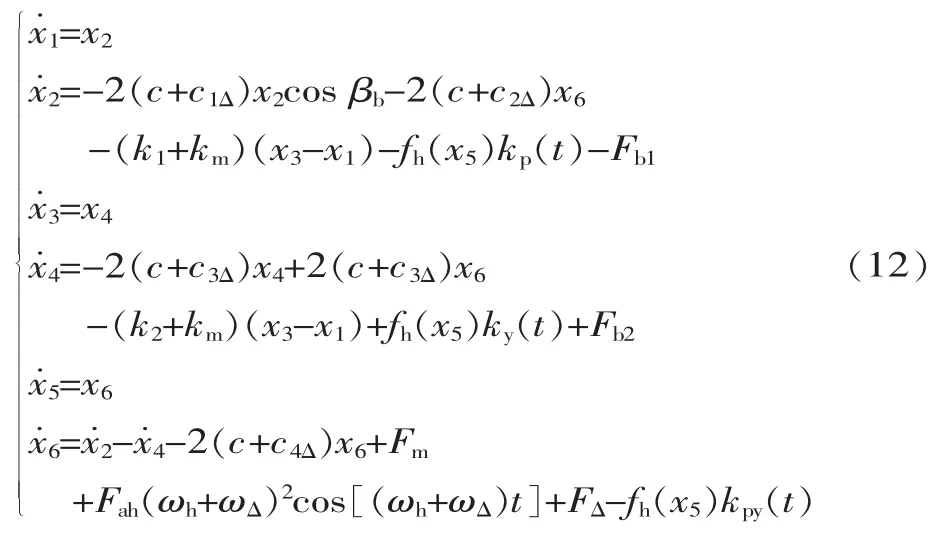
式中：Fb1和Fb2分別為主從動(dòng)輪軸上軸承對(duì)齒輪的無(wú)量綱作用力；k1和k2分別為主從動(dòng)輪的無(wú)量綱嚙合剛度；c1Δ、c2Δ、c3Δ和 c4Δ分別為無(wú)量綱阻尼比的隨機(jī)擾動(dòng)系數(shù)；c為無(wú)量綱阻尼比；Fah為齒輪綜合嚙合剛度誤差；FΔ為無(wú)量綱輸入力矩的隨機(jī)擾動(dòng)量；ωΔ為無(wú)量綱激勵(lì)頻率的隨機(jī)擾動(dòng)因數(shù)；Fm為無(wú)量綱切向平均作用力；kp（t）和 ky（t）分別為主從動(dòng)輪嚙合剛度隨時(shí)間變化的函數(shù)；kpy（t）為主從動(dòng)輪耦合后隨時(shí)間變化的函數(shù)；fh（x5）為齒輪嚙合非線性函數(shù)。

3 非線性動(dòng)力學(xué)特性分析

不同的參數(shù)變量變化使系統(tǒng)的運(yùn)動(dòng)特性變化不同，所以在不同的參數(shù)情況下，系統(tǒng)會(huì)有不同的響應(yīng)。當(dāng)雙漸開線齒輪受到外界擾動(dòng)時(shí)，系統(tǒng)響應(yīng)特性會(huì)隨之發(fā)生變化。為了確定嚙合阻尼比作為隨機(jī)擾動(dòng)因素對(duì)系統(tǒng)動(dòng)力學(xué)性能的影響，首先不加入隨機(jī)擾動(dòng)，分析動(dòng)力學(xué)性能，然后加入隨機(jī)擾動(dòng)，并與無(wú)隨機(jī)擾動(dòng)的系統(tǒng)進(jìn)行對(duì)比，從而得到不同隨機(jī)擾動(dòng)情況下的系統(tǒng)嚙合阻尼規(guī)律。選用變步長(zhǎng)的龍格-庫(kù)塔法對(duì)系統(tǒng)動(dòng)力微分方程逐步積分，選取系統(tǒng)的無(wú)量綱參數(shù)如下：Fah=0.05，ωh=0.34，F(xiàn)m=0.01，F(xiàn)b1=0.2，F(xiàn)b2=0.2，F(xiàn)Δ=0，k1=1.5，k2=1.5，ωΔ=0。取初始狀態(tài) x1（0）=0，x2（0）=0，x3（0）=0，x4（0）=0，x5（0）=0，x6（0）=0，在隨機(jī)狀態(tài)下以嚙合阻尼為分岔參數(shù)，取c=0.18并依次減小嚙合阻尼的大小，令c1Δ=0.012，c2Δ=0.012，c3Δ=0.012，c4Δ=0.012。

將所取數(shù)值代入式（12），利用四階龍格-庫(kù)塔法進(jìn)行數(shù)值分析仿真，從而得到無(wú)隨機(jī)擾動(dòng)和有隨機(jī)擾動(dòng)兩種不同情況的系統(tǒng)動(dòng)態(tài)響應(yīng)，如圖2～圖5所示，圖中X1為無(wú)量綱位移，X2為無(wú)量綱速度。

由圖2～圖5可以看出，當(dāng)c=0.18時(shí)，動(dòng)態(tài)響應(yīng)為近似橢圓形狀，隨機(jī)振動(dòng)對(duì)系統(tǒng)動(dòng)態(tài)響應(yīng)的影響微乎其微；當(dāng)c=0.14時(shí)，動(dòng)態(tài)響應(yīng)為非圓閉合曲線，無(wú)隨機(jī)振動(dòng)的動(dòng)態(tài)響應(yīng)為一條光滑的閉合曲線，而有隨機(jī)振動(dòng)的動(dòng)態(tài)響應(yīng)出現(xiàn)多條纏繞的曲線，此時(shí)可以明顯看出隨機(jī)振動(dòng)對(duì)系統(tǒng)動(dòng)態(tài)響應(yīng)的影響；當(dāng)c=0.07時(shí)，動(dòng)態(tài)響應(yīng)與c=0.14時(shí)基本保持相同，但是纏繞的曲線增多，且有隨機(jī)振動(dòng)的動(dòng)態(tài)響應(yīng)曲線明顯增多，說(shuō)明隨機(jī)振動(dòng)對(duì)系統(tǒng)動(dòng)態(tài)響應(yīng)產(chǎn)生影響。當(dāng)c=0.058 5時(shí)，動(dòng)態(tài)響應(yīng)的圖像為封閉曲線，變化趨于混亂，幅值明顯增大，且有隨機(jī)振動(dòng)的動(dòng)態(tài)響應(yīng)變化幅度相對(duì)明顯。

4 結(jié)束語(yǔ)

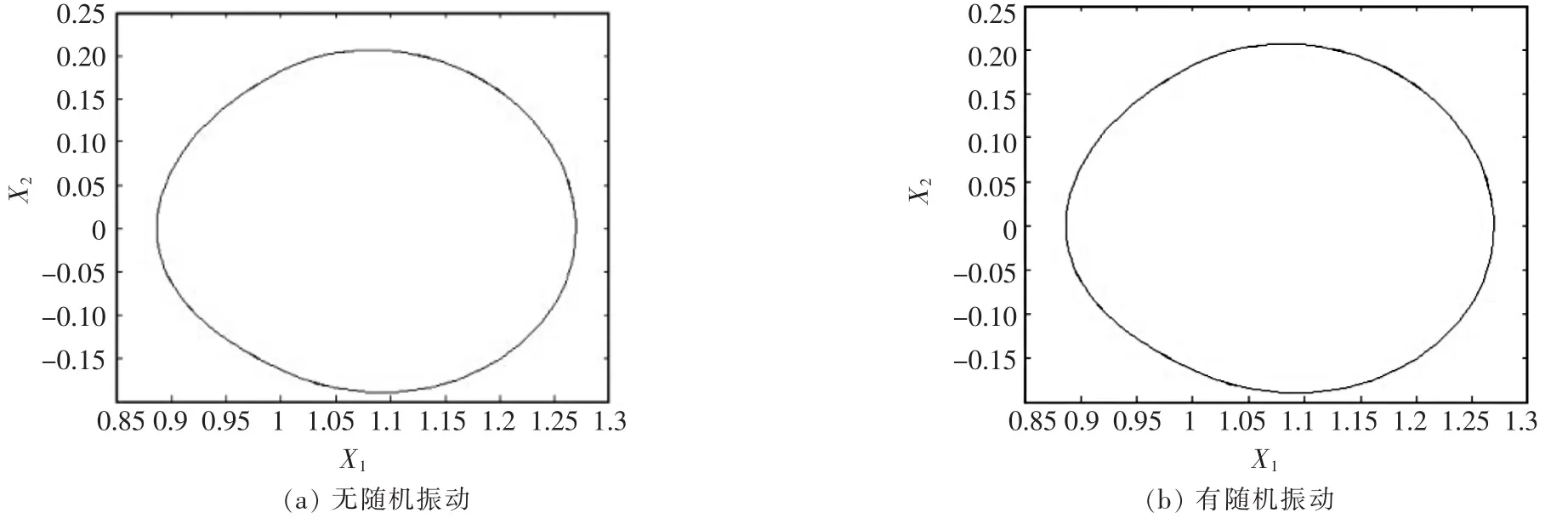
▲圖2 c=0.18時(shí)系統(tǒng)動(dòng)態(tài)響應(yīng)

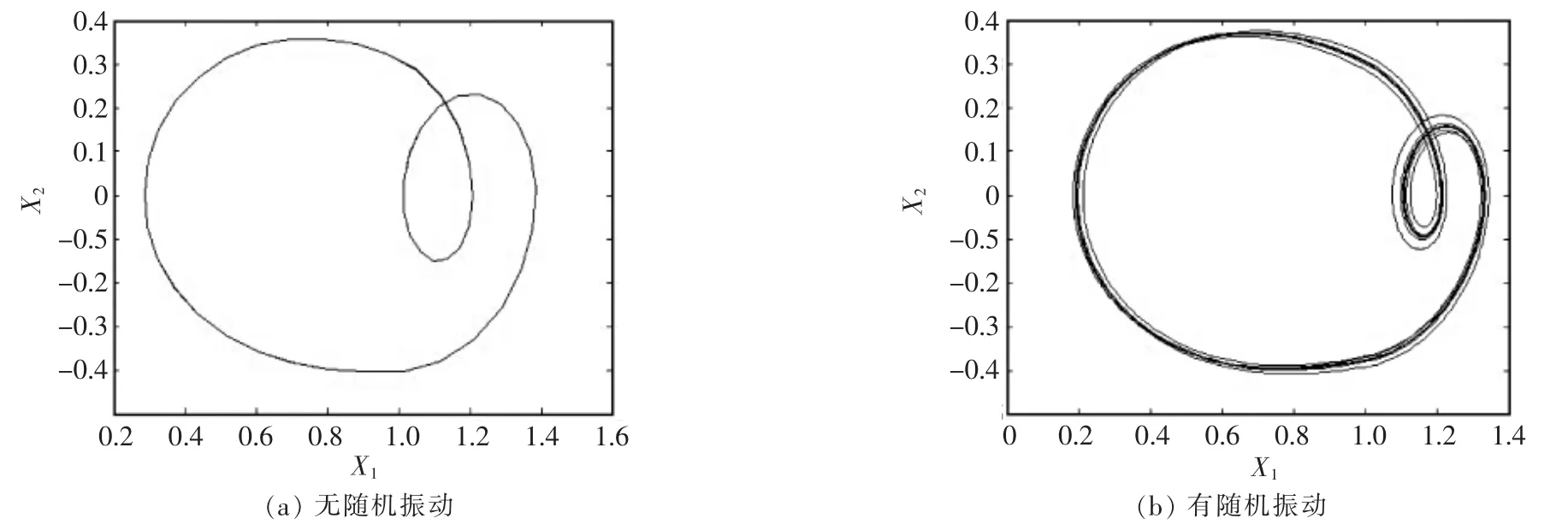
▲圖3 c=0.14時(shí)系統(tǒng)動(dòng)態(tài)響應(yīng)

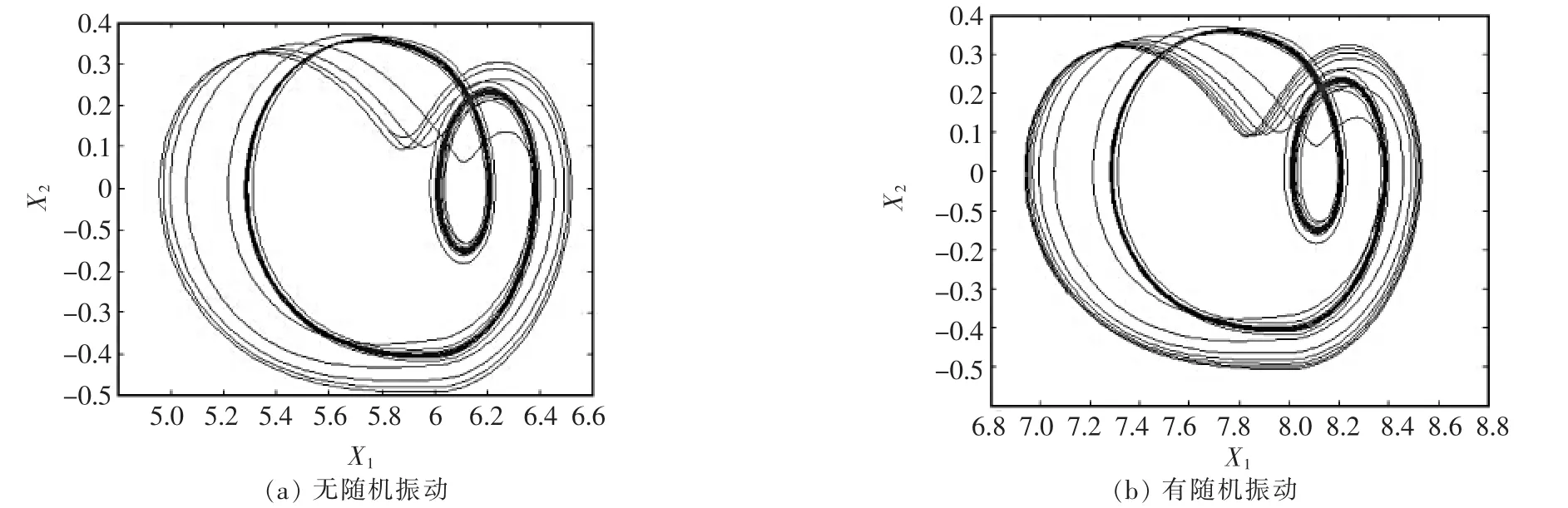
▲圖4 c=0.07時(shí)系統(tǒng)動(dòng)態(tài)響應(yīng)

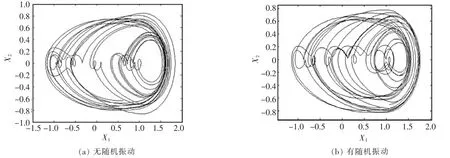
▲圖5 c=0.058 5時(shí)系統(tǒng)動(dòng)態(tài)響應(yīng)

建立雙漸開線齒輪振動(dòng)模型，對(duì)其非線性動(dòng)力學(xué)進(jìn)行分析，在確保無(wú)關(guān)參數(shù)不影響試驗(yàn)的情況下，加入隨機(jī)振動(dòng)進(jìn)行分析，獲得不同嚙合阻尼下的動(dòng)態(tài)響應(yīng)，從而反映不同隨機(jī)擾動(dòng)情況下系統(tǒng)嚙合阻尼的變化規(guī)律［12］。分析結(jié)果表明，隨著嚙合阻尼的變小，動(dòng)態(tài)響應(yīng)愈發(fā)趨于不規(guī)則。有隨機(jī)振動(dòng)的動(dòng)態(tài)響應(yīng)和無(wú)隨機(jī)振動(dòng)的動(dòng)態(tài)響應(yīng)變化趨勢(shì)接近，有隨機(jī)振動(dòng)的動(dòng)態(tài)響應(yīng)相對(duì)變化程度較大，說(shuō)明隨機(jī)振動(dòng)會(huì)對(duì)雙漸開線齒輪傳動(dòng)產(chǎn)生不利影響。影響雙漸開線齒輪傳動(dòng)的非線性因素有很多，實(shí)際使用過程中都是隨機(jī)變化的，需要特別注意。