無先驗信息情況下基于解耦極值荷載效應的橋梁時變可靠性分析
劉月飛,肖青凱,屈 廣,樊學平
(1. 蘭州大學 西部災害與環境力學教育部重點實驗室,甘肅 蘭州 730000; 2. 蘭州大學 土木工程與力學學院,甘肅 蘭州 730000)
0 引 言
橋梁健康監測技術自上世紀80年代至今,主要經歷了兩個階段[1-4]:第1階段是安裝傳感器,獲得監測數據。大量研究主要集中在數據傳送系統、數據壓縮系統、數據恢復系統、數據獲得技術和系統組裝技術等領域,目前已處于成熟階段;第2階段是結構健康監測(SHM)信息的應用。健康監測系統積累了大量監測數據,如何合理地處理這些數據是SHM領域的主要困難之一,目前大量研究主要集中在模態參數識別、損傷識別、損傷評估、模型修正等領域,仍難以有效地預測和評估結構的動態響應行為和可靠性能,因而,合理地應用橋梁健康監測數據修正和預測結構的動態響應行為及可靠性能就成為SHM領域的關鍵問題,可以為橋梁的預防性養護與維修管理決策提供依據和指導,具有重要的理論意義和重大的工程實用價值。
基于SHM的結構可靠性研究已取得一些研究成果:國外,J.CHING等[1]對IASC-ASCE的結構健康監測第2階段Benchmark模型進行了Bayesian分析;Y.Q.NI等[5]提出基于SHM信息的橋梁可靠度評估的概念;M.F.DAN等[6]首次給出基于SHM數據的橋梁可靠度評估的工程實例應用;同時給出基于監測極值的橋梁性能的可靠度評估及預測方法[7],并提出基于Bayesian更新的橋梁可靠度預測方法[8];M.LIU等[9]直接利用SHM系統得到的橋梁活載效應對結構的安全性進行了評估分析。國內,焦美菊等[10]研究了SHM與可靠度評估相結合的橋梁結構性能評估方法;趙卓[11]基于ARMA模型,對長春伊通河橋構件的監測數據進行了建模分析,并評估了相應構件的可靠度;王子健[12]研究了基于SHM數據的車輛和溫度荷載效應組合新方法,并應用于南京長江第三大橋的橋面應力數據,為橋梁可靠性修正提供了合理的信息處理方法;樊學平等進行了橋梁SHM數據的動態線性建模和可靠性修正分析[4]。上述研究均采用耦合信息直接進行可靠性分析,考慮到SHM信號時變性、耦合性以及隨機性等特點,怎樣利用各種荷載效應耦合的SHM信息,建立解耦荷載效應的動態預測模型,進而實現在役橋梁構件可靠性的動態預測需要深入展開研究。
考慮SHM極值應力信號的隨機性與耦合性,采用移動平均法解耦監測極值應力耦合信號,消除信號耦合因素的影響;基于解耦極值應力的分布特性,引入BDLM,構建無先驗信息 (監測誤差方差V未知)的BDLM,對解耦應力信號的變化趨勢進行預測分析;考慮到隨機荷載效應之間可能存在的相關性,引入Kendall秩相關系數進行分析;最后綜合利用SHM 極值應力數據和FOSM方法實現在役橋梁構件的動態可靠性預測。技術路線見圖1。
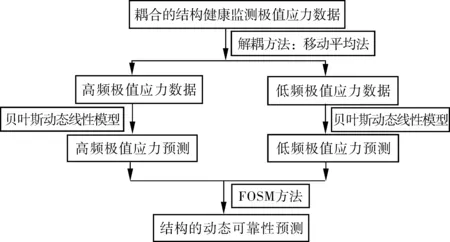
圖1 技術路線Fig. 1 Technical flowchart
1 SHM極值應力信號的一次移動平均解耦方法
利用一次移動平均法提取耦合監測極值應力信號中的低頻信息,進而利用耦合信息減去低頻信息即可得到近似高頻信息。
假設SHM極值應力數據時間序列為:y1,…,yt,…,采用一次移動平均法可求出任意N個連續時間序列點的平均值[13],即:
(1)
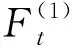
1次移動平均法對低頻極值應力的預測公式為
(2)
利用耦合的極值應力信號減去低頻極值應力數據如式(2)可得高頻極值應力數據。
2 BDLM遞推過程
通常情況下,BDLM的先驗信息很難得到。筆者要考慮在無先驗信息(V未知)的情況下構建貝葉斯動態先驗模型。本模型首先是確定θt的初始信息以及vt,ωt的先驗分布。根據觀測精度φ=V-1的特點,設vt服從正態分布N(0,V),V為未知的常數方差;一般情況下設ωt服從T分布T(0,Wt)。
2.1 BDLM建模方法
分別建立兩個隨機變量(i=1,2)(分別指高頻荷載效應和低頻荷載效應)的BDLM,并對解耦荷載效應分布參數進行遞推分析。過程如下。
監測方程:
yi,t=θi,t+vi,t,vi,t~N(0,V)
(3)
狀態方程:
θi,t=λiθi,t-1+ωi,t,ωi,t~Ti,nt-1(0,Wi,t)
(4)
初始信息:
(θi,t-1丨Di,t-1)~T(mi,t-1,Ci,t-1)
(5)
(φi丨Di,t-1)~Γ(ni,t-1/2,di,t-1/2)
(6)
式中:相關參數的物理意義詳見文獻[13]。
2.2 BDLM遞推過程
1)針對mi,t-1和Ci,t-1,狀態后驗分布信息為:
(θi,t-1丨Di,t-1)~T(mi,t-1,Ci,t-1)
(7)
(φi丨Di,t-1)~Γ(ni,t-1/2,di,t-1/2)
(8)
2)t時刻的狀態先驗分布:
(θi,t丨Di,t-1)~T(ai,t,Ri,t)
(9)
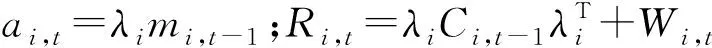
3)t時刻觀測變量一步預測分布:
(yi,t丨Di,t-1)~T(μi,t,Qi,t)
(10)
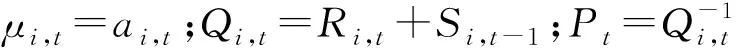
4)t時刻的狀態后驗分布:
(θi,t丨Di,t)~T(mi,t,Ci,t)
(11)
(φi丨Di,t)~Γ(ni,t/2,di,t/2)
(12)
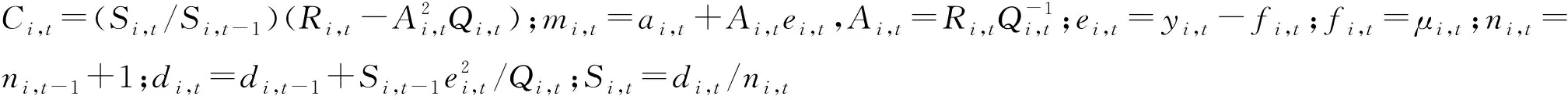
結合文獻[3-4],可得第k步監測值含有95%保證率的預測區間為
(13)
2.3 BDLM相關參數的確定方法
所給出的BDLM中主要相關參數有Si,t-1,Wi,t,mi,t-1,Ci,t-1,ni,t-1,di,t-1,具體確定方法如下。
分布參數Si,t-1=ni,t-1/di,t-1是V=φ-1的一個先驗點估計,在時刻t,φ的先驗均值是E[φi丨Di,t-1]=ni,t-1/di,t-1=1/Si,t-1;狀態誤差的方差Wi,t,由式(14)確定:
(14)
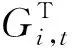
通過t時刻隨機變量的初始狀態信息,可以對mi,t-1和Ci,t-1進行估計。為了進一步探究Γ分布的參數n0對筆者建立的BDLM預測精度變化的影響,分別對參數n0取不同的值進行分析。
3 橋梁構件的動態可靠性預測
3.1 一次二階矩(FOSM)方法
假設抗力R和荷載效應S相互獨立。采用FOSM方法計算結構可靠指標,R和S的平均值和標準差分別為:μR、σR、μS,σS。
極限狀態方程為
g(R,S)=R-S
(15)
可靠指標計算公式為
(16)
3.2 可靠度的計算
橋梁構件極限狀態方程[3-4,7-8,13]為
g(R,S,C,M)=R-S-C-γP(MT+MV)
(17)
式中:R為鋼材的屈服強度;S為鋼材的自重應力;C為混凝土的自重應力;Mt為解耦溫度應力;Mv為解耦車輛應力;γP為修正系數。
結合式(21)可得:
(18)
式中:(μT,σT)、(μV,σV)、(μR,σR)、(μS,σS)、(μC,σC)以及γP的參數物理含義可參考文獻[13]。
4 Ⅰ-39北橋構件監測極值應力數據分析
本算例利用Ⅰ-39北橋[3-4,7-8,13]構件的監測極值應力信號作為實測數據來進行動態可靠性預測分析,此橋為五跨鋼板組合梁橋,總長為188.81 m。
4.1 耦合監測極值應力的解耦處理
采用橫向第2跨跨中梁底的83天極值應力監測數據來進行分析,此數據主要包括極值溫度荷載效應和極值車輛荷載效應,不包括自重荷載效應。耦合極值應力信息如圖2。
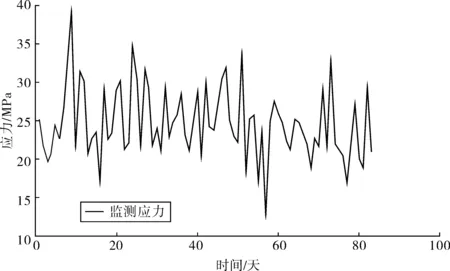
圖2 83天監測極值應力時程曲線Fig. 2 83 days monitoring of extreme stress time-history curve
如圖2,應力時程曲線總體上在25 Mpa波動。對一次平滑處理得到的趨勢項和二次平滑得到的趨勢項[13]進行對比分析,如圖3。
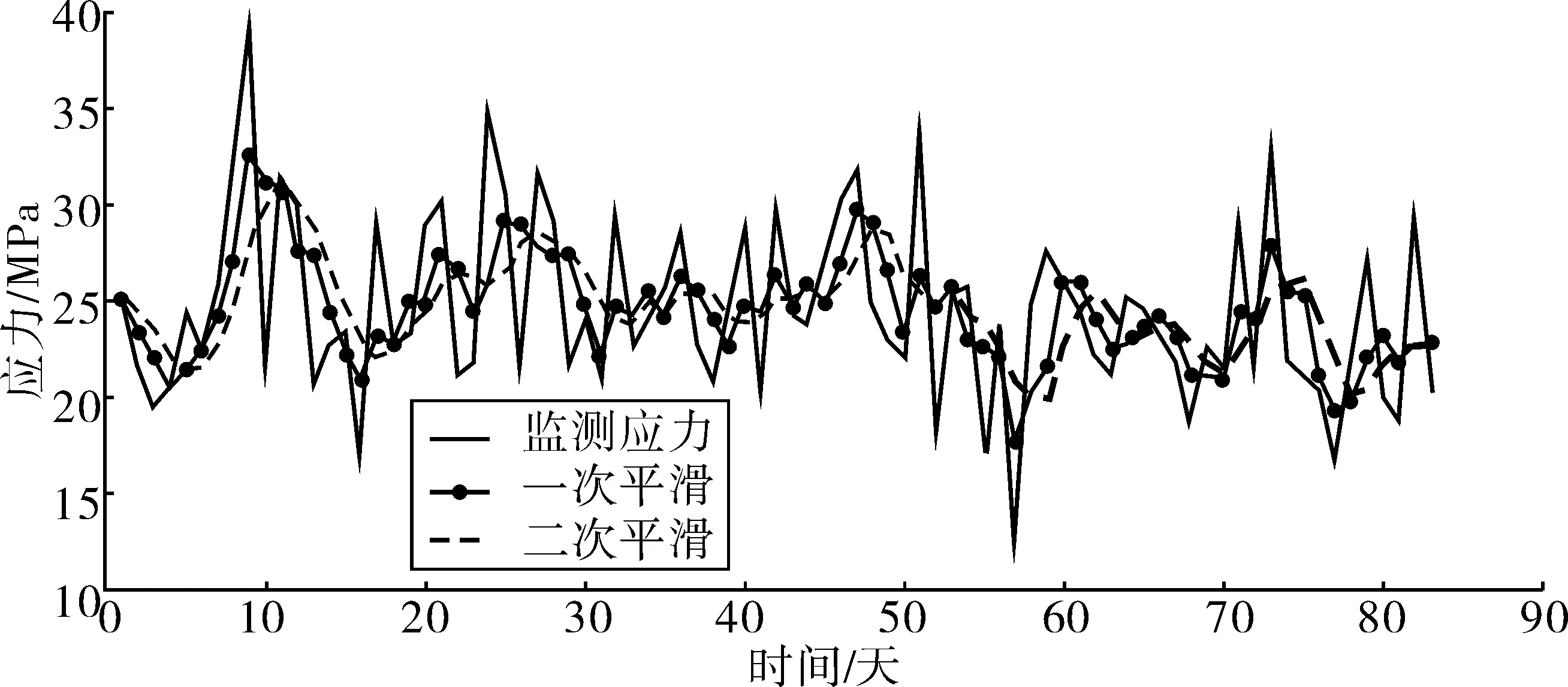
圖3 低頻應力數據提取Fig. 3 Extraction of low-frequency stress data
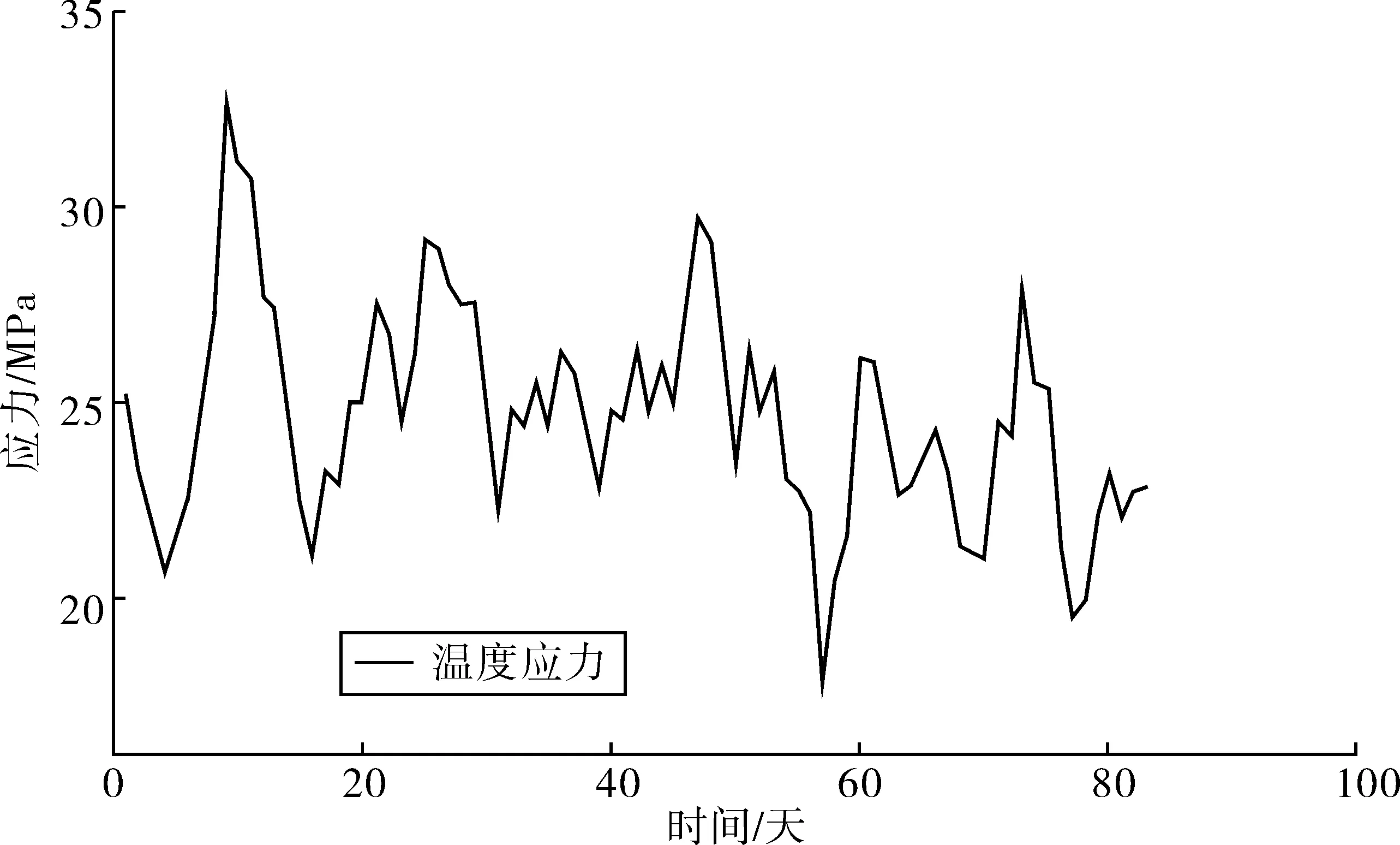
圖4 溫度應力Fig. 4 Temperature stress
由圖3可知,分析兩次平滑后荷載效應的趨勢項,一次平滑趨勢項比二次平滑趨勢項的波動趨勢[13]更加明顯,這樣會有利于監測數據的統計特性得到有效的提取。故筆者采取一次移動平滑方法進行極值應力解耦,解耦結果如圖4,結合圖2可知結構的荷載效應基本上是由溫度荷載造成的,因而溫度應力占耦合荷載效應的主要部分。結合圖5,可知車輛荷載對結構構件的影響很小。
4.2 解耦應力的相關性檢驗
通過SPSS統計軟件對耦合應力信號的秩相關性進行檢驗,結果如表1。
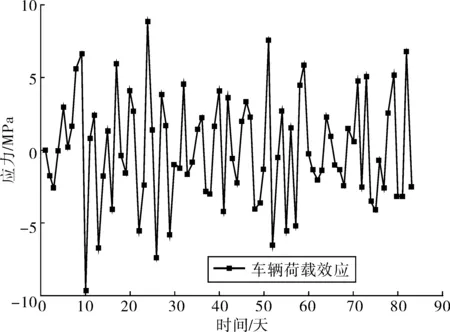
圖5 83天的車輛荷載效應Fig. 5 83 days of vehicle load effect
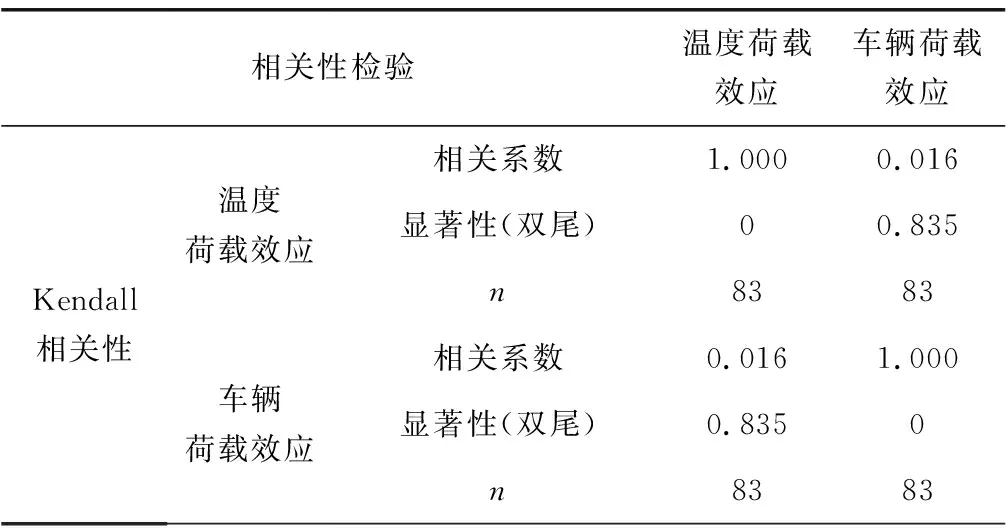
相關性檢驗溫度荷載效應車輛荷載效應Kendall相關性 溫度 荷載效應車輛荷載效應相關系數1.0000.016顯著性(雙尾)00.835n8383相關系數0.0161.000顯著性(雙尾)0.8350n8383
由表1可知,兩個隨機變量的Kendall秩相關系數為0.016,顯著性(雙尾)概率為0.835,故認為解耦應力信號之間是相互獨立的。
4.3 解耦應力的BDMs建模
耦合極值應力經過一次移動平均法的解耦處理,得到83天解耦的溫度應力和車載應力,見圖3和圖4。
下面是確定BDLM的主要概率參數。首先是確定θi,t的初始信息以及vi,t,ωi,t的先驗分布。根據觀測精度φ=V-1的特點,設vi,t服從正態分布N(0,Vi),Vi為未知的常數方差;設ωi,t服從T分布Ti(0,Wi,t)。把解耦的兩個隨機變量經過五點3次平滑處理之后的數據作為初始狀態數據。并基于此估計初始狀態分布信息,如式(21)。
根據式(3)~式(6)可得到Vi未知情況下的貝葉斯動態線性模型(BDLM):
監測方程:
yi,t=θi,t+vi,t,vi,t~N(0,Vi)
(19)
狀態方程:
θi,t=λiθi,t-1+ωi,t,ωi,t~Ti,nt-1(0,Wi,t)
(20)
初始信息:
(θi,t-1丨Di,t-1)~T(mi,t-1,Ci,t-1)
(21)
(φi丨Di,t-1)~Γ(ni,t-1/2,di,t-1/2)
(22)
式中:yi,t為t時刻溫度荷載效應(i=1)和車輛荷載效應(i=2)的監測值;兩個隨機變量的回歸系數λ1=λ2=1;根據以往經驗[3-4]確定初始參數n1,0=n2,0=83(為進一步驗證Γ分布參數ni,0的取值對預測精度變化的影響,對溫度荷載效應的初始參數n1,0取不同的值進行分析,如圖6),根據初始信息由先驗點估計Si,t-1=ni,t-1/di,t-1可得di,t-1;ωi,t為BDLM的狀態誤差。由初始信息可得:Wi,t=-Ci,t-1+Ci,t-1/δi,式中,Ci,t-1由式(21)可得,根據工程經驗取δ1=δ2=0.98。
采用Vi未知情況下的BDLM對83天的解耦應力進行預測:低頻趨勢項應力(主要由溫度荷載造成)的預測結果和預測精度分別見圖7和圖8;高頻應力(主要由車輛荷載造成)的預測結果和預測精度分別見圖9和圖10;由圖7~圖10可知預測得到的溫度荷載效應和車輛荷載效應均能反應監測荷載效應的變化趨勢和變化范圍,而且預測精度隨著監測信息的不斷修正越來越好。
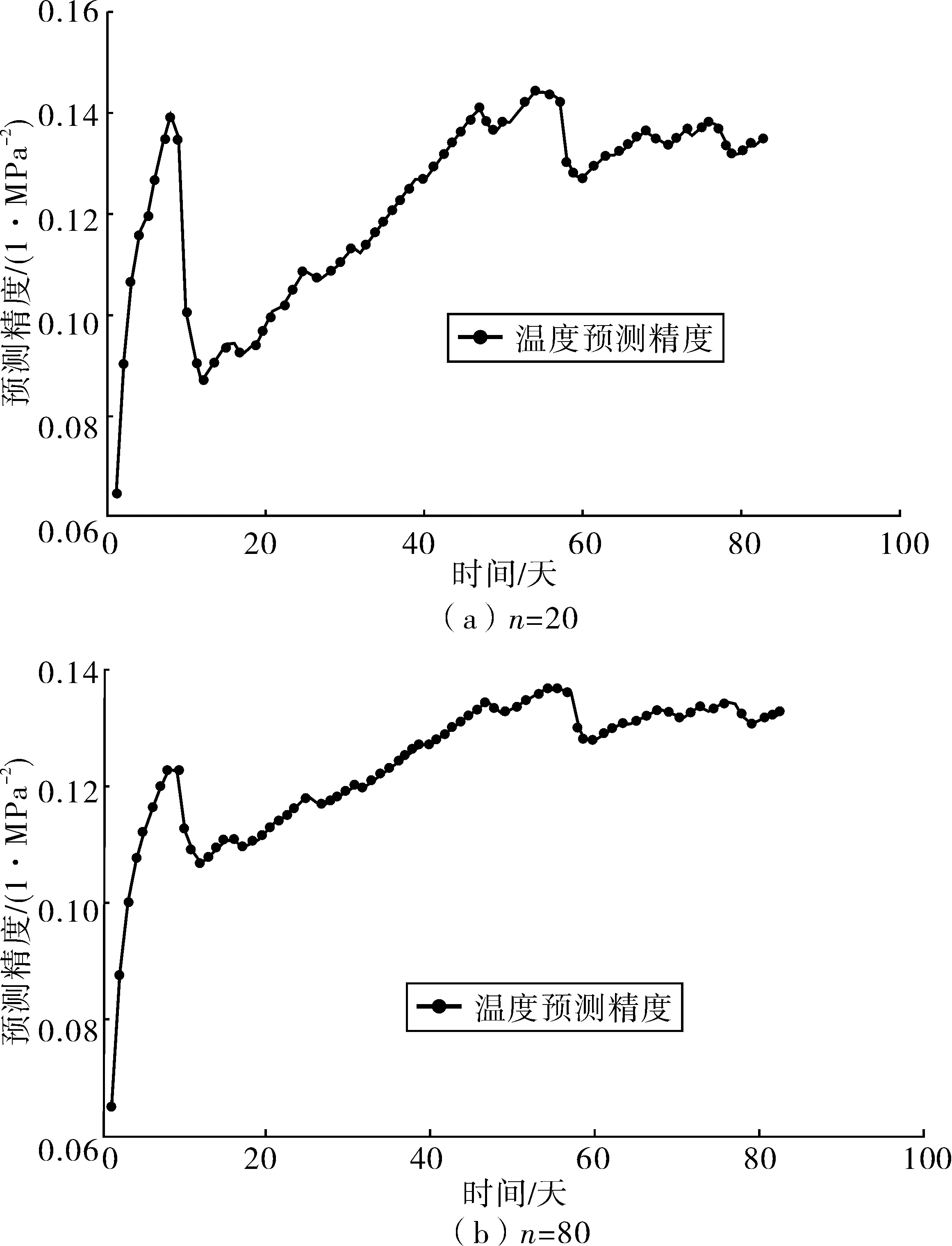
圖6 預測精度隨參數n取值的變化曲線Fig. 6 Thevariation curve of prediction accuracy changing with parameter n
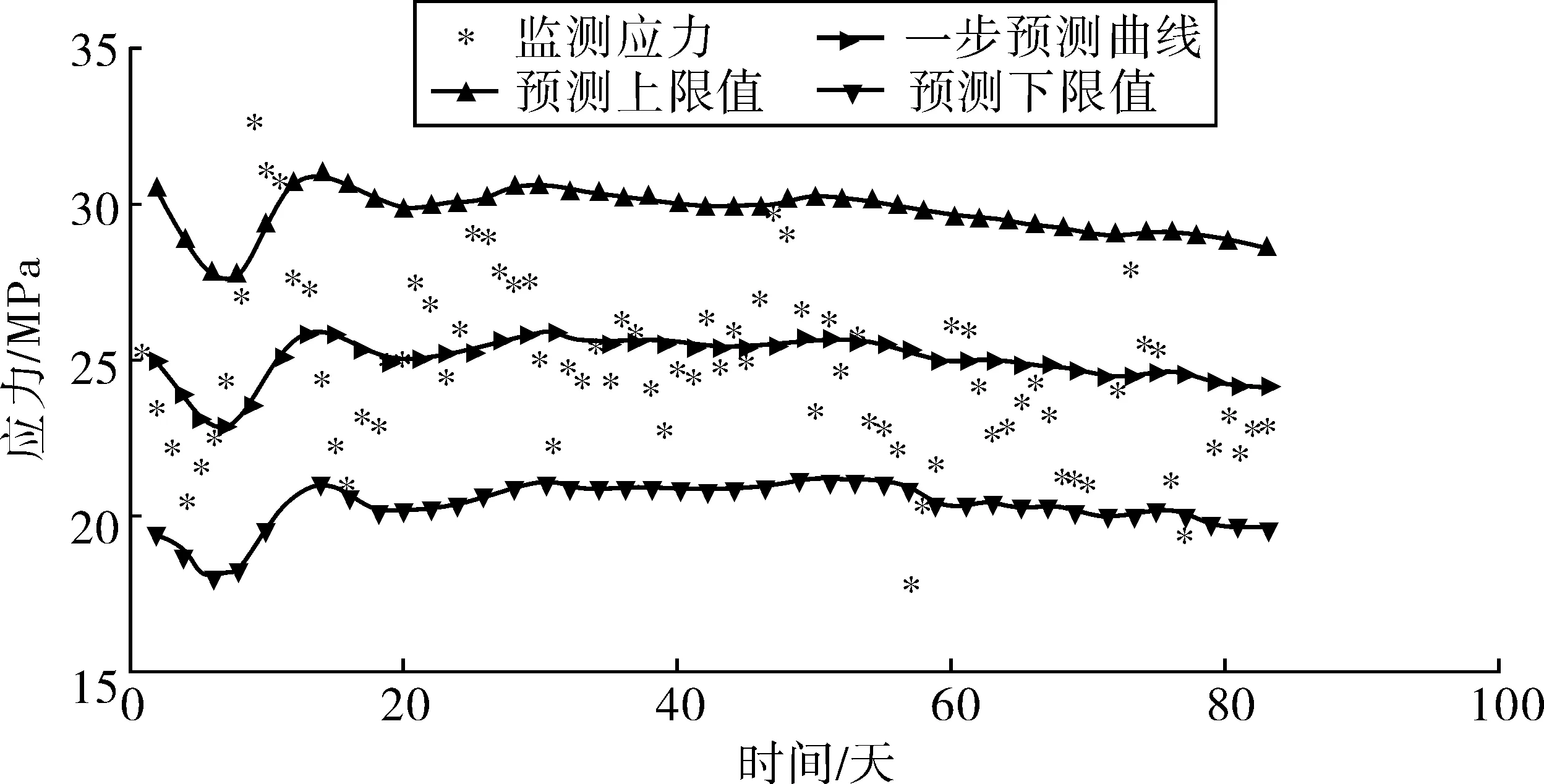
圖7 低頻應力的預測曲線Fig. 7 Prediction curve of low-frequency stress
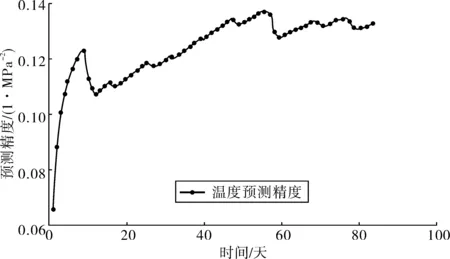
圖8 低頻應力的預測精度變化曲線Fig. 8 Prediction precisionvariation curve of low-frequency stress
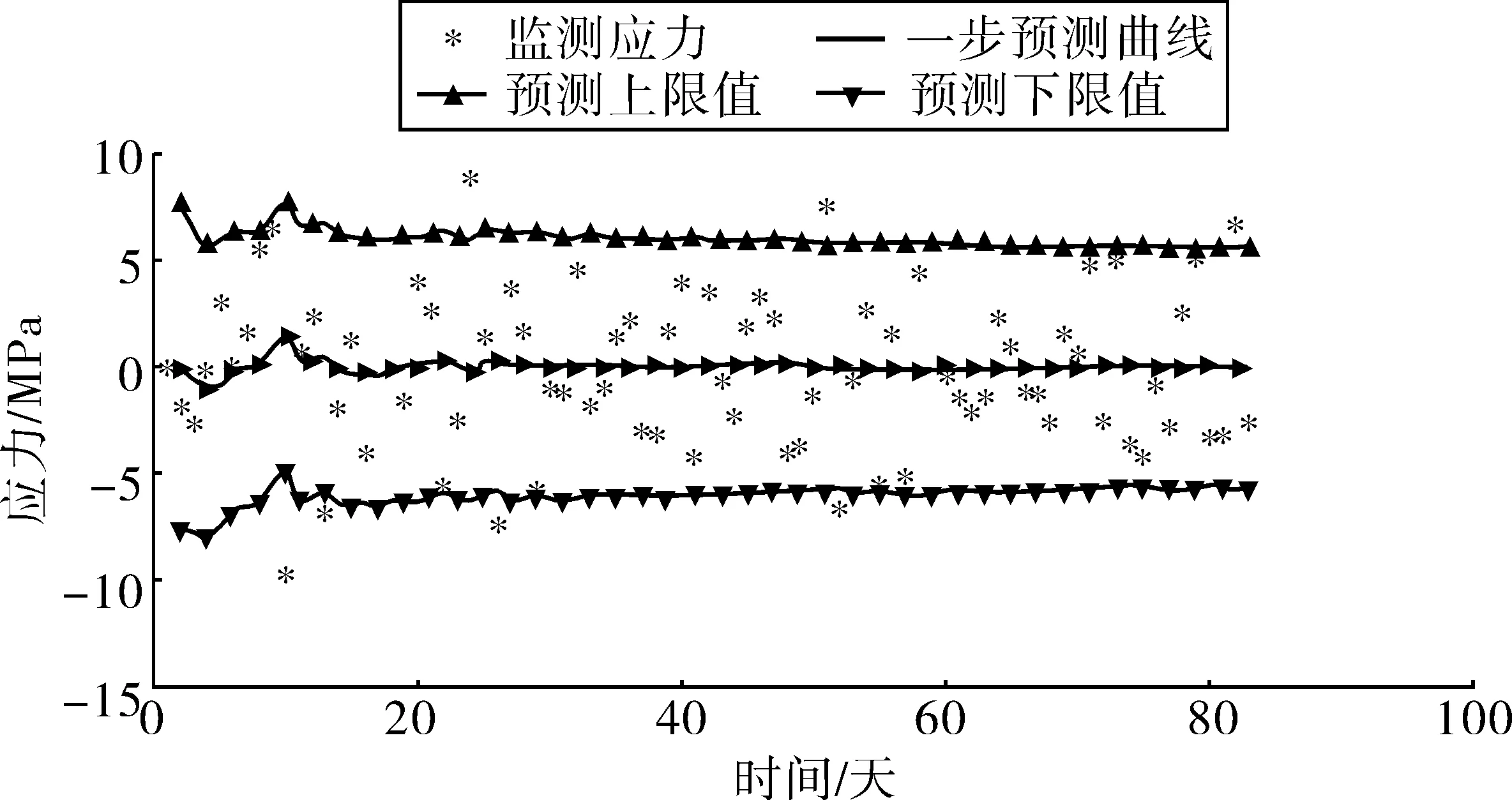
圖9 高頻應力的預測曲線Fig. 9 Prediction curve of high-frequency stress
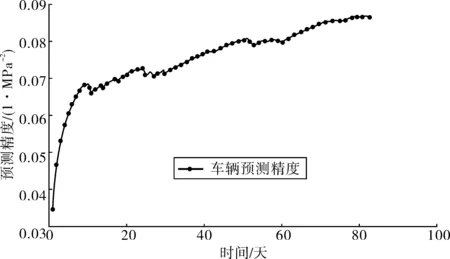
圖10 車輛應力的預測精度Fig. 10 Prediction precision of vehiclestress
為了進一步了解Γ分布參數ni,0的取值對預測精度變化的影響,筆者針對溫度荷載效應的初始參數n1,0取不同的值進行分析,分別令參數n1,0=20,80。由圖10可知隨著n1,0的增大,預測的精度和穩定性越來越好。
4.4 橋梁構件的動態可靠性預測
關于Ⅰ-39北橋的基本設計資料為
μR=380 MPa,σR=26.6 MPa;
μS=116.3 MPa,σS=4.65 MPa;
μS=108.8 MPa,σS=4.35 MPa;
γP=1.15
基于上述實時監測極值數據和基本設計資料,結合式(18)可得:
(23)
采用FOSM方法預測橋梁構件的動態可靠度,并且與實測確定性可靠指標進行比較,見圖11。
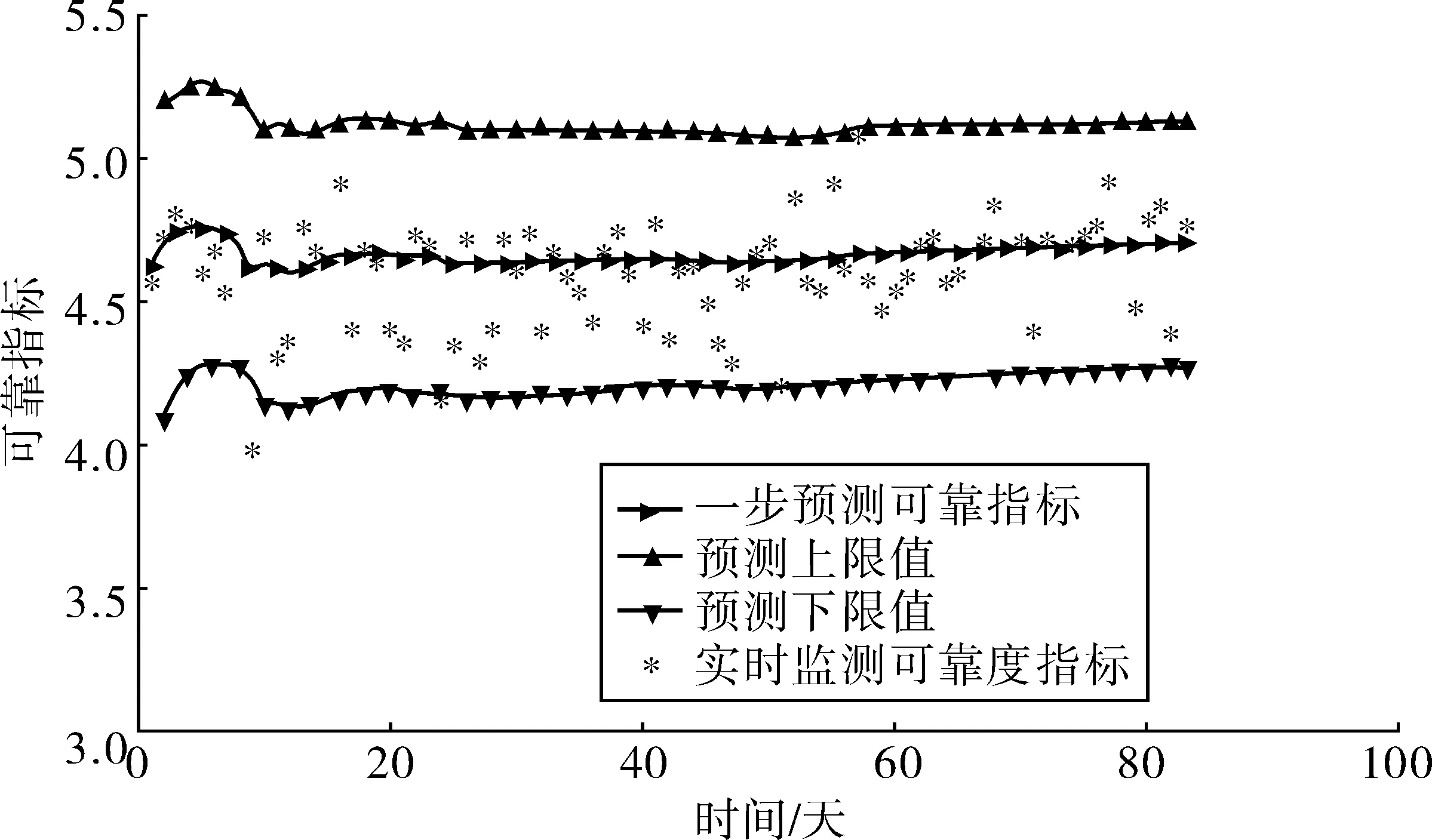
圖11 預測的橋梁結構可靠指標Fig. 11 Predicted structural reliability indices of bridge
由圖11分析可知,基于筆者建立的無先驗信息BDLM和FOSM方法預測得到的可靠指標可以較好解釋實時監測可靠指標的變化范圍和趨勢。
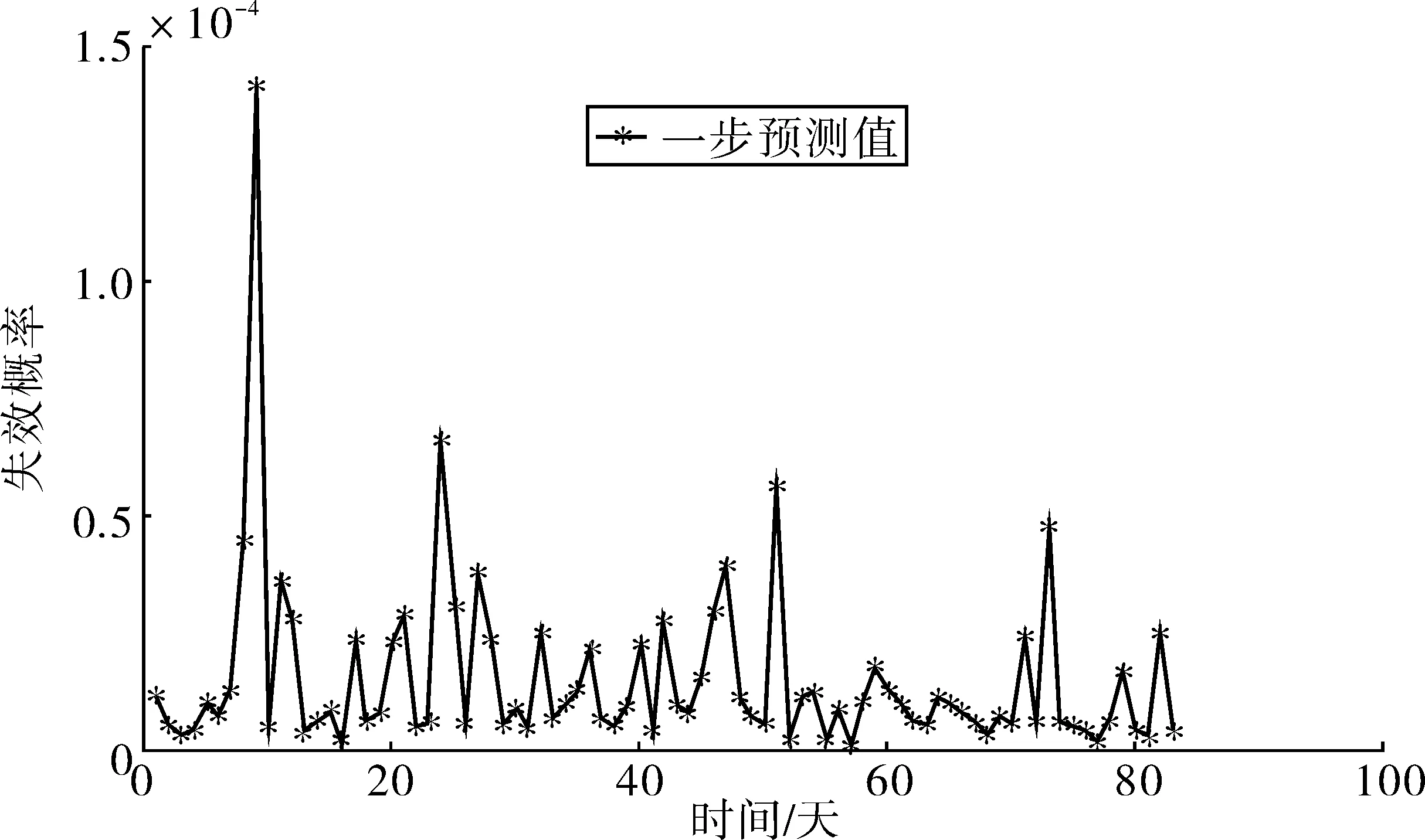
圖12 動態預測的失效概率Fig. 12 Failure probability of dynamic prediction
采用pf=Φ(-β)計算對應失效概率,見圖12。
由圖12可知,Ⅰ-39北橋橫向第二跨結構失效概率小于1.5×10-4,說明橋梁構件處于正常使用階段,安全可靠。
5 結 論
對健康監測極值應力數據進行了解耦分析,消除了耦合因素的影響;引入Kendall秩相關系數,分析耦合應力信號之間的相關性;構建了無信息先驗(V未知)BDLM,預測解耦健康監測數據的變化趨勢;結合可靠度計算方法(FOSM)對鋼板組合梁橋的可靠指標進行了預測分析,得出如下結論:
1)基于解耦監測數據計算橋梁構件可靠指標,可有效消除耦合因素的影響,使計算結果更加合理。
2)無信息先驗BDLM不僅可以合理預估橋梁構件極值應力及動態可靠性,而且可以反映相應數據變化范圍和趨勢。
3)無信息先驗 BDLM的Γ分布參數n0和時間參數是影響預測精度曲線變化的兩個因素:預測精度隨著時間的延長而逐漸增大;預測精度曲線隨著參數n0的增大逐漸趨于平滑,并且在一定范圍內,呈上升趨勢。
4)由預測精度曲線分析可知,無信息先驗BDLM隨著實時監測數據的不斷修正,預測精度越來越高。同時預測精度隨著時間的延長而逐漸增大,說明預測的主觀不確定性越來越小,即預測的客觀性越來越好。

