電梯運行模式的分析及優化設計

羅昱穎 瀘州天立國際學校

引言：隨著社會經濟的發展，高層建筑不斷涌現，而電梯是高層建筑中必不可少的交通設備高效，因此高效的電梯運行模式顯得尤為重要。對于一些上班族和學生黨來說，既想要睡懶覺，又想上班、上學不遲到，那么從家到公司、學校所需等待和乘坐電梯的時間就決定了你是否能準時搭上公交車，是否能躲過遲到的魔爪。本文通過對我們生活中最常采用的隨機運行模式和奇偶層運行模式進行建模分析找到電梯運行模式的優化方案。

1 模型假設及參量描述

1.1 電梯運行規則假設

（1）樓層數為（F+1）（F≥1）

（2）電梯上行時均在第一層達到滿載，最大客容量為P，下行時不再裝載客人

（3）每位乘客在各層下電梯的概率相等，且相互獨立

（4）電梯需要向各層運送的乘客數為c，設各層人數相等，即電梯需要運送的總乘客數為（F+1）c

1.2 電梯運行時間假設

（1）不考慮電梯啟動與制動時的加速和減速過程，即電梯已勻速v運行

（2）電梯運行時在相鄰兩層樓間所經時間為t1

（3）設電梯在每層停留以供乘客出入的時間與乘客量無關，為時間t2（該時間已包含電梯停靠時門的打開和關閉所需時間）

（4）設電梯完成一次全部輸送所需的總時間T

將所用變量列為表一：

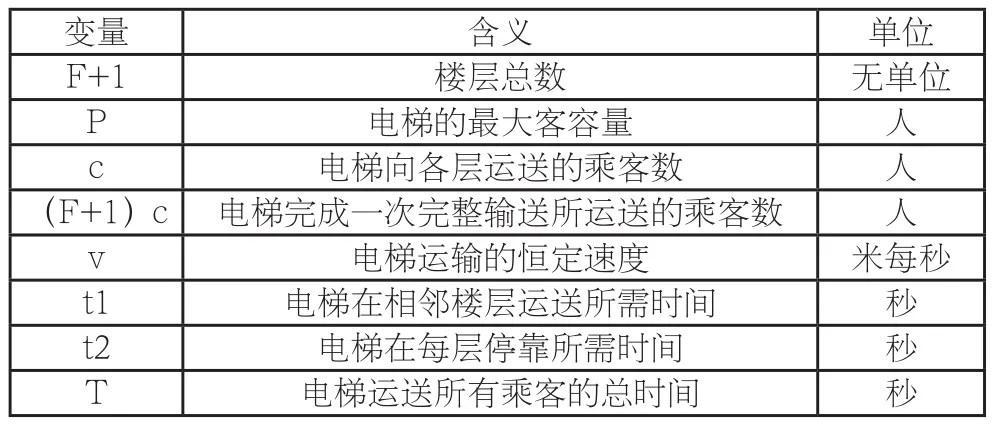
變量 含義 單位F+1 樓層總數 無單位P電梯的最大客容量 人c電梯向各層運送的乘客數 人（F+1）c 電梯完成一次完整輸送所運送的乘客數 人v電梯運輸的恒定速度 米每秒t1 電梯在相鄰樓層運送所需時間 秒t2 電梯在每層停靠所需時間 秒T電梯運送所有乘客的總時間 秒

2 常見電梯運行模式比較

在我們生活中最常見的兩種電梯運行模式則是隨機和奇偶層運行，為簡化描述同時不失一般性，假設有兩臺電梯同時運行。如果一個電梯交通系統能滿足高峰期的交通需求，那么該交通系統就能滿足任意時間段的運輸工作。因此，這里我們考慮如何在電梯使用的高峰期，盡快的將乘客運送至目的樓層，以電梯運送所有乘客的總時間T最短，依據“電梯運行周期與運行總時間之比等于電梯在一個周期內運送的乘客與乘客總數之比”的“比例”原則，對電梯常見運行方式進行評價。

2.1 隨機運行方案

此方案允許電梯上行時在任意樓層停靠，可知兩臺電梯理論的平均運行周期為（2Ft1+Ft2），乘客總數為2P，一個周期內實際運送的乘客數為Fc，所用時間為T.依照上述的比例原則有：

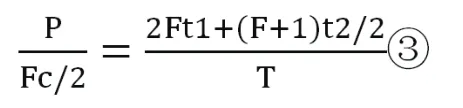
化簡得：

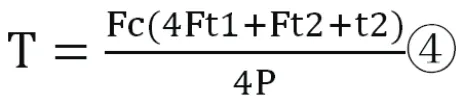
2.2 奇偶層運行方案

該方案要求兩臺電梯向上運行時，一臺停靠奇數層，另一臺停靠第一層和偶數層，現討論F的奇偶性

（1）當F為奇數時，F+1為偶數，運行奇數層的電梯運行周期為（F-1）(2t1+t2/2),運行偶數層的電梯運行周期為【2Ft1+(F+1)t2/2】,所以電梯運送所有乘客的時間即為完成運送至偶數層的乘客所用的時間，仿照①式可得：

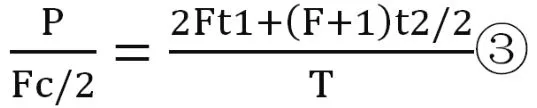
化簡有：

（2）當F為偶數時，F+1為奇數，運行奇數層的電梯運行周期為（2Ft1+Ft2/2）,運行偶數層的電梯運行周期為【2（F-1）t1+Ft2/2】,所以電梯運送所有乘客的時間即為完成運送至奇數層的乘客所用的時間，仿照①式可得：

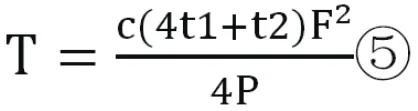
3 電梯運行模式的優化設計

研究了上述兩種運行模式后，我們不妨想象一下如果將樓層分成幾個板塊，再分別由電梯運送，會不會使電梯的運送時間更短，現對電梯新的運行模式作假設：以（Fm+1）（0＜m＜1）層為界分為上下兩段，一臺電梯運行第一層至第（mF+1）層，另一臺則運行第一層，第（Fm+2）層至第（F+1）層，同理可得：

化簡上述兩式得：

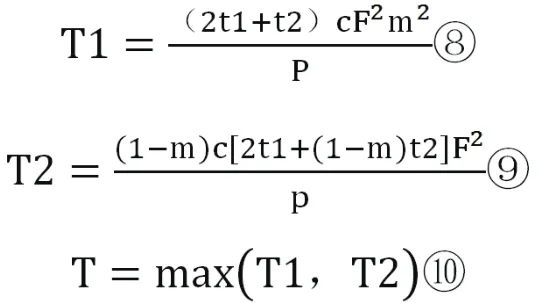
由⑧⑨可知，當m增大時,T1增大，T2減小，所以T1是關于m的增函數，T2是關于m的減函數，令T1=T2,解得

現對m的大小進行分類討論

當m＞n時,T1＞Tn＞T2,T=T1

當m＜n時,T1＜Tn＜T2,T=T2

當m=n時,T有最小值，此時運送所有乘客的總時間最短，即

依據以上對三種模型求得的時間，觀察可得分段運行模式最優。

4 電梯對臨時需求的響應

電梯根據各層的用戶通過面板發出的臨時指令需要做出響應，各樓層發出向上或者向下的指令的概率，在一天中絕大多數的時刻服從均勻概率密度函數，在上下班等高峰段擇更接近于正態分布的概率極大值點。電梯根據任意時間片段內的指令之和，綜合做出對應的運行行為。樓層信息通過各層不同的賦值，可以通過計算判斷對特定的指令，到底是向下運行或向上運行，在有兩臺以上電梯時，是否由同一臺電梯并向上或向下運行至樓層的最大或最小樓層，期間出現的所有樓層信息都加入到電梯對臨時需求的決策內，每到一樓層就判斷臨時的需求中是否有包含該樓層，有則在該層停留，并移除該層需要再停靠的信息，無則繼續運行，運行至最值處，重新從臨時乘梯的需求中找出最值，并判斷向上或向下運行，如此循環。當一段時間內沒有需求信息后，電梯選擇在合適的樓層停靠等待一段時間，并實時的監測是否存在需求。

5 電梯故障響應決策

電梯運行的過程故障率是極低的，可靠性很高，但是設計者必須考慮故障時的處理方法，以避免在極小概率情況下的安全和財產損失。

考慮一個具體的情形：有4部以上的電梯，同時有3部以下的電梯發生了故障。由于電梯總體上上下人是同時進行的，這在現實中可以實現，用不同的時間起點去描述電梯的騎士運行時間，即把電梯記錄故障的時刻設置不同步就可以了，也就是電梯系統運行中可能最多會有3個不同的故障，這時我們的辦法是，對故障發生的樓層進行重要性的大小排序，一次只去解決一個故障，注意在響應這個故障后，電梯已經運行到了新的位置。解決完這個故障后，將這個故障在需要處理得故障清單中清除，然后再對余下剩下的電梯故障重新排序，然后繼續以上的過程，直到所有的故障得以消除或者解決。人數變化時需要等待正在改變人數的電梯運行完才能變化，也就是說，一次只能一個電梯改變其內的人數，其后的電梯運行到任務樓層后只能停在原地等待，改變完的電梯會繼續運動。

比如電梯樓層是0-21層，當鍵盤監測到22以上的輸入時，則不做出任何響應，在0-21層中，只需對監聽到的值進行特定的數學運算就可決定接下去如何運行。

只有一個電梯時發生故障時無法解決電梯的調度的，因此2部以上的電梯不僅是運力的需要，也是故障容錯機制的必要。理論上2部電梯就會很好的運行，并且在電梯變多后，不僅帶來運力的線性提升，還帶來運行控制方法成倍的復雜化。因為一些并發問題使策略容易出現較為復雜的情形，這時總的原則同以上所述。

6 電梯停靠策略

并非所有的時刻電梯在都在同時被需求，實際的情況很有可能是這樣：考慮電梯樓層不特別高，在相對有限的時間內能完成一次完整的運行，電梯只在一個樓層停，這樣乘電梯的每個人都在這個樓層走到自己想去的樓層。那么怎么知道電梯每次在哪個樓層停下來呢？在一樓的時候每個乘客選擇自己的目的層，電梯可以快速的自動計算出應停的樓層。這個應停的樓層應該保證這次乘坐電梯的所有乘客的爬樓梯層數之和最少（包括上下樓）。

7 問題分析及數學建模

該問題本質上是一個數學優化問題。首先為這個問題找到一個合適的抽象模型。從問題的場景中可以看出，有兩個因素會影響到最后的結果：乘客的數量及需要停的樓層。因此，我們可以從統計到達各層的乘客數目開始分析。

假設樓層總共有N層，電梯停在第x層，要去第i層的乘客數目總數為total[i],這樣，所爬樓梯的總數就是∑{total[i]*| i - x|}(i =1 , 2 , …… ,N-1,N)。因此我們的任務就是找到一個整數x使得∑{total[i]*| i - x|}(i = 1 , 2 , ……N-1, N)的值最小。及求函數：

數學求解

方法一：

先考慮最簡單的解決方案，然后在此基礎上進行優化，可以第一層開始枚舉x一直第N層，然后計算如果電梯在第x層停的話所有乘客總共要爬多少層樓。這是最為直觀簡潔的一個解法。

方法二：

現在我們來更仔細的分析一下這個問題，看看怎么樣優化一下。假設電梯停在第i層樓，我們計算出所有乘客總共爬樓梯的層數是Q。如果有N1個乘客想去的樓層在第i層之下，有N2個乘客正好想去的樓層是第i層，有N3個乘客想去的樓層在第i層之上。這個時候，考慮一種具體的情形：如果電梯改停在i-1層，所有目的地在第i-1層以下的乘客可以少爬1層，總共少爬N1層，所有在i層及以上的乘客要多爬一層，總共多爬N2+N3層，這時總共需要爬Q-N1+N2+N3。

反之，如果電梯在i+1層停所有目的地在第i層以上的乘客可以少爬1層，總共少爬N3層，所有在i層及以下的乘客要多爬一層，總共多爬N1+N2層，這時總共需要爬Q+N1+N2-N3層。

可見，當N1＞ N2+N3 時，電梯在第i-1層樓停更好；當N1+N2＜N3 時，電梯在i+1層停更好。其他情況在第i層更好。

通過以上的討論，電梯的運行策略需要考慮的角度較多，可以根據不同的情形建立數學方程，并且從數學的角度進行解決。

8 結束語

本文討論了電梯運行中的規律和可能采取的運行策略。并建立了相應的數學模型，在此基礎上進行了討論和比較，給出了優化運行的方法。