基于LabVIEW的鋰電池SOC預估與參數監測系統

李桂娟， 張持健， 施志剛， 李 亮， 劉 雪

(安徽師范大學 物理與電子信息學院，安徽 蕪湖 241002)

0 引 言

目前，用于荷電狀態(state of charge,SOC)估算的方法主要有開路電壓法、放電實驗法、安時積分法、卡爾曼濾波法[1]以及神經網絡(neural network,NN)法。但是單一使用一種方法都存在諸如精度較低、不能在線預測等問題，文獻[2～4]均采用開路電壓聯合安時積分的方法來預測SOC，并通過不斷地修正SOC值消除累積誤差，預測精度基本都能達到3%左右，但只適合短期預測，長時間會增加估算誤差。文獻[5,6]采用開路電壓法和安時法結合的方法，然后再用卡爾曼法來修正SOC值，減小了預測誤差，增加了運算的復雜性。文獻[7,8]使用反向傳播(back propogation,BP)算法估算SOC，輸入參數為電壓和電流，未考慮溫度對電池SOC的影響，估計誤差大部分處在2 %～5 %之間，誤差較大。

考慮到電池的非線性特征[7]及溫度對SOC的影響，本文采用開路電壓法、安時積分法結合改進的BP算法對電池的SOC進行動態預測，根據采集的實驗數據結合MATLAB進行仿真實驗，結果表明,本文方法預測SOC，誤差絕大多數都在1 %以內，提高了電池SOC的預測精度，驗證了該預測模型的可行性。

1 改進的BPNN預測電池SOC

1.1 SOC預測模型的建立

標準的BP算法在應用中存在不足之處：1)網絡訓練過程中容易遺忘舊樣本；2)容易陷入局部極小值；3)網絡收斂速度較慢。本文采用列文伯格—馬奈爾特(Levenberg-Marquardt,LM)算法來彌補標準BP算法的不足。LM算法是基于數值優化的一種快速算法，結合了梯度下降和高斯—牛頓法。

根據Kolmogorov定理，一個3層的NN具有對任意精度函數的逼近能力，本文采用圖1的預測模型。輸入層包含3個參數，分別為電池的電壓、電流及溫度，其與隱含層之間使用Sigmoid激活函數；輸出層則為電池SOC，使用Purelin線性激活函數；隱含層數通過實驗獲取，亦采用Sigmoid函數。LM算法訓練網絡過程為：

1)計算網絡誤差

(1)

式中tk為期望輸出，yk為實際輸出。

2)修正連接權值

wk+1=wk+[JT(w)J(w)+μI]-1JT(w)e(w)

(2)

式中wk+1為修正后的權值;wk為當前權值;其余項為權值增量，即Δw。

圖1 電池SOC網絡訓練模型

1.2 樣本數據的選取及處理

本文采用的動力電池3.7 V單體鋰電池，其標稱容量為1 500 mA·h，充電限制電壓為4.2 V。根據下位機設計的數據采集電路，將恒流放電電路分別以不同的倍率(0.1，0.2，1，2 C)對鋰電池進行放電實驗，電池的溫度可以直接通過傳感器獲得，將實驗采集到的數據隨機選取一部分作為網絡的訓練樣本，另一部分作為測試樣本。均選取不同倍率下的15組樣板數據作為網絡輸入，SOC為輸出。并對數據歸一化處理

(3)

式中x為實驗測試數據;xmax,xmin分別為實驗測試數據的最大值和最小值，且x′∈[xmin,xmax]。

2 電池SOC預測架構整體設計

2.1 總體設計

本文利用單片機STC12C5A60S2作為主控制器，完成對電池數據的采集。并利用串口協議,將單片機采集的電池參數數據傳輸到LabVIEW上位機，上位機界面將采集的數據通過波形圖實時顯示并存儲。在上位機中設置有報警模塊，當電池參數出現溫度過高、電壓異常等情況時報警，提高了電池的使用安全性。系統結構示意如圖2所示。

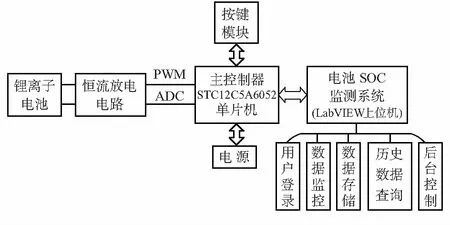
圖2 系統結構示意

硬件部分主要包括主控制器(STC12C5A60S2)、按鍵模塊、電源模塊以及恒流放電電路模塊。單片機用于獲取網絡訓練的電池參數(如電壓、電流、溫度等)數據；按鍵模塊用于控制放電電流；恒流放電電路由場效應管IRF640、運放OP07、采樣電阻器R1等組成，場效應管采取IRF640能較好地通過電壓來實現恒流放電的目的，放電電路如圖3所示。

圖3 壓控恒流放電電路

2.2 基于LabVIEW的監測系統設計

1) 用戶登錄模塊

該模塊作為整個上位機程序的入口，主要實現用戶的登錄管理。該模塊提高了系統的安全性，滿足了一般用戶對實際應用的需求。其登錄界面如圖4所示。

圖4 用戶登錄界面

2)參數監控模塊

該模塊的功能主要有電池參數的采集、顯示、存儲以及歷史數據查看等。其中數據采集部分通過LabVIEW上位機中的VISA資源庫實現對串口數據的讀寫，參數通過波形圖以曲線的形式顯示，數據存儲和數據采集同步進行，以Excel的形式存儲設定的目錄下，如果需要查看某時段的數據，則可以點擊“歷史數據查詢—打開數據”，將已保存的歷史數據回調到顯示界面上，界面顯示結果如圖5所示。

圖5 用戶顯示界面

3 仿真結果與分析

借助MATLAB強大的工具箱來訓練已搭建好的BPNN，將歸一化到[0,1]處理后的電池數據送入網絡進行不斷的訓練與學習。為了加快訓練速度，減小訓練誤差，訓練函數采用LM算法，訓練目標誤差均方誤差(mean square error，MSE)定為10-4，其訓練過程如圖6。

圖6 鋰電池SOC訓練曲線

圖6(a)輸入參數只考慮了電池的電壓和電流，圖6(b)在圖6(a)的基礎上考慮了溫度對SOC的影響，而圖6(c)為用LM算法的網絡訓練結果對比，輸入參數為電池的電壓、電流及溫度，可以看出，相比未考慮溫度參數的標準算法，加入溫度參數后輸出精度要高出2 %左右；采用改進的BP算法一定程度提高了SOC的預測精度，由此也驗證了本文算法的可行性。

保存上述數據，采用本文網絡模型進行仿真實驗，訓練的均方誤差曲線及SOC誤差曲線如圖7、圖8。其中，在500步長內最佳訓練結果為0.000 100 38。

圖7 訓練均方誤差曲線

圖8 SOC誤差曲線

4 結 論

實驗結果證明：采用LM算法來預測電池的SOC具有可行性，在此基礎上考慮了溫度這一參數的影響，不但加快了訓練速度，而且能夠達到較高的精度要求。用本系統所構建的網絡模型來估算電池的SOC，其誤差絕大部分都小于1 %。結合LabVIEW上位機能夠讓用戶更加直觀地了解到電池的參數信息，提高了電池的使用安全性。