MatIab計算在水電站機組盤車及軸線調整中的應用

賈棟林

（中國水利水電第十四工程局有限公司，云南 昆明650032）

1 概述

厄瓜多爾科卡科多辛克雷（Coca codo Sinclair）水電站是我國對外承建的EPC合同中最大的沖擊式水電站建設合同，其電站地下廠房裝設8臺單機容量205 MVA懸式立軸六噴嘴沖擊式水輪發電機組，額定功率187.5 MW，額定轉速300 r/min，飛逸轉速530 r/min，額定水頭604.1 m，是我國目前生產及厄瓜多爾國單機容量最大的立軸沖擊式水輪機組。

機組盤車及軸線調整部位包括：集電環、推力頭、鏡板、轉子、水機軸、轉輪。機組盤車及軸線測量剖面如圖1所示。

2 機組盤車

機組盤車采用在轉子軸端部安裝人工盤車裝置，按順時針方向推動機組轉動部分旋轉。盤車前在每個徑向擺度測量部位的+X、+Y方向設置百分表，在每個軸向跳動測量部位的+Y方向設置百分表。抱緊一半數量的上導瓦，瓦與軸頸間隙控制在0.02～0.04 mm。盤車時啟動高壓油頂起裝置，當鏡板底面與推力瓦接觸面間形成一層均勻油膜后，先連續推動旋轉1圈，然后按標記點進行8等分逐點盤車，并記錄各盤車點停穩后的靜態數據。盤車過程中，在推力頭上放置框式水平儀，推力頭在整個盤車過程中的水平度應≤0.02 mm/m，若有超差，應微調推力瓦受力，使其滿足要求。

3 應用MatIab軟件分析盤車數據

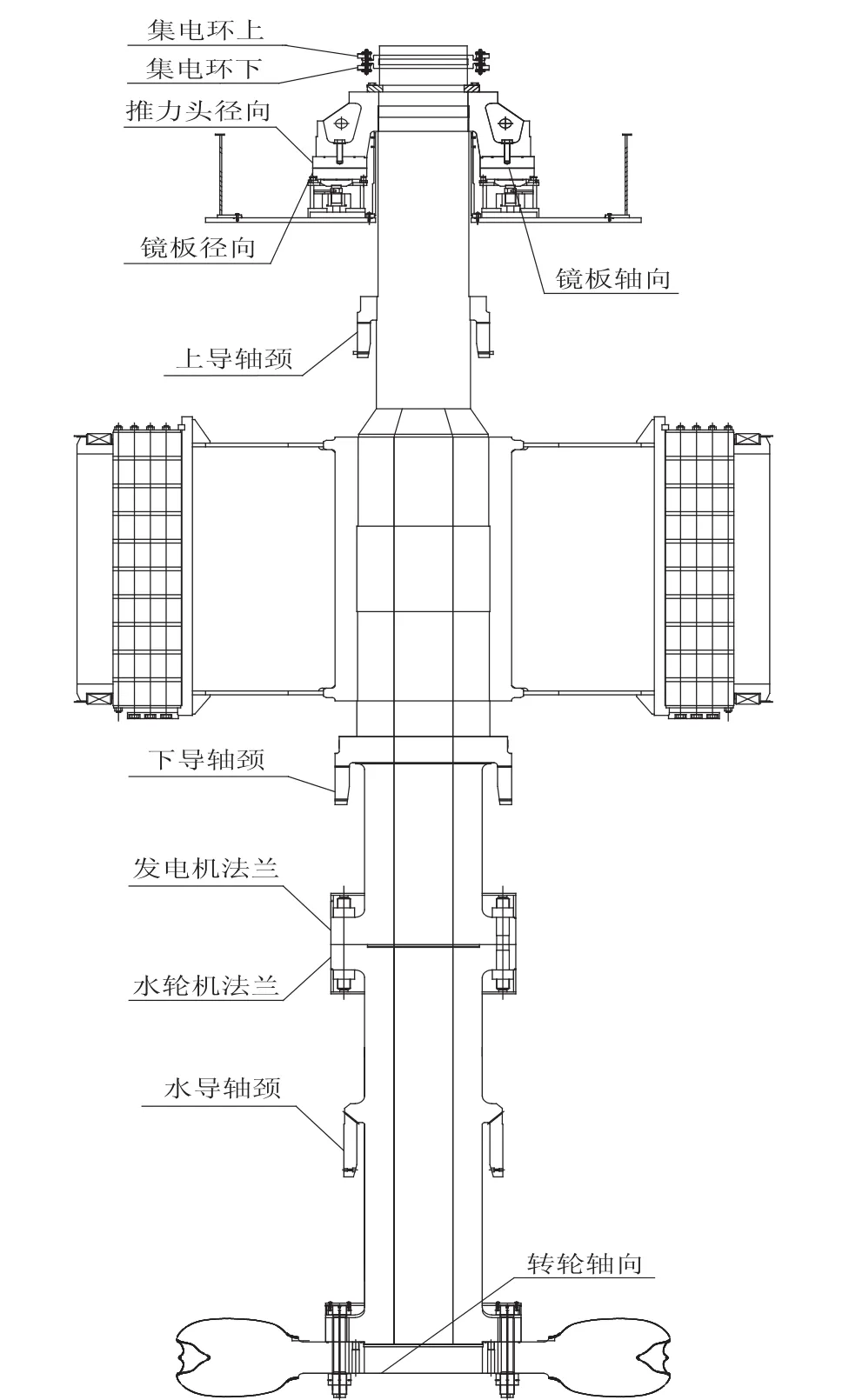
圖1 機組盤車及軸線測量剖面圖

本文以4號機組為例介紹機組軸線數據分析方法，機組盤車數據如表1所示，表中省略了集電環、發電機法蘭、水輪機法蘭及轉輪軸向盤車數據。

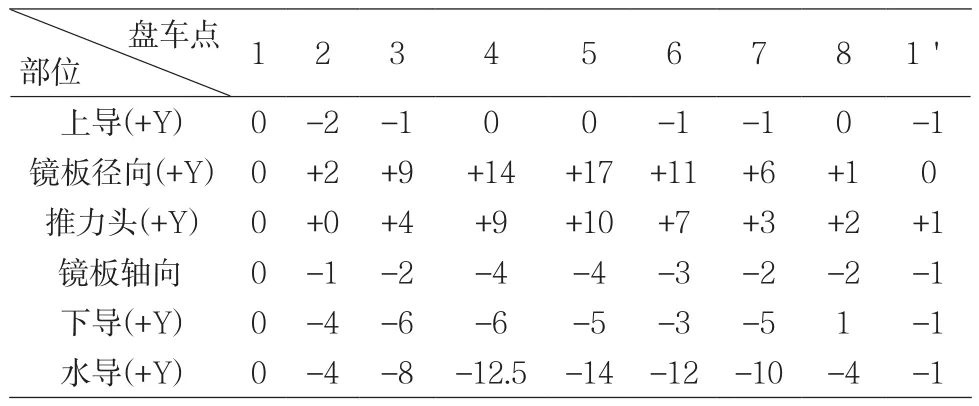
表1 4號機組盤車數據單位：0.01 mm

從表1的數據可以得出鏡板最大擺度為0.08 mm，與推力頭同心度為0.04 mm，滿足后續盤車要求。根據鏡板相對上導的理論擺度為正弦曲線這一概念，假設其曲線為Y=A+B×sin（X+C），根據表1得出鏡板徑向相對上導徑向的擺度如表2所示。

表2 鏡板徑向相對上導徑向的擺度值單位：0.01 mm

然后采用Matlab軟件的lsqcurvefit函數對鏡板相對上導擺度值進行最小二乘非線性擬合，其表達式如下：

clear all；

x=[0,45,90,135,180,225,270,315]；

y=[1,4,10,14,17,12,7,1]；

fun_curve=@(a,t) a(1)+a(2)×sin((t+a(3))× pi/180)；

x0=[0,45,90]；

parameter = lsqcurvefit(fun_curve，x0，x，y)；

A=parameter(1)；

B=parameter(2)；

C=parameter(3)；

subplot(2,1,1)；

plot(x,y,x,fun_curve(parameter,x),'r')；

xlabel(‘角度’)；

title(‘y值’)；

title(‘y=A+B×sin[(x+c)×pi/180]曲線擬合’)；

legend(‘原始曲線','擬合后曲線’)；

subplot(2,1,2)；

fai=0:1:360；

y_value=A+B×sin((fai+C)×pi/180）；

plot(fai,y_value)；

xlabel(‘角度’)；

ylabel(‘Y值’)；

title(‘y=A+B×sin[(x+c)×pi/180]曲線擬合’)；

legend(‘理論曲線’)；

通過擬合程序在Matlab中運行，可以在Matlab工作區中得到 A=8.25，B=-7.89，C=102°。當 a=0°、45°……315°時其理論擺度值為y_value。其測量擺度值與理論擺度值偏差很小，如圖2和表3所示；其理論曲線是正弦曲線，如圖3所示；綜合以上結果，可判斷盤車數據準確，可以作為軸線調整的依據。

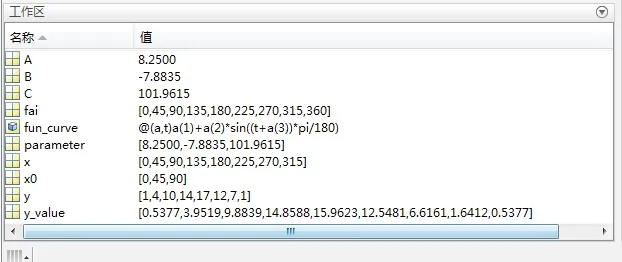
圖2 Matlab工作區顯示計算結果

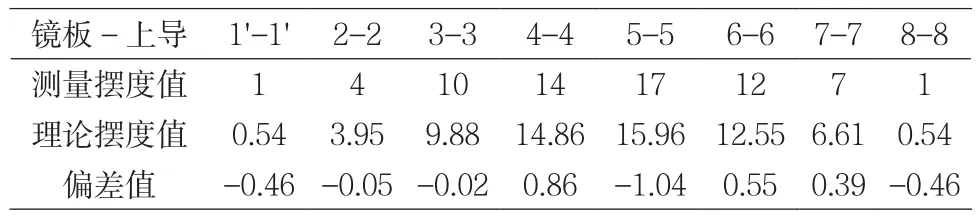
表3 測量擺度值與理論擺度值偏差表單位：0.01 mm

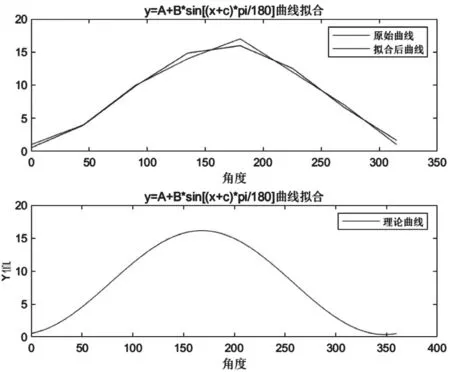
圖3 Matlab機組盤車數據擬合曲線

4 機組軸線調整

當機組整體盤車出現軸線與其旋轉中心線不重合時，計算下導、水導靜擺度，其方法是將下導和水導各點靜擺度值分解成X，Y分量：

x=r×cos（angle×PI/180）

y=r×sin（angle×PI/180）

然后根據擺度值求解下導、水導與機組軸線的理論中心偏差，通過分斷面刮磨發電機推力頭處的鎖緊卡環進行機組軸線的調整，即根據計算發電機推力頭處卡環刮磨量，達到下導和水導處的擺度值盡可能的小。

δ-卡環最大點刮磨量；

D-推力頭的直徑；

Φba-軸線傾斜方向上的最大靜擺度；

L-推力頭距水導處百分表的距離。

5 結束語

伴隨著科學技術的高速發展，Matlab計算已成為工程領域應用最為廣泛的軟件之一，其強大的計算平臺，可以解決實際工程中最優化問題，也可通過對算法的編程實現相應的最優化計算與仿真，能夠有效指導和解決水電站施工中遇到的實際問題，幫助技術人員完成復雜計算與仿真等工作。