溜井放礦過程中貯礦段井壁動態應力分布特征研究

李 偉 劉艷章，2 鄒曉甜 張丙濤

（1.武漢科技大學資源與環境工程學院，湖北武漢，430081；2.冶金礦產資源高效利用與造塊湖北省重點實驗室，湖北武漢430081）

井壁破壞是礦山溜井常見的故障形式之一［1］。根據井壁破壞部位及其成因，溜井井壁破壞可以分為溜礦段沖擊破壞［2］和貯礦段磨損破壞［3］兩類。其中，貯礦段井壁的磨損破壞與井壁動態應力息息相關，通常井壁動態應力大的部位受礦石散體的摩擦力也往往較大。隨著溜井中礦石散體溜放次數的增加，貯礦段井壁的磨損損傷不斷累積，當損傷積累到一定程度時便會導致貯礦段井筒擴徑，甚至是井壁垮塌［4-5］。如能獲悉礦石運移過程中貯礦段井壁動態應力的分布特征，探尋貯礦段各處井壁磨損破壞程度差異的力學機理，對加強貯礦段井壁維護、優化貯礦段結構、提高溜井生產效率具有重要的理論和實踐意義。

溜井中粒徑各異的礦石可以認為是一種散體。礦石運移過程中，由于礦石散體顆粒對溜井井壁的沖擊磨損作用，導致溜井井壁實際所受的側壓力高于其側向靜壓力，這種現象稱為超壓，由超壓現象所引起的實際側壓力稱為側向動壓力，即井壁動態應力。目前，關于散體側壓力的研究主要集中在擋土墻、糧倉、料倉等方面，溜井井壁側壓力的研究則相對較少。陳長冰［6］基于大直徑筒倉，采用靜力平衡法推導了適用于大直徑筒倉的淺埋筒壁橫向靜壓力計算公式；Brown［7］采用砂和大豆進行方形筒倉的裝卸料模擬實驗，測出了筒倉在裝料、貯料、卸料3種狀態下的應力、應變狀態；Khelil和 Belhouchet［8］建立了貯料與圓柱筒倉壁側壓力的平衡方程，獲得了倉壁側壓力的分布特征；Martinez和 Alfaro［9］運用有限單元法，對對稱卸料過程中筒倉的動壓力進行了分析，探討了震動條件下筒倉的力學性能；原方等［10］等基于散體力學，建立了淺圓倉散料側壓力的計算模型，在假設倉壁極值側壓力呈線性分布的前提下，得到了倉壁總側壓力的計算公式。上述關于散體側壓力的分析方法對溜井貯礦段井壁動態應力的研究具有一定的借鑒意義，但由于散體受限狀態不同，物理力學性質亦存在差異，因此上述研究成果并不完全適用于溜井。

本研究以金山店鐵礦主溜井為工程背景，推導貯礦段井壁動態應力的理論計算公式并計算不同高度處的井壁動態應力理論值；采用數值模擬及相似試驗模擬主溜井放礦過程，對貯礦段井壁不同高度處的動態應力值進行分析；將理論計算、數值模擬、相似試驗所得井壁動態應力及相似試驗所得井壁磨損分區范圍進行對比，驗證理論計算公式及研究結果的合理性。

1 金山店鐵礦主溜井貯礦段概況

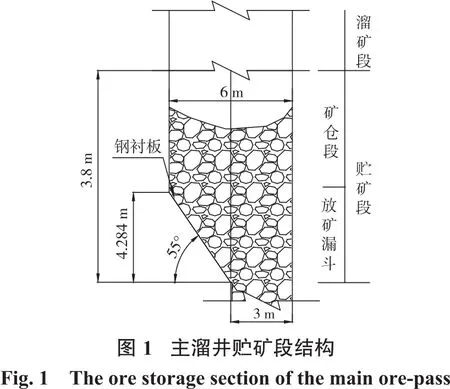
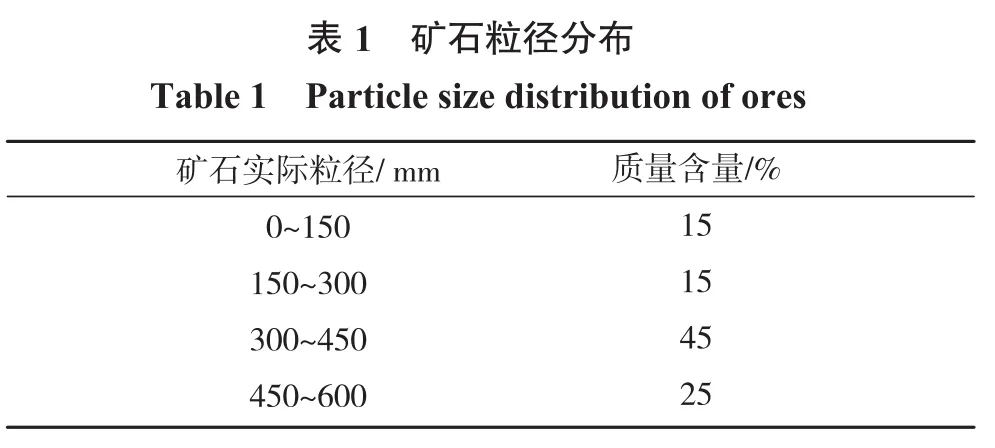
金山店鐵礦-410 m至-480 m水平主溜井主要包括溜礦段和貯礦段2部分。其中，貯礦段高38 m，主要由礦倉段和放礦漏斗構成，如圖1所示。上部的礦倉為圓形斷面，斷面直徑D=6.0 m，采用C30混凝土支護井壁；下部的放礦漏斗為圓口單側斜漏斗，放礦漏斗角為55°，上口直徑D=6.0 m，下口（放礦口）直徑d=3.0 m，采用鋼襯板支護漏斗壁。礦石密度約為3 320 kg/m3，含水率控制在3%～5%，儲礦高度一般為35.0 m，放礦時通常在井內保留2/3的礦石作為緩沖層，以保護下部放礦設備的安全。主溜井內的礦石塊度控制在600 mm以內［11］，粒徑分布如表1所示。

2 貯礦段井壁動態應力理論計算

溜井放礦過程中，貯礦段井壁不同高度處所受動態應力的大小不盡相同，如何定量反映礦石流動過程中貯礦段井壁各處動態應力的分布特征，是分析貯礦段井壁磨損破壞程度差異的關鍵。目前，人們廣泛采用Janssen公式［12］計算類筒倉結構單位面積上的垂直靜壓力，如式（1）所示。

式中，Pv為距容器底板距離為h的測點所在截面上的垂直靜壓力，Pa；γ為貯料的容重，N/m3；R為筒倉半徑，m；f為倉壁與貯料顆粒間的摩擦系數；H為貯料高度，m；h為測點到容器底板之間的垂直距離，m；k為側壓系數。

側壓系數k是依賴于摩擦系數f的無量綱系數，通常由其實用公式算得，如式（2）。當摩擦系數f在0.292～0.625范圍內時，λ的取值范圍為1.00～1.15［13-14］：

式中，φ為散體顆粒的內摩擦角，（°）。

倉壁的水平壓力（側向靜壓力）Ph則通過垂直靜壓力Pv乘以側壓系數k來求解，如式（3）所示。

假設溜井放礦漏斗所采取的圓口單側斜漏斗結構對溜井井壁側向靜壓力影響較小，則可利用式（3）計算溜井井壁的側向靜壓力。然而，由于礦石對井壁的沖擊作用，導致溜井井壁實際所受的側壓力（即側向動壓力）往往高于其側向靜壓力。基于此，在溜井井壁側向靜壓力計算式（3）中引入超壓系數η［15］，推導出因超壓現象引起的井壁側向動壓力（即動態應力）Pd的計算公式見式（4）。

式中，超壓系數η是指井壁側向動壓力（即動態應力）與靜壓力之比［16］，通常η＞1且與井壁位置無關。

金山店鐵礦主溜井內礦石的容重γ為33.20 kN/m3，井筒半徑R為3 m，儲礦高度H為35 m。關于井壁與礦石散體間的摩擦系數f及內摩擦角φ，文獻［11］中作者通過制作半側井筒配合地質羅盤進行摩擦系數測定試驗，最終測得井壁與礦石散體間的摩擦系數f為0.56，采用三軸剪切試驗測得礦石顆粒的內摩擦角φ為31.8°［11］。根據摩擦系數f的大小，取λ的值為1.1，將λ和摩擦系數f帶入式（2），算得側壓系數k為0.52。超壓系數通常在1～1.5之間，本研究取超壓系數η為1.3［16］。根據金山店鐵礦主溜井貯礦段結構特征，以放礦口所在平面為h值（即測點高度）的零點基準面，在放礦漏斗以上區域，分別對h值為5 m、10 m、15 m、20 m、25 m、30 m高度處的動態應力值進行計算，根據式（4）算得貯礦段井壁不同高度處的動態應力理論值如表2所示。

3 貯礦段井壁動態應力數值模擬

3.1 數值模擬模型構建

根據工程實際建立如圖2所示的主溜井貯礦段放礦數值模型，其中，以溜井貯礦段對稱面所在平面為典型剖面，放礦漏斗斜壁側以上的井壁稱為貯礦段左壁，放礦漏斗直壁側以上的井壁稱為貯礦段右壁，后文提到的溜井貯礦段左壁與右壁含義均與此處相同。貯礦段井壁及礦石顆粒分別由數值模擬軟件中的墻體和單位厚度圓盤生成，礦石含水率由礦石顆粒間的粘結強度及摩擦系數間接表示，主溜井貯礦段結構參數、儲礦高度及礦石粒級均與實際參數一致。

3.2 數值模型微觀參數賦值

文獻［11］中，作者采用文獻調研及散體剪切試驗等方法，得到了礦石顆粒的微觀力學參數，同時測得了礦石顆粒與井壁間的摩擦系數。本研究通過對主溜井內礦石顆粒現場調研資料的分析，結合文獻［11］中測定的礦石顆粒微觀力學參數及摩擦系數等，確定的數值模型微觀力學參數如表3所示。

3.3 數值模擬結果分析

結合理論計算時所取測點高度，分別在圖2所示主溜井貯礦段放礦數值模型的左壁與右壁，距離放礦口5 m、10 m、15 m、20 m、25 m、30 m等高度處設置動態應力監測點，對放礦過程中貯礦段井壁動態應力的變化情況進行監測。考慮到放礦過程中礦石顆粒流動的不連續性及礦石顆粒與貯礦段井壁之間接觸的不連續性，監測數據以放礦過程中自放礦開始貯礦段井壁所受動態應力的極大值為準。不同高度處溜井貯礦段左壁與右壁動態應力的分布情況如表4所示。

表4中，放礦漏斗之上同一高度處，溜井貯礦段左壁與右壁動態應力值之間盡管存在差異，但相差不大，兩者間的最大差值為21.1 kPa，相對于最大動態應力244.6 kPa而言差值不足8.6%；溜井貯礦段左壁與右壁井壁動態應力的均值與其距放礦口的距離呈負相關，放礦口以上（5.0 m，15.0 m）范圍內，井壁兩側動態應力的均值均超過了230 kPa；放礦口以上（15.0 m，30.0 m）范圍內，井壁兩側動態應力的均值均不足208 kPa。

4 貯礦段井壁動態應力相似試驗

4.1 相似試驗裝置

根據工程實際采用C30混凝土，按相似原理取尺寸相似比為40、井壁材料相似比為1制作溜井貯礦段井筒，礦石材料相似比為1，應力相似比為40，放礦漏斗由鋼材料制成［17］。結合數值模型中所取測點位置，在現有溜井放礦相似試驗裝置［15］基礎上，以溜井放礦口為零點基準面，根據相似比，在溜井左壁與右壁，每隔125 mm（對應實際距離5 m）高度對稱預留一對應變傳感器埋設孔，并埋入LY-350應變式土壓力盒，總計埋置12個，配合XL2101G程控電阻應變儀進行不同測點處的井壁應變值監測。應變式土壓力盒的埋置方案如圖3所示，埋置了應變式土壓力盒的溜井放礦相似試驗裝置如圖4所示。

4.2 相似試驗礦樣制備

試驗用礦石取自礦山生產現場，根據金山店鐵礦主溜井內實際的礦石粒級分布（見表1）及試驗相似比，計算得到試驗用礦石粒徑如表5所示。將破碎、篩分后的礦樣烘干，按3%～5%的含水率計算水的質量并加入烘干礦樣中，根據質量配比重新配制礦量。

4.3 相似試驗結果分析

試驗用礦石配備就緒且設備連接檢查無誤后，接通應變儀電源并設置好相關參數，將配備好的礦石顆粒注入溜井貯礦段相似試驗模型中至875 mm（對應數值模擬35 m）處。考慮到礦石顆粒在自重影響下的壓密流動及應變儀的預熱過程，礦石注入完畢后需靜置1 h。1 h后將系統初始應變值清零，打開溜井放礦口底板放礦的同時點擊自動連續采集，采集時間間隔為0.2 s。同組試驗重復進行3次，分別取每次試驗中各測點處各自應變監測值的極大值，將各測點3次極大值的平均值作為各測點處的應變監測值，根據式（5）帶入應變儀的率定參數k和c，將應變監測值轉換為對應的動態應力值。

式中，σ為應力值；ε為應變儀的應變監測值；k和c為應變傳感器的率定參數。

根據式（5）將溜井貯礦段井壁各位置處的應變監測值換算成相應的應力值后，再通過應力相似比將應力監測值換算成實際值，換算后的井壁動態應力實際值如表6所示。

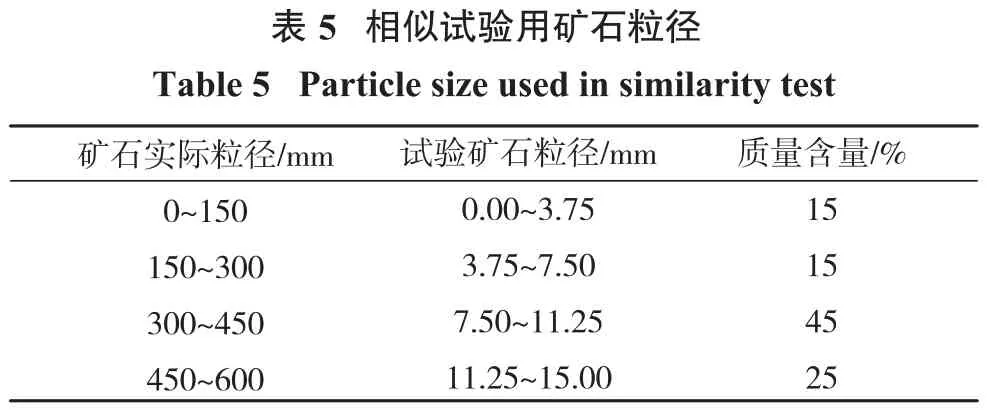
表6中，放礦漏斗之上同一高度處，溜井貯礦段左壁與右壁動態應力值相差不大，兩者間的最大差值為33.0 kPa，相對于最大動態應力256.9 kPa而言差值不足12.8%，溜井左右兩側井壁的磨損程度及磨損分區位置基本一致；溜井貯礦段左壁與右壁動態應力的均值與其距放礦口的距離呈負相關，放礦口以上（5.0 m，15.0 m）范圍內，井壁兩側動態應力的均值均大于229 kPa，井壁嚴重磨損［17］；放礦口以上（15.0 m，30.0 m）范圍內，井壁兩側動態應力的均值均不足185 kPa，井壁輕微磨損［17］；井壁動態應力越大的部位，井壁磨損程度也越重。

5 貯礦段井壁動態應力對比分析

為了驗證貯礦段井壁動態應力理論計算公式及研究結果的可靠性，將理論計算、數值模擬、相似試驗所得井壁動態應力分布特征進行對比，對比結果如表7所示。其中，數值模擬和相似試驗中放礦漏斗以上同一高度處，由于溜井貯礦段左壁與右壁動態應力相差很小，因此取左壁與右壁動態應力的平均值來表征同一高度處井壁所受動態應力值的大小。此處的相對誤差率是指理論計算、數值模擬、相似試驗三者所得貯礦段井壁動態應力兩兩間差值的極大值與相似試驗所得貯礦段井壁動態應力值之比。

分析表7可知：理論計算、數值模擬、相似試驗所得貯礦段井壁動態應力，在放礦口以上（5.0 m，15.0 m）范圍內，均超過了226 kPa，放礦口以上（15.0 m，30.0 m）范圍內，均不足208 kPa；三者所得井壁動態應力的最大相對誤差率在19%以內，驗證了理論計算公式的合理性。

為了更直觀地反映貯礦段井壁動態應力分布特征同井壁磨損分區的對應關系，將數值模擬與相似試驗所得貯礦段左壁與右壁動態應力分布特征（圖5（a））同文獻［17］中貯礦段井壁磨損分區范圍（圖5（b））進行對比，其中，同側井壁同一高度處的井壁動態應力取數值模擬與相似試驗中的極大值，對比結果如圖5所示。文獻［17］中，利用自主構建的溜井放礦相似試驗平臺，測定并還原金山店鐵礦主溜井貯礦段井壁重磨損區距放礦口的距離為7.0～14.28 m，距放礦口14.28 m以上區域為輕磨損區。

分析圖5可知，井壁動態應力分布云圖（a）中，放礦漏斗放礦口以上（5.0 m，15.0 m）范圍內，井壁動態應力較大，放礦口以上（15.0 m，30.0 m）范圍內，井壁動態應力較小；數值模擬和相似試驗中，盡管放礦漏斗以上溜井貯礦段左壁與右壁動態應力之間存在差異，但兩者間的差值很小，兩者間的最大差值相對于最大動態應力而言差值不足12.8%（相似試驗），對整個溜井貯礦段井壁動態應力分布特征的研究影響較小，理論計算時將圓口單側斜漏斗結構對放礦漏斗以上井壁動態應力分布的影響忽略是可行的。井壁磨損分區范圍圖（b）中，放礦口以上7.0～14.28 m范圍內為重磨損區，距放礦口14.28 m以上為輕磨損區。本研究所得溜井貯礦段井壁動態應力分布特征，同文獻［17］中采用相似試驗所得溜井貯礦段井壁磨損分區結果能夠相互對應，井壁動態應力越大則井壁磨損程度也越重。

6 結論

本研究針對溜井放礦過程中貯礦段井壁頻繁發生的磨損破壞問題，以金山店鐵礦主溜井為工程背景，推導了貯礦段井壁動態應力的理論計算公式，并通過數值模擬、相似試驗對理論計算結果進行了驗證。綜合對比理論計算、數值模擬、相似試驗所得井壁動態應力分布特征同井壁磨損分區的對應關系，驗證了研究結果的合理性，從力學角度解釋了貯礦段各處井壁磨損程度差異的原因。

（1）三者所得貯礦段井壁動態應力最大相對誤差率在19%以內，井壁動態應力分布特征同井壁磨損分區結果能夠相互印證，驗證了理論計算公式的合理性。

（2）三者所得貯礦段井壁動態應力與其距放礦口的距離呈負相關；三者所得井壁動態應力的均值，在放礦口以上（5.0 m，15.0 m］范圍內均超過了228 kPa，在（15.0 m，30.0 m］范圍內均不足204 kPa，分別對應于相似試驗中井壁的重磨損及輕磨損區；井壁動態應力越大的部位，井壁磨損程度也越重。