基于改進的小波變換電力系統諧波分析

康家玉 曹志威 王旭 劉甲琛

摘 要： 小波變換（WT）具有可變的時?頻窗口，能夠聚焦信號的任意細節，適用于非穩態及瞬變信號的分析和處理，但因存在小波混疊現象，導致其分析的精度低、魯棒性差。針對db20小波消失矩階數大的特性和良好的頻帶劃分效果，同時為滿足電力系統諧波有效分析的要求，提出基于db20小波變換抗混疊的諧波分析方法。該方法首先將信號按頻帶分解成子頻帶信號，再利用連續小波變換分析子頻帶信號，獲取諧波信息。經Matlab仿真表明，所提方法能夠有效地分析電力系統諧波信號。

關鍵詞： 小波變換； db20小波； 小波混疊； 子頻帶信號； 抗混疊； 電力系統諧波

中圖分類號： TN915?34； TM711 文獻標識碼： A 文章編號： 1004?373X（2018）19?0049?05

Abstract： Wavelet transform （WT） with variable time?frequency window can focus on any details of the signal and is suitable for the research and analysis on non?steady state and transient signals， but the presence of wavelet aliasing phenomenon leads to the low accuracy and poor robustness for harmonic analysis. Since the db20 wavelet has the characteristics of high?order vanishing moments and perfect effect for frequency band division， the harmonic analysis method based on db20 anti?aliasing wavelet transform is proposed to meet the requirement of power system for effective harmonic analysis. The method is used to decompose the signal into sub?band signals according to the frequency bands， and then the continuous wavelet transform is used to analyze the sub?band signals to acquire the harmonic information. The simulation results of Matlab show that the proposed method can analyze the harmonic signal of power system effectively.

Keywords： wavelet transform； db20 wavelet； wavelet aliasing； sub?band signal； anti?aliasing； power system harmonic

0 引 言

隨著非線性負荷的大量使用，電力系統中的諧波危害日益嚴重，對供電質量造成嚴重污染，也降低了電力系統的可靠性和穩定性。因此，諧波治理具有明顯的社會經濟效益[1?4]。

諧波分析是諧波治理的基礎，準確分析各次諧波并獲取諧波信息能夠為諧波治理提供理論依據。傳統諧波信號經典的分析方法是短時傅里葉變換（Short?time Fourier Transform，STFT）。STFT算法通過給信號加窗再分段做傅里葉變換，雖能進行信號的時頻分析，但存在時頻窗固定的問題，無法達到非穩態信號變化的頻率需求。傅里葉變換作為全局變換，難以表征信號的局部信息；小波變換（Wavelet Transform，WT）作為時頻局部化分析方法，具有頻域帶通特性及對信號的自適應性、對瞬態信號的敏感性，成為非穩態瞬變信號分析與研究的重要工具[5?6]。文獻[7]指出Daubechis系列小波具備電網諧波分析要求的良好特性，廣泛應用于電力系統諧波分析。文獻[8?10]指出db20小波具有消失矩階數較大的特性和良好的頻帶劃分效果，適合電力系統諧波信號的研究。但小波函數在信號分析中存在小波混疊，達不到信號分析精度和魯棒性的要求，阻礙了小波變換工程應用的進一步發展。

本文根據現有措施能有效地抑制小波混疊，同時結合db20小波在電力系統信號分析中的優勢，提出基于db20小波變換抗混疊的諧波分析方法。經Matlab仿真證實，該方法能有效地分析電力系統諧波信號。

1 小波變換

小波變換具有靈活可變的時?頻窗口，不僅能提取非穩態、突變和高頻衰減奇異信號的頻率成分，而且能定位信號在時域上的具體位置，能較好地獲得信號的局部特征，滿足對電力系統諧波信號分析、研究精度的要求。

2 小波混疊的原因分析及混疊補償算法

小波混疊的問題由來已久，文獻[11?13]從物理本質層面解釋了混疊現象產生的原因，認為由Heisenberg不確定性原理和Gabor理論，在信號分析時小波函數保持恒Q性質同時滿足Heisenberg不確定性原理，但尺度參數的變化將必然導致不能滿足Gabor理論，則其對應的頻帶出現混疊。此外，在小波變換中，大部分小波函數不能對信號嚴格分頻而造成小波混疊，必須重構頻帶劃分良好的小波函數。從小波濾波器的角度研究發現，小波混疊的原因來自于小波分解的隔點抽樣和重構的隔點插零的不一致，導致子頻帶重構時產生頻率混疊[14?16]。

小波濾波器是非理想濾波器，在小波分解過程中隔點采樣和在重構過程中隔點插零，兩次的頻率折疊無法實現相互抵消，處理電力系統信號時，這種混疊會影響重構后的信號，進而對諧波檢測與分析產生較大的阻礙。為消除或減弱混疊，采取兩個措施：

1） 選取db20小波。dbN系列小波隨階次[N]的增大，小波曲線越平滑，頻帶劃分效果越好，但同時會使計算量增大，綜合考慮采用db20小波。當采樣頻率為800 Hz時，db20小波的頻域特性如圖1所示。圖中，h，H為低通濾波器，g，G為高通濾波器。可以看出，圖中曲線較為平滑，低通和帶通部分出現重疊，但重疊的頻帶范圍相對較小。

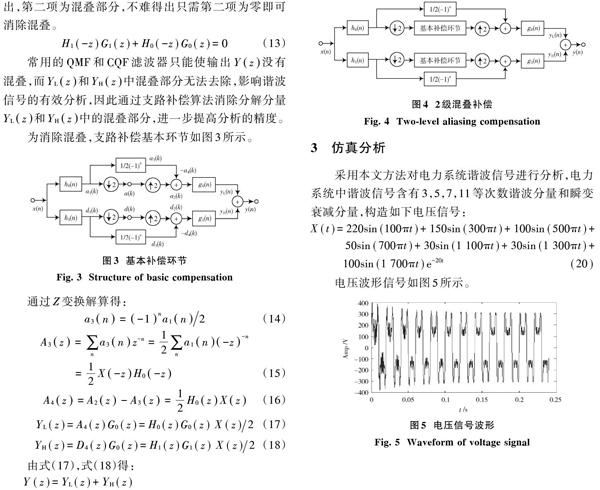
2） 通過在小波濾波器環節增加輔助支路進行補償。圖2是算法網絡結構環節。其中[h0（n），h1（n）]為小波分解的低、高通濾波器；[g0（n），g1（n）]為小波重構的低、高通濾波器；符號↓2為向下抽樣；符號↑2為向上抽樣；[x（n）]為初始信號；[y（n）]為重構信號；[a（n），d（n）]分別為小波分解的近似及細節系數；[yL（n），yH（n）]分別為小波重構的近似及細節信號，對網絡結構采用[z]變換進行分析。

由式（19）可以看出，在小波濾波器環節添加輔助支路進行補償后得到希望輸出部分，即輸出無混疊；但研究過程中發現逼近和細節部分[a（k），d（k）]依然存在混疊，借助上述原理，提出雙通道2級混疊補償方案，由圖4基本補償環節消除[a（k），d（k）]中的混疊，由此實現[a（k），][d（k），yL（n），yH（n）]均無混疊，且運算量較少。

現代電力系統出現異常狀況時，信號中含有突變、短時沖擊、高頻諧振等諧波成分，FFT因其丟失時間信息，無法定位諧波信號的發生時刻；WT具有可變的時?頻窗口，適合分析不平穩信號。改進的WT分析方法通過db20小波變換將信號按頻帶分解成低頻和高頻部分，提取小波系數，從而得到信號的突變頻率和信號在時域的具體位置并重構這些奇異分量。db20小波良好的頻帶劃分效果及小波混疊補償算法不僅使輸出無混疊，同時消除了分解分量中存在的混疊部分，提高了WT分析的容錯性和精度。

根據國標規定，電力系統要求能夠分析到60次諧波，因此允許諧波頻率要求達到3 kHz。由采樣定理得，最小的采樣頻率為6 kHz，為方便實際分析，取采樣頻率為6.4 kHz。電力系統中存在低次諧波，合理細分頻帶對諧波分析尤其重要，同時為保證諧波分析的準確度和有效性，本文選用的分解層數為5層。分析小波選用頻帶劃分效果較好的db20小波。

圖6為未采用抗混疊的小波分解系數圖，由圖6直觀看出，各頻率幅值變化趨勢不同且幅值包絡沒有上沖。經db20小波變換，低頻系數a5和高頻系數d5頻帶范圍分別為0～100 Hz，100～200 Hz。圖7為采用抗混疊的小波分解系數圖，由圖7a）的d5、圖7b）的a5小波重構波形中得出，采取抗混疊，小波變換能夠準確提取出基波分量和3次低頻諧波分量，且圖7a）的d1幅值幾乎為0，沒有能量泄露。未采用抗混疊的頻譜圖如圖8所示，由圖8a）可以看出直接進行db20離散小波變換分析，不僅存在混疊，而且子頻帶中出現了未知的頻率成分，這其實是小波調制現象。采用抗混疊的頻譜圖如圖9所示，圖9a）提取的信號已消除混疊且沒有頻譜泄露，信號較純，但仍存在上述小波調制現象；圖9b）的a1頻譜圖中不僅包含基波，3，5，7，11，13次諧波，而且還含有17次衰減信號，即把原信號中的諧波全部分離，驗證了db20小波具有良好的頻帶劃分效果。

由圖7a）中d2（頻帶范圍：800～1 600 Hz）波形圖可以得出，本文方法分離出了瞬態衰減信號且波形按指數衰減，起始最大幅值、時刻與理論瞬態衰減諧波分量相符。

經分析頻譜圖可得電壓信號基波、各次諧波FFT幅值與理論值對比見表1。由表1可清晰地看出，本文的分析方法得到的結果幅值與理論值相近，能夠有效地分析諧波信號。

4 結 論

本文結合db20小波在電力系統信號分析中的優勢和小波混疊的補償算法，提出基于db20小波變換抗混疊的諧波分析方法。通過db20小波變換，將信號分解成低頻和高頻部分，可有效地獲取信號突變的時刻及幅值信息。現代電力系統出現故障時，信號中含有突變和短時沖擊等諧波成分，利用模極大值理論對這些成分進行離散小波變換分析，捕捉信號的突變頻率及確定信號在時域的具體位置，能準確分析大部分非穩態諧波。本文方法也存在不完善，文中子頻帶信號出現了未知的頻率成分，是用連續小波變換分析多頻諧波信號而產生的小波調制現象，抑制和處理小波調制混頻是本文分析方法鞭長莫及的地方，這也是筆者以后的研究方向。

參考文獻

[1] 何韜，梁棟，李瑤，等.小波變換在電力諧波分析中的應用[J].計算機技術與發展，2007，17（1）：229?232.

HE Tao， LIANG Dong， LI Yao， et al. Application of wavelet transform in harmonic analysis of power [J]. Computer technology and development， 2007， 17（1）： 229?232.

[2] 曾瑞江，楊震斌，柳慧超.基于小波變換的電力系統諧波檢測方法研究[J].電力系統保護與控制，2012，40（15）：35?39.

ZENG Ruijiang， YANG Zhenbin， LIU Huichao. A method of power system harmonic detection based on wavelet transform [J]. Power system protection and control， 2012， 40（15）： 35?39.

[3] 陳方超，汝曉鵬，申江江.小波分析在電力系統諧波處理中的應用[J].電子設計工程，2015（3）：100?103.

CHEN Fangchao， RU Xiaopeng， SHEN Jiangjiang. Wavelet analysis in power system harmonic processing [J]. Electronic design engineering， 2015（3）： 100?103.

[4] 張旭東.基于小波分析的地方電網諧波檢測方法研究[D].西安：西安科技大學，2014.

ZHANG Xudong. Research on local harmonic detection method based on wavelet transform [D]. Xian： Xian University of Science and Technology， 2014.

[5] 亓學廣.基于FFT和小波變換的電力系統諧波檢測方法研究[D].青島：山東科技大學，2007.

QI Xueguang. Study on harmonic detection methods in power system based on FFT and wavelet transform [D]. Qingdao： Shandong University of Science and Technology， 2007.

[6] 吉艷平.基于小波變換的電力諧波檢測方法的研究[D].長沙：中南大學，2007.

JI Yanping. A method of power system harmonic detection based on wavelet transform [D]. Changsha： Central South University， 2007.

[7] 朱翔，解大，高強，等.db8小波在電力系統諧波分析中的應用[J].電力科學與技術學報，2011，26（2）：67?71.

ZHU Xiang， XIE Da， GAO Qiang， et al. On the application of analyzing power system harmonic using db8 [J]. Journal of electric power science and technology， 2011， 26（2）： 67?71.

[8] 朱翔，解大，高強，等.基于FFT和db20小波變換的電力系統諧波聯合分析策略[J].電力系統保護與控制，2012，40（12）：62?65.

ZHU Xiang， XIE Da， GAO Qiang， et al. Analyzing strategy for power system harmonics on FFT and using db20 [J]. Power system protection and control， 2012， 40（12）： 62?65.

[9] 何智龍，蘇娟，覃芳.db20和db3小波變換的電力系統諧波聯合分析[J].智能電網，2015，3（2）：129?132.

HE Zhilong， SU Juan， QIN Fang. Conjoint analysis for power system harmonics based on db20 and db3 wavelet transform [J]. Smart grid， 2015， 3（2）： 129?132.

[10] 趙景波，唐勇偉，張磊.基于改進小波變換的故障電弧檢測方法的研究[J].電機與控制學報，2016，20（2）：90?97.

ZHAO Jingbo， TANG Yongwei， ZHANG Lei. Improved wavelet transform algorithm of anti spectrum aliasing based on adding odd extraction before a node [J]. Electric machines and control， 2016， 20（2）： 90?97.

[11] 杜天軍，陳光，謝永樂，等.基于頻域內插抗混疊Shannon小波包變換的諧波檢測方法[J].電網技術，2005，29（11）：14?19.

DU Tianjun， CHEN Guang， XIE Yongle， et al. Harmonic detection based on frequency domain interpolation anti?aliasing Shannon wavelet packet transform [J]. Power system technology， 2005， 29（11）： 14?19.

[12] 龍軍，劉俊杰，王冠南，等.基于小波變換的電力系統諧波檢測抗混疊問題研究[J].電氣開關，2012，50（5）：22?25.

LONG Jun， LIU Junjie， WANG Guannan， et al. Research on anti?aliasing problem for power system harmonic detection based on wavelet transform [J]. Electric switchgear， 2012， 50（5）： 22?25.

[13] 杜天軍.基于抗混疊小波理論的電力系統諧波檢測與抑制研究[D].成都：電子科技大學，2006.

DU Tianjun. Study on harmonic detection & suppression in power system based on anti?aliasing wavelet theories [D]. Chengdu： University of Electronic Science and Technology of China， 2006.

[14] 杜天軍，陳光，雷勇.基于混疊補償小波變換的電力系統諧波檢測方法[J].中國電機工程學報，2005，25（3）：54?59.

DU Tianjun， CHEN Guang， LEI Yong. A novel method for power system harmonic detection based on wavelet transform with aliasing compensation [J]. Proceedings of the CSEE， 2005， 25（3）： 54?59.

[15] 杜天軍，陳光，謝永樂.利用內插優化技術解決諧波檢測小波混疊[J].電力系統自動化，2005，29（5）：62?68.

DU Tianjun， CHEN Guang， XIE Yongle. Using interpolation optimization technology to solve harmonic detection and wavelet aliasing [J]. Automation of electric power systems， 2005， 29（5）： 62?68.

[16] 陳長升，黃險峰.基于小波變換抗混疊諧波檢測的一種新方法[J].電力系統保護與控制，2008，36（23）：23?26.

CHEN Changsheng， HUANG Xianfeng. A novel method for anti?aliasing harmonic detection based on wavelet transform [J]. Power system protection and control， 2008， 36（23）： 23?26.