基于MR框架的不確定時間序列相似性計算方法
李成為,王 嶼,鄭迪威
(南京航空航天大學 計算機科學與技術學院,江蘇 南京 211106)
0 引 言
不確定時間序列(uncertain time series)是按照時間戳先后順序排列的記錄值的序列,在每個時間戳的序列值都是未知的或者不可預料的。不確定時間序列數據廣泛應用于定位服務[1]、醫療數據分析[2]、時序數據庫[3]、無線傳感器網絡[4]等等。不確定性的產生是由于數據采集和環境方面的誤差[5]、使用了預測技術[6-7],以及對于測量屬性的多次讀取數據[8]等因素。
在不確定時間序列數據處理的諸多任務和問題中,不確定時間序列相似性計算是其很重要的一個部分[9]。對于不確定時間序列相似性計算方法,主要從兩個方向進行研究:一個是參考最初為確定性時間序列數據提出的相似性計算算法來進行改造[10-11];一個是根據不確定時間序列的特性,融合傳統的確定性時間序列相似性算法思想,提出專門適用于不確定時間序列的相似性算法[6-7,12-14]。文中主要對第二個方向進行研究。
在傳統的確定性時間序列相似性計算方法中,DTW由于不要求兩個序列等長,并且兩個序列求差值的點可以一對多或多對一,廣泛用于計算各種情況的時間序列相似性。文獻[8]針對經典DTW算法具有較高計算時間和空間損耗的問題,提出解決流檢測問題的ShortestDTW算法;文獻[14]通過多次在一些超平面上的投影來組織序列,提出了FastDTW算法,但該算法需要預先知道不同對象之間的距離,屬于一種粗獷的過濾方式,會帶來許多不相似的噪音;文獻[15]基于DTW原理提出了TD算法,對時間跨度較大且體現一個連續、完整過程的時間序列數和時間跨度較小、體現狀態點的時間序列數據具有一定的計算效果;文獻[16]提出一種將特征提取和降維進行融合的PLA-SDTW算法,可解決高維時間復雜度的問題。
針對時間序列數據具有較大數據量的特點[17],近年來已有研究工作嘗試使用MapReduce計算框架[18]計算時間序列的相似性。文中基于傳統DTW算法,通過融入MR計算框架,提出一種不確定時間序列的相似性計算算法。該算法在不確定時間序列計算規模大時,并行計算每個子矩陣的動態時間規整距離,在獲得與原DTW同等的匹配效果的同時,可使計算時間復雜度大為縮小。
1 基礎知識
1.1 時間序列相似性計算
給定一個收集好的時間序列C={S1,S2,…,SN},其中N表示時間序列的數量,查詢函數定義為:RQ(Q,C,ε)={S|S∈C|distance(Q,S)≤ε},其中ε是使用者提供的距離閾值。
(1)DTW距離。
給定兩個時間序列Q和C,它們的長度分別為n和m,將這兩個時間序列記為:Q=
其中,φ表示空時間序列;First(Q)表示時間序列Q的第一個元素;Rest(Q)表示時間序列Q除第一個元素外其他元素組成的子序列;dist2(x,y)為兩點x和y的距離,通常采用歐氏距離進行計算。DTW的計算復雜度為O(nm),計算代價較高,所以有研究人員對距離進行了變形處理。
(2)FastDTW距離。
先將兩個時間序列粗粒度化,在遞歸到最底層后尋找最短DTW路徑,然后每次細粒度擴展r個單位(r為半徑),即將路徑及其周圍的點逐步細粒度化,并再次尋找最短DTW路徑,最終求出原始序列間的DTW距離。
FastDTW的細粒度化計算過程如圖1所示。
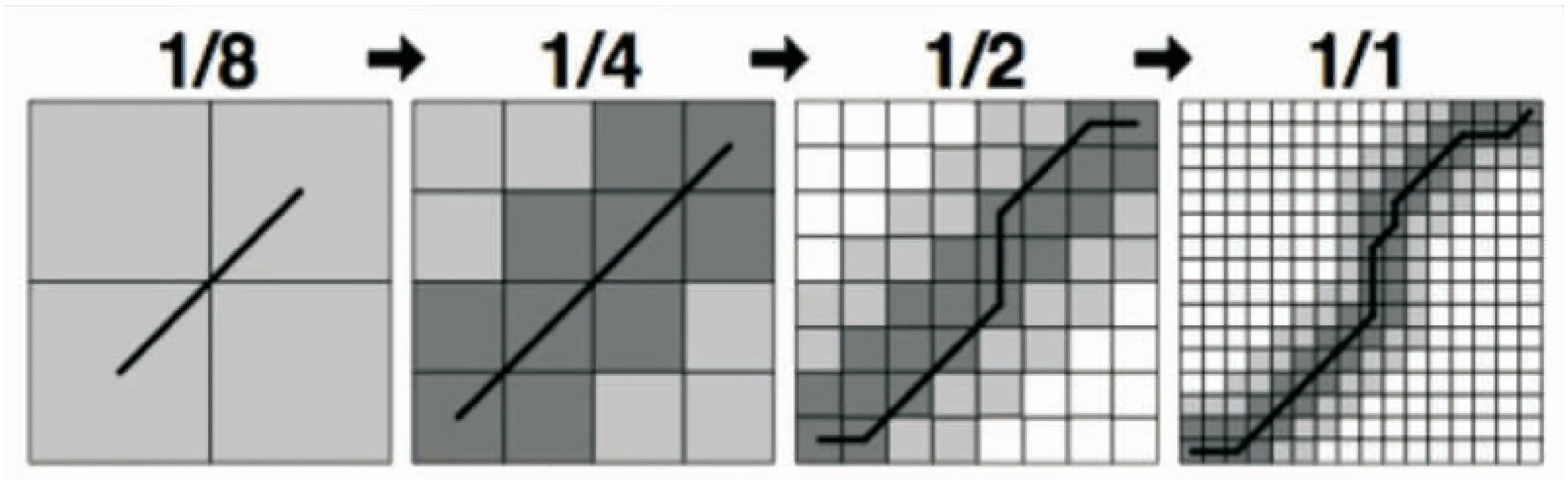
圖1 FastDTW的細粒度化計算過程
第一幅圖表示在遞歸最底層階段執行DTW算法。第二幅圖表示在遞歸返回階段,將第一幅圖求得的路徑經過的方格進行細分,并且向左右,上下,以及左上右下的斜對角方向擴展r個單位,重新執行DTW算法得到的新路徑。以此類推,直到最后求得最終的路徑。
1.2 不確定時間序列及其期望距離
不確定時間序列的每個元素x都可以表示為x=r(x)+ε(x),其中r(x)表示該元素的真實值,ε(x)表示該元素的誤差,是服從某一連續型分布函數或某離散型分布的隨機變量。不確定時間序列T定義為一系列隨機值的集合T=
期望距離[19]可以用來計算兩個不確定時間序列數據之間的距離,該算法是用所有可能出現的計算結果的均值加上誤差值來代表這兩個不確定時間序列之間的距離。期望距離的具體定義如下:兩個時間序列X,Y(其中至少有一個是不確定時間序列)的概率分布為f(x)、f(y),則它們的期望距離為:
其中,pointsdis(x,y)可以用‖x-y‖2表示,即x2+y2-2|xy|,可以推導出:
上述公式即表明了期望距離可以用時間序列中各個時間點之間的距離的期望和方差來表示,由此可以大大減少不確定時間序列之間點與點之間距離的計算量。
2 MR-FastDTW算法
FastDTW算法通過粗細粒度化的變化,在計算路徑時,首先計算遞歸最底層的路徑,并在返回階段,圍繞著上一階段得出的路徑拓展相應范圍的計算矩陣,減少DTW暴力求解所造成的無用計算帶來的損耗。
算法1描述了FastDTW的計算過程:
算法1:FastDTW算法
Input:長度分別為|X|和|Y|的兩段時間序列X和Y;
閾值Radius//最粗分辨率的最小值
Output:時間序列X和Y之間的最小DTW距離;X與Y之間的規整路徑
1.Integer minTSsize=radius+2
2.IF(|X|≤minTSsize OR |Y|≤minTSsize)
3.RETURN DTW(X,Y)
4.ELSE
5.TimeSeries shrunkX=X.reduceByHalf()
6.TimeSeries shrunkY=Y.reduceByHalf()
7.WarpPath lowResPath=FastDTW(shrunkX, shrunkY,radius)
8.SearchWindow window=Exp[andeResWindow(lowResPath,X,Y,radius)]
9.RETURN DTW(X,Y,window)
針對FastDTW計算方法在遞歸返回階段執行到一定程度后,文中采用MR計算框架簡化相似性計算,提出了MR-FastDTW算法,以提升運行速度。
對于一個給定的不確定時間序列,在FastDTW算法執到第1步和第12步時,MR-FastDTW算法采用了期望距離來執行不確定性數據的相似性計算。在執行MR計算框架時,對于遞歸到一定程度后即第12步,對矩陣進行分塊處理,分塊好的矩陣進行Map處理,產生相應的
1.輸入采集到的序列A、待檢測的確定時間序列B。
2:執行FastDTW算法,DTW計算過程使用期望距離來計算。當粗粒度進行到第n(n>3)次細粒度化時,把細粒度化好的矩陣放入MR計算框架中執行計算。
3:執行MR計算。
(1)由于DTW的計算矩陣是n*m矩陣,將序列X劃分為長度分別為[m/p]的p個子序列X0,X1,…,Xp-1,將序列Y劃分為長度分別為[n/q]的q個子序列Y0,Y1,…,Yq-1。于是就構造了p*q個子矩陣Mf*g,f[1,p],g[1,q]。每個子矩陣的規模為[m*n]/[p*q]。
(2)每個子矩陣求的路徑作為key值,編號作為value值進行排序。
(3)排序過后的值傳入Reduce部分,進行路徑匯總篩選,并規約在一起得出總的動態規約路徑。
算法2描述了MR-DTW的計算過程:
算法2:MR-DTW算法
Input:時間序列X,Y,規約窗口window,p,q
Output:MR-DTW(X,Y,window)//需要加上window參數
1.INTEGERn/q,m/p
2.DTW(n2,m2)
3.MAP://MAP階段
4.E((1,2,…,n/q),m/p)→HDFS //D1*1最后一行的值
5.E(n/q,(1,2,…,m/p))→HDFS→HDFS//D1*1最后一列
6.HDFS[E((1,2,…,n/q),m/p)]→Matrix((n/q,n/q+1,…,n/q*2),m/p)
7.D(n/q*2,m/p)
8.//讀取HDFS中的D1*1最后一行,存入D2*1的第0行
9.HDFS[E(n/q,(1,2,…,m/p))]→Matrix(n/q,(m/p,m/p+1,…,m/p*2))
10.D(n/q*2,m/p*2)
11.//讀取HDFS中的D1*1最后一列 ,存入D1*2的第0列
12.E(n/q,(m/p,m/p+1,…,m/p*2))→HDFS
13.E((n/q,n/q+1,…,n/q*2),m/p)→HDFS
14.//將第D1*2的最后一列和D1*2的最后一行存到HDFS
15.//…并行計算子矩陣,中間重復步驟
16.HDFS[E((n*(q-2)/q,n*(q-2)/q+1,n(q-1)/q),m)]→Matrix((n(q-1)/q,n(q-1)/q+1,…,n),m)
17.HDFS[E(n,(m*(p-2)/p,m*(p-2)/p+1,…,m(p-1)/p))]→Matrix(n,(m*(p-1)/p,m*(p-1)/p+1,…,m))
18.D(n,m)
19.//獲取子矩陣D(f-1)*g的最后一行以及矩陣Df*(g-1)的最后一列,存入到Df*g的第0行第0列,計算Df*g
20. SORT: //SORT階段
21.Sort(D(n/q,m/p),…,D(n,m))//對p*q個矩陣的值排序
22.REDUCE://REDUCE階段
23.Combime(key) according to the sort result
24.//根據sort結果,篩選鏈接每個小矩陣的值
25.Return DTW(n,m)
把MP-DTW算法與FastDTW算法相結合,得到了基于MR計算框架的MR-FastDTW算法。算法3描述了MR-FastDTW的計算過程:
算法3:MR-FastDTW算法
Input:長度分別為|X|和|Y|的兩段不確定時間序列X和Y,FastDTW擴展半徑r,起始執行并行算法閾值num
Output:MR-FastDTW動態彎曲矩陣距離
1.Integer minTSsize=radius+2
2.IF(|X|≤minTSsize OR |Y|≤minTSsize)
3.RETURN DTW(X,Y)
4.ELSE
5.TimeSeries shrunkX=X.reduceByHalf()
6.TimeSeries shrunkY=Y.reduceByHalf()
7.WarpPath lowResPath=FastDTW(shrunkX,shrunkY,radius)
8.SearchWindow window=Exp[andeResWindow(lowResPath,X,Y,radius)]
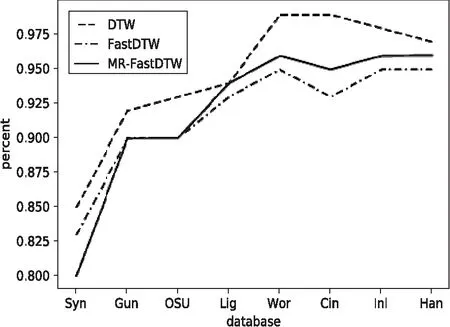
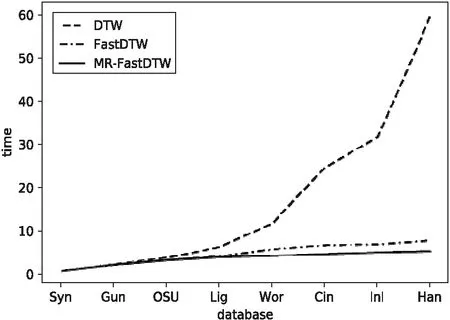
9.IF NUM 10.RETURN DTW(X,Y,window) 11.ELSE 12.RETURN MR-DTW(X,Y,window) 從UCR數據集中隨機抽取8組數據作為實驗測試數據集。8組數據的具體構成見表1。 表1 由UCR數據集構建的不確定時間序列 實驗采用4臺計算機通過路由器組建Hadoop集群,每臺計算機的內存為4 GB,處理器為Intel i5-6500,操作系統為Win7。一臺作為主節點,三臺作為數據節點。使用表1中的數據集人工合成不確定時間序列,對MR-FastDTW算法與傳統的DTW算法和FastDTW算法進行比較。 (1)精確度對比。 精確度是對比不同算法之間準確性的標準,即不同算法檢測的結果與實際不確定時間序列的結果相比較的準確程度。由于不確定數據存在誤差,所以對每組實驗數據測十次,并取均值。再用不同的算法單次讀取該數據,并與均值進行比較。DTW算法未對數據進行任何限制處理,所以得到的結果精確度最高;FastDTW算法采用了粒度化的方法對數據集進行了限制處理,精確度略有下降,但仍有較高的準確度;MR-FastDTW算法的精確度與FastDTW算法的精確度基本一致,也表現出較高的準確度。精確度比較如圖2所示。 圖2 相似性算法的精確度比較 (2)時間復雜度對比。 時間復雜度主要是不同算法執行同組數據所消耗的時間。時間復雜度的比較如圖3所示。 圖3 相似性算法的時間復雜度比較 從圖3可以看出,當數據量很小時,三種算法沒有太大的差異。當參與計算的數據量逐步增加時,DTW算法其時間消耗隨數據規模的增大開始非線性增長,FastDTW算法和MR-FastDTW算法的時間消耗表現平穩。當數據量規模超過900時,DTW算法時間消耗會急劇增長,FastDTW算法由于是串行計算,時間消耗有所增大,而MR-FastDTW算法由于是并行處理,時間消耗最小。 提出了基于MR計算框架的MR-FastDTW算法,解決了FastDTW在遞歸返回段執行到一定程度后計算量大的問題,在提高計算速度的同時,提高了計算準確性。 需要指出的是,目前MR-FastDTW算法在執行過程中需要使用閾值,它控制著遞歸返回段進行到何種程度時再進行MapReduce計算,因此閾值是MR-FastDTW算法實現的一個關鍵點。但是,閾值的取值目前還沒有一個嚴格的范圍標準,當前只是大概取程序在遞歸返回階段執行到三分之一時刻的值,這只是經驗值,缺乏嚴格的論證和理論依據。此外,該算法在執行矩陣拆分以及合并計算值時,操作還稍顯繁瑣。所有這些都將是未來工作中需要改進的地方。3 實驗驗證
3.1 測試數據集的選擇
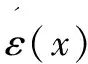
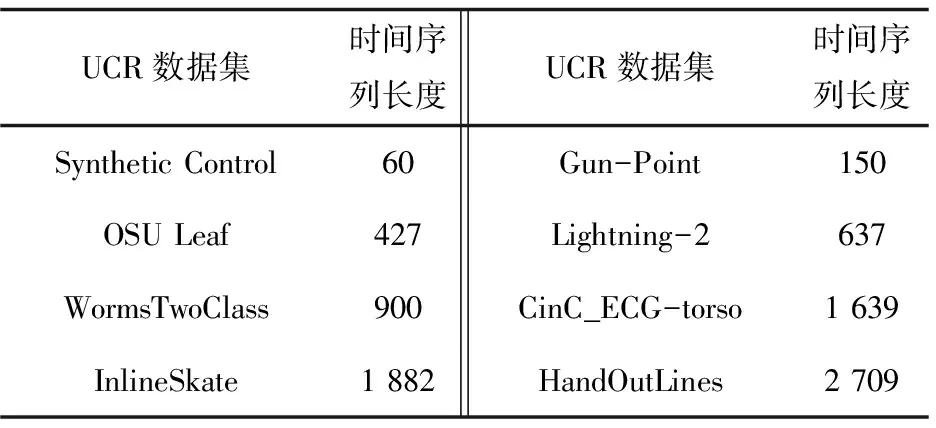
3.2 算法精確度和復雜度的比較
4 結束語

