柔性制造系統的部分可觀時間Petri網故障診斷

張治國，劉久富，鄭 銳

(南京航空航天大學 自動化學院，江蘇 南京 210016)

0 引 言

柔性制造系統(flexible manufacturing system，FMS)通常由多個單元構成，各單元相互配合完成復雜加工任務。成熟的柔性制造系統動態行為更加復雜，可在24小時無人操作下智能生產，極大減少工人工作量，滿足企業對市場需求的應變[1-3]。柔性制造系統在制造業的優勢越來越明顯，但實際生產過程中，也存在制造復雜，運行模式多樣化等導致故障頻繁，故障樣本難以獲取，關鍵設備無法及時檢測運行狀況等問題[4-6]。因此，對柔性制造系統的故障診斷研究勢在必行。

目前國內外很多科研機構都在開展關于柔性制造系統的故障診斷方法研究，并取得了一定成果。北京理工大學等機構在機器人可靠性分析研究時引入了故障樹的研究方法，通過故障樹定性定量的分析針對單一設備的故障診斷有了一定的理論實踐研究[7]。Kuo等從FMS運行過程的行為角度出發,使用有色Petri網建模實現對FMS的狀態監測及故障診斷[8-9]。

針對柔性制造系統，以往基于定性模型的故障方法已經取得了豐碩的成果，但主要集中在可觀節點的故障診斷，對不可觀節點的故障診斷還不夠完善。對此，文中提出一種基于部分可觀時間Petri網的故障診斷方法，把部分可觀時間Petri網[10-12]和狀態類圖(state class graph，SCG)[13-14]相結合，構建修正狀態類圖(modified state class graph，MSCG)，把復雜的并行事件轉變成求解滿足時間約束的序列集合。所有節點分為可觀節點和不可觀節點，根據各節點變遷觸發時間范圍和可觀節點觸發時間信息，結合提出的故障診斷方法，判斷系統不可觀節點是否發生故障。

1 部分可觀時間Petri網的故障檢測問題

1.1 部分可觀時間Petri網

定義1：Petri網(Petri nets，PN)定義為N=(P,T,Pre,Post)，其中P為庫所(place)集合，T為變遷(transition)集合，Pre:P×T→和Post:P×T→分別是輸入弧和輸出弧的集合，每個庫所的資源個數為M(p)。

定義2：時間Petri網(time Petri nets，TPN)定義為Nd=(N,Q),N=(P,T,Pre,Post)是Petri網的四元數組，Q:T→×(∪{∞})是系統初始狀態下變遷時間約束條件，Q(ti)=(li,ui)，li≥0,ui≥li，li和ui均為自然數。

定義3：標簽Petri網(label Petri net，LPN)定義為，L:T→L∪{ε}為每個變遷分配一個標簽L或空符號ε，分別對應可觀變遷和不可觀變遷。

1.2 故障檢測問題

(1)

定義5：給定一個時間標簽序列集合

和一個時間τ≥τl(δ0)，對應的標識集合為：

C(δ0,τ)={M∈m|M0[σ〉M,σ∈∑(δ0,τ)}

(2)

定義6：給定一個時間標簽序列集合

和一個時間τ≥tl(δ0)，對應的狀態集合為:

S(δ0,τ)={Mk,Θk|Mk∈C(δ0,τ),Θk={lki≤θki≤uki}},lki≥0，uki≥0

(3)

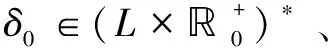
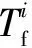
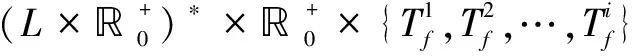
記log(σ)為去掉時刻τ的變遷序列集合。

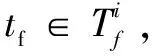
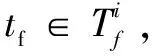
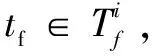
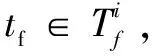
2 基于MSCG圖和時間Petri網的故障診斷方法

2.1 修正狀態類圖構建方法

在狀態類圖方法[12-13]的基礎上添加時間變量和時間約束,構建基于標簽時間Petri網的修正狀態類圖。

算法1：構建MSCT。

輸入：TPN系統

輸出：修正狀態類樹(MSCT)

1．初始化 節點C0對應標識

根節點標記B(C)=E

while 存在一個標記B(C)=E的節點do{

2．節點標識為Ck，B(C)=D

3．for ?ti∈A(Mk) do{

5．ti在標識Mk觸發，Mq=Mk+C(·,ti)

6．for ?tr∈A(Mq)do{

iftr∈A(Mk)且Mk-Pre(:,ti)≥pre(:,tr) pre(:,tr) then

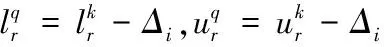
7．建立新節點Cq標識為Mq,約束集合為：

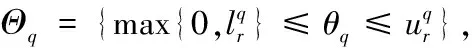
if存在和Cq相同節點 then

Cq節點標記B(C)=D

ElseCq節點標記B(C)=E}}}

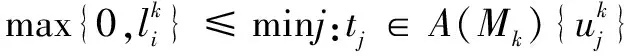
在MSCT中復制標記為B(C)=Z的節點，構建MSCG圖。

2.2 基于MSCG圖和時間Petri網的狀態估計

π=Cq0(Mq0,Θq0),ti1,L(ti1)

Cq1(Mq1,Θq1),ti2,L(ti2)

……

Cq(k-1)(Mq(k-1),Θq(k-1)),tik,L(ti(k-1))

Cqk

(4)

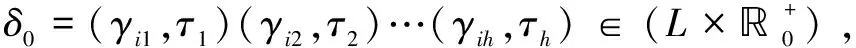
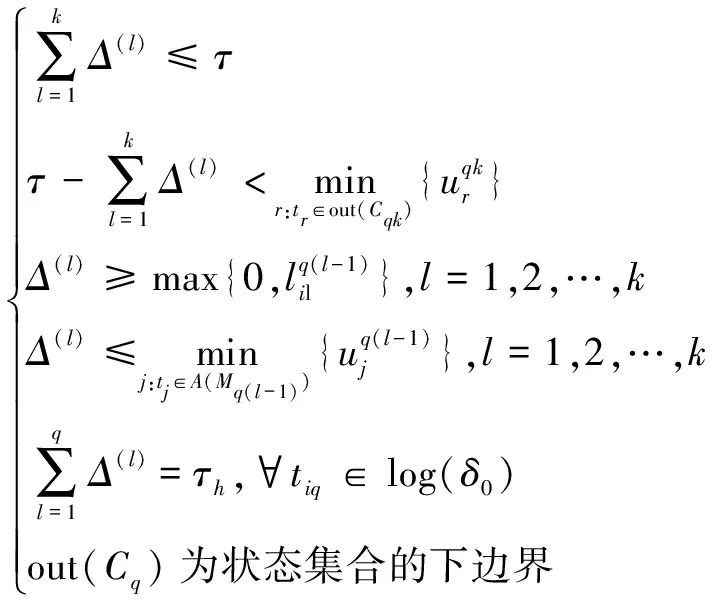
(5)

給定路徑π，定義obs(π)為其對應的可觀序列，式(5)中obs(π)=L(ti1,ti2,…,tik)。

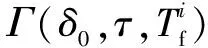
步驟16判斷系統是否發生故障。任意π∈Ⅱ，都不存在tf∈π，系統沒有故障；存在π∈Ⅱ，滿足tf∈π同時存在π'∈Ⅱ滿足tf?π'，無法判斷系統是否故障；所有π∈Ⅱ都滿足tf∈π，系統故障。

算法2：基于MSCG的狀態估計與診斷算法。

輸入：TPN系統及對應MSCG圖，TLS集合δo=(γi1,τ1)…(γih,τh)，時間τ

1.初始化:δ0=ε,S(δ0,0)=?

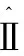
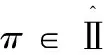
4.for 所有π∈Ⅱ路徑 do{

S(ε,0)=S(ε,0)∪{(M,Θ)}，(M,Θ)是路徑π最后節點}

5.if 給定S(ε,τ)，τ>0 then{

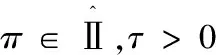
7.for所有π∈Ⅱτdo

S(ε,τ)=S(ε,τ)∪{(M,Θ′)},Θ′是根據式5得出的最后節點時間約束}

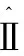
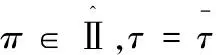
12.forπ∈Ⅱ do{

S(δ0,τ)=S(δ0,τ)∪{(M,Θ)} }

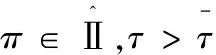
15.for所有π∈Ⅱτdo

S(δ0,τ)=S(δ0,τ)∪{(M,Θ′)} }

16.fori=1,2,…,rdo{

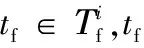
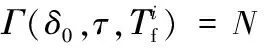
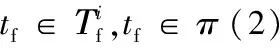
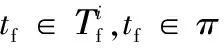
3 實例分析與驗證

某柔性制造系統(FMS)由一臺加工中心M和多臺數控機床組成，并行生產一組零件。工序設計要求工件b根據工件a在M的校刀數據進行加工。

3.1 構建柔性制造系統模型

圖1以柔性制造系統加工過程中關鍵節點為庫所，關鍵動作為變遷建立Petri網模型，模擬柔性制造系統加工過程，各庫所、變遷含義如表1、表2所示。

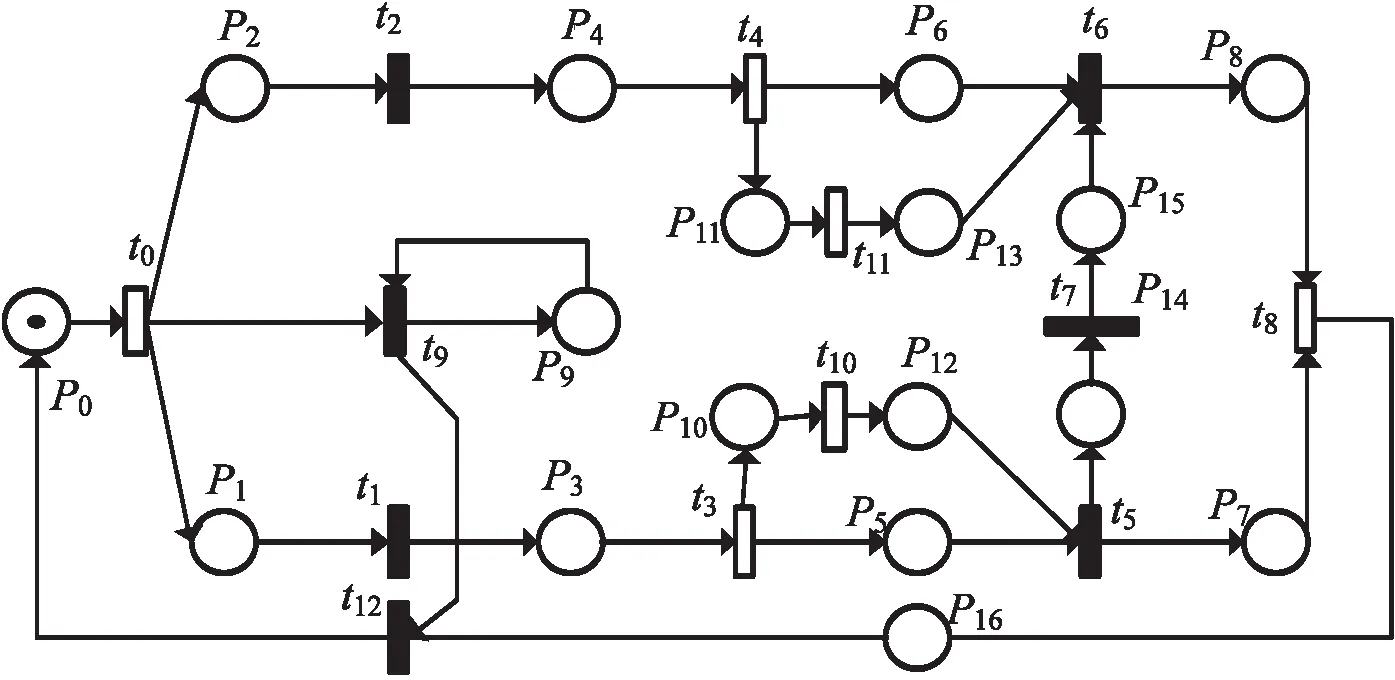
圖1 柔性制造系統Petri網模型

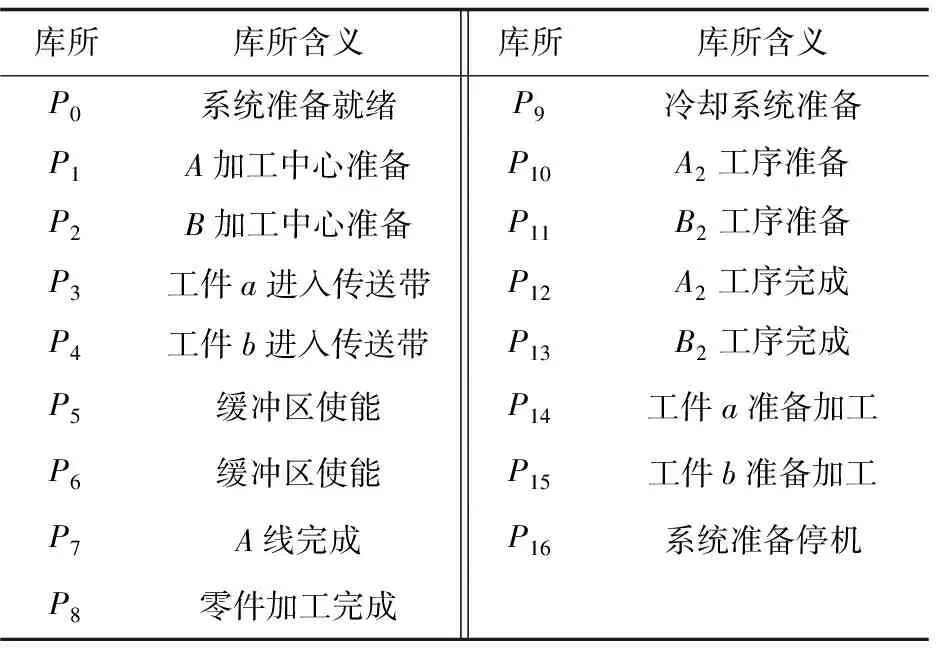
庫所庫所含義庫所庫所含義P0系統準備就緒P9冷卻系統準備P1A加工中心準備P10A2工序準備P2B加工中心準備P11B2工序準備P3工件a進入傳送帶P12A2工序完成P4工件b進入傳送帶P13B2工序完成P5緩沖區使能P14工件a準備加工P6緩沖區使能P15工件b準備加工P7A線完成P16系統準備停機P8零件加工完成

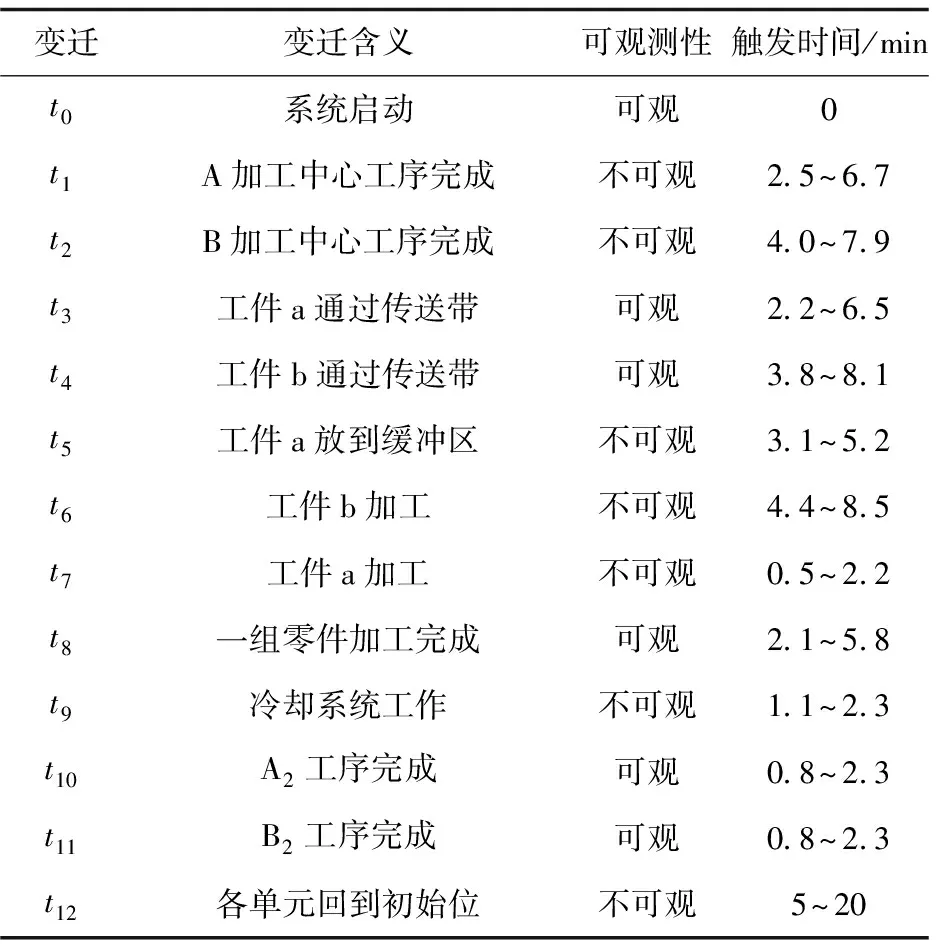
表2 圖1中各變遷物理含義、可觀測性及設計動作時間

該柔性制造系統工作流程為[15-16]：毛坯a，b分別進入A，B支路，經過數控機床相應工序變成工件a，b；工件a先進入加工中心M校準刀具加工，工件b再進入加工中心M根據工件a的校刀數據加工。最后完成一組零件的加工。

3.2 柔性制造系統故障診斷

3.2.1 構建柔性制造系統的MSCG圖

根據算法1構建MSCG圖，標識M及時間約束Θ構成每個節點的基本信息，所有可能路徑為{t0t1t2t3t4t10t11t5t7t6t8,t0t1t2t3t4t11t10t5t7t6t8,t0t1t2t3t10t4t11t5t7t6t8,t0t1t2t4t3t10t11t5t7t6t8,t0t1t2t4t3t11t10t5t7t6t8,t0t1t2t4t11t3t10t5t7t6t8}等。

圖2 節點C1C2C3對應的MSCG圖

以{t0t1t2t3t4t10t11t5t7t6t8}為例簡述修正狀態類圖構建過程，圖2是變遷t0t1觸發對應節點C1C2C3的MSCG圖。標識M0和時間約束Θ0構成初始節點C0對應的使能變遷為t0；節點C1由變遷t0在C0觸發得到，標識M1[011000000010000000]對應的使能變遷為t1,t2，且Q(t1)=[2.5,6.7]，Q(t2)=[4.0,7.9]；節點C2由變遷t1在C1觸發得到，標識M2[001100000010000000]對應的使能變遷為t2,t3，變遷t2能觸發需滿足Δ1≤min{u1,u2}，所以修正后的Q(t2)=[4.0-Δ1,7.9-Δ1]；節點C3由變遷t2在C2觸發得到，標識M3[000110000010000000]，對應的使能變遷為t3,t4，變遷t3能觸發需滿足Δ2≤min{u2,u3}，所以修正后的Q(t3)=[2.2-Δ2,6.5-Δ2]，同理構建其他節點。

3.2.2 基于MSCG圖柔性制造系統的故障診斷結果

柔性制造系統中工業機器人腰部回轉故障影響系統正常工作。文中Petri網模型中，工業機器人腰部回轉無故障情況下，工件a放到緩沖區(變遷t5)會在A2工序在3.1～5.2 min內完成，若工業機器人腰部回轉故障便會導致變遷t5完成的時間推遲到5.2～12.3 min內。圖3是根據仿真數據及文中算法進行故障診斷的結果，其中τ是采集有效數據的時間上限。

由圖3可知，在第一次實驗中，可觀序列(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)(t11,13.1)觸發后，由算法2計算所有能夠觸發的變遷序列σ，其中正常變遷4條，故障變遷0條，系統診斷結果為無故障。可觀序列(t8,24.9)觸發后，由算法2計算所有能夠觸發的變遷序列σ，其中正常變遷4條，故障變遷2條，系統診斷結果為可能故障。

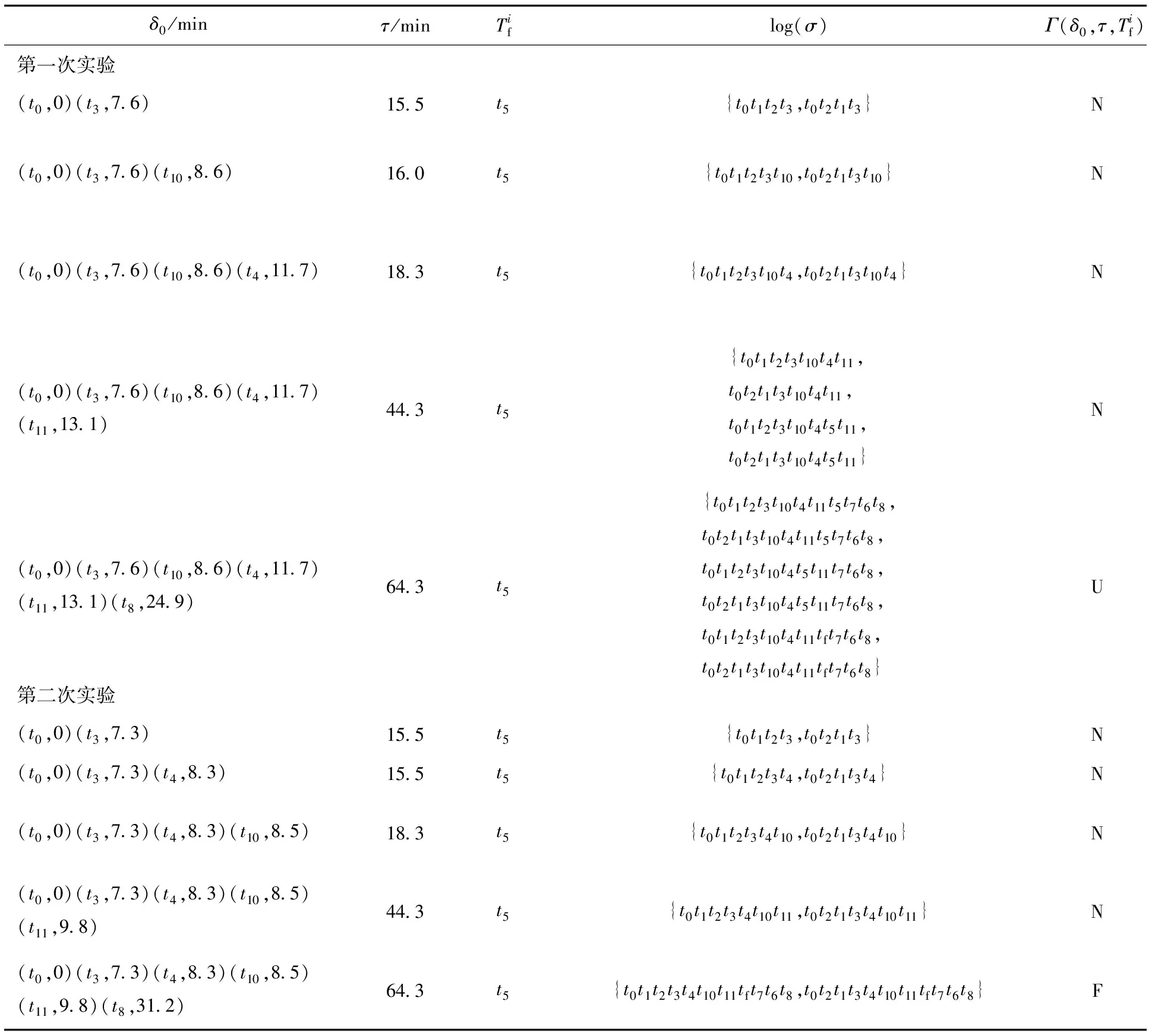
δ0/minτ/minTiflog(σ)Γ(δ0,τ,Tif)第一次實驗(t0,0)(t3,7.6)15.5t5{t0t1t2t3,t0t2t1t3}N(t0,0)(t3,7.6)(t10,8.6)16.0t5{t0t1t2t3t10,t0t2t1t3t10}N(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)18.3t5{t0t1t2t3t10t4,t0t2t1t3t10t4}N(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)(t11,13.1)44.3t5{t0t1t2t3t10t4t11,t0t2t1t3t10t4t11,t0t1t2t3t10t4t5t11,t0t2t1t3t10t4t5t11}N(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)(t11,13.1)(t8,24.9)64.3t5{t0t1t2t3t10t4t11t5t7t6t8,t0t2t1t3t10t4t11t5t7t6t8,t0t1t2t3t10t4t5t11t7t6t8,t0t2t1t3t10t4t5t11t7t6t8,t0t1t2t3t10t4t11tft7t6t8,t0t2t1t3t10t4t11tft7t6t8}U第二次實驗(t0,0)(t3,7.3)15.5t5{t0t1t2t3,t0t2t1t3}N(t0,0)(t3,7.3)(t4,8.3)15.5t5{t0t1t2t3t4,t0t2t1t3t4}N(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)18.3t5{t0t1t2t3t4t10,t0t2t1t3t4t10}N(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)(t11,9.8)44.3t5{t0t1t2t3t4t10t11,t0t2t1t3t4t10t11}N(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)(t11,9.8)(t8,31.2)64.3t5{t0t1t2t3t4t10t11tft7t6t8,t0t2t1t3t4t10t11tft7t6t8}F

圖3 柔性制造系統故障診斷結果

第二次實驗中，可觀序列(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)(t11,9.8)觸發后，由算法2計算所有能夠觸發的變遷序列σ，其中正常變遷2條，故障變遷0條，系統診斷結果為無故障。可觀序列(t8,31.2)觸發后，由算法2計算所有能夠觸發的變遷序列σ，其中正常變遷0條，故障變遷2條，系統診斷結果為故障。

4 結束語

針對Petri網模型中不可觀節點故障診斷問題，提出一種構建修正狀態類圖的故障診斷方法，由算法2計算MSCG圖中所有滿足可觀序列集合S(δ0,τ)的序列σ并診斷系統是否發生故障；建立柔性制造系統的部分可觀時間Petri網故障診斷模型，根據變遷之間觸發關系修正各自對應的時間約束，由算法1構建對應的修正狀態類圖(MSCG),再根據算法2診斷系統的故障狀態。仿真結果表明，該算法能夠滿足實際應用要求。

未來將研究標簽時間Petri網的可診斷性，系統結構和變遷數目影響構建MSCG圖的計算復雜度，當系統變遷數目過多時，該算法還需進一步改進。