波浪中船舶結構慣性力求解及實際工程應用

傅健

（海洋石油工程股份有限公司，天津 300451）

船舶在海浪中受到環境載荷的影響，作用在船舶的計算載荷主要由船舶的重力、船舶搖蕩時產生的慣性力、所受的風力及舷外水壓力四部分組成。

結構分析中各項載荷、重力和風力很容易計算和加載，但是搖擺時所引起的慣性力由于跟質量分布和船舶在波浪中的運動狀態有關，較為復雜，有必要進行研究探討[2]。

本文中假定在船舶甲板上方放置一定重量的貨物，船舶在波浪中運動狀態下，對貨物的慣性力計算方法進行了較為深入系統的研究，得出了一套較為簡潔的理論計算公式，并應用到實際工程項目中，確保了工程實施的安全性。

1 船舶在波浪中運動的概述

船舶在隨機的、波浪方向紊亂的海上航行和作業時，必然會受海浪的擾動產生振蕩運動。如果把船作為剛體，則這種運動一般應有六個自由度。圖1給出船舶振蕩運動的定義。如取o-xyz為固定在船上的右手坐標系；相對于振蕩運動的船為固定的右手坐標系O-XYZ[3]。這時船（即o-xyz坐標系）相對于O-XYZ坐標系的六個自由度運動是：

（1）沿三個坐標軸的往復振蕩。

X-進退運動； Y-橫蕩運動；

Z-升沉（或垂蕩）運動。

（2）繞三個坐標軸的旋轉振蕩。

Φ-橫搖，繞x軸的旋轉振蕩；

θ-縱搖，繞y軸的旋轉振蕩；

Ψ-首尾搖，繞z軸的旋轉振蕩。

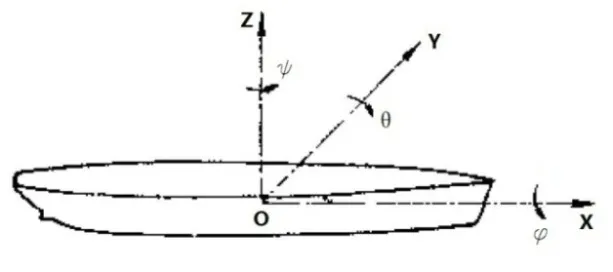
圖1 船舶在波浪中振蕩運動的定義

上述運動按照圖1中所示的箭頭方向取正值，與箭頭方向相反的取負值。

2 慣性力計算

當船舶在波浪中運動時，固定在甲板上方的貨物將隨著船舶運動產生很大的加速度，而加速度本身由角加速度和線加速度兩部分組成。為了保證貨物綁扎固定設計的可靠性以及對貨物本身結構的影響，應考慮其加速度產生的慣性力的影響。通常在求解加速度和慣性力時，考慮以下運動組合情況[1]：

（1）橫搖+垂蕩；

（2）縱搖+垂蕩。

取坐標系方向：x軸沿船長方向（由船首指向船尾），y軸指向船舶右舷，z軸垂直向上，原點取在搖擺中心處。

以下主要針對船舶在上述兩種組合運動狀態下，慣性力計算的詳細推導過程，表1為船舶在波浪中的運動狀態。

表1 船舶在波浪中的運動狀態

2.1 橫搖+垂蕩

最大橫搖發生在共振時候，擾動力的周期與船舶的搖擺周期一致。船舶的橫搖方程式為[3]：

式中：

?：船舶最大橫傾角度；

T?：船舶橫搖周期；

ε?：相位差。

當存在著與速度的一次方成正比的阻力時，共振時的位移相角比擾動力的相角落后此時角加速度達到最大值。

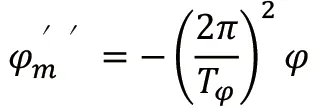
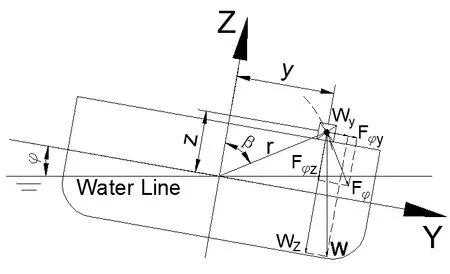
圖2 船舶橫搖時貨物慣性力矢量

圖中：

W：甲板貨物自重；

y：貨物重心至船中縱線的橫向距離；

z：貨物重心至搖擺中心的垂直距離；

r：貨物重心橫搖半徑。

船舶發生橫搖時，甲板貨物在小范圍繞搖擺中心做圓周運動，切向加速度計算公式如下：

根據圖2所示，各參數關系可知：

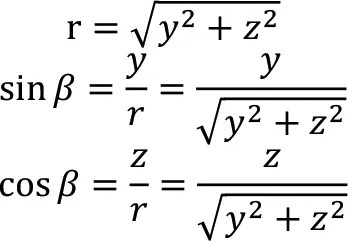
貨物由圓周運動產生的切向力為：

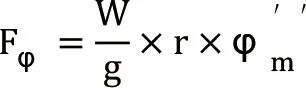
因此，切向力的水平和垂向分量分別為：

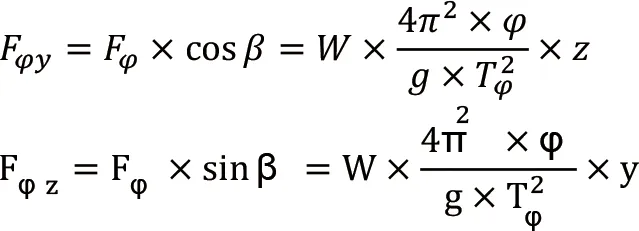
貨物重量在y與z方向的分量分別為：

綜合以上公式，僅考慮船舶橫搖運動時，在船寬方向和垂直方向上的總的慣性力之和：

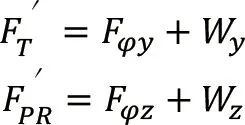
由于船舶在波浪中，發生橫搖運動的同時也會存在垂蕩運動。考慮垂蕩加速度對慣性力的疊加影響，甲板貨物在船寬方向和垂直方向的最大慣性力計算公式分別為：

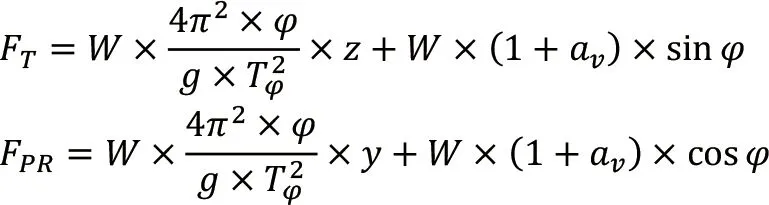
2.2 縱搖+垂蕩

最大縱搖發生在共振時候，擾動力的周期與船舶的搖擺周期一致。船舶的縱搖方程式為[3]：

式中：

θ：船舶最大縱傾角度；

Tθ：船舶縱搖周期；

εθ：相位差。

當存在著與速度的一次方成正比的阻力時，共振時的位移相角比擾動力的相角落后此時角加速度達到最大值。

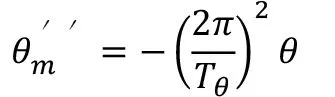
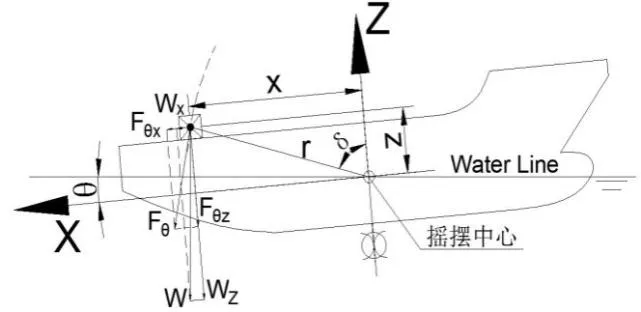
圖3 船舶縱搖時貨物慣性力矢量

圖中：

W：甲板貨物自重；

x：貨物重心至搖擺中心的縱向距離；

z：貨物重心至搖擺中心的垂直距離；

r：貨物重心縱搖半徑。

同理，船舶在縱搖+垂蕩組合運動狀態下，甲板貨物在船長方向和垂直方向的最大慣性力計算公式分別為：

3 慣性力公式實際工程應用

上述慣性力計算公式，通常在海洋工程結構物運輸綁扎設計中使用，較為典型的是固定式平臺鋼樁運輸的綁扎固定設計。下面以某國外實際鋼樁運輸設計工程項目為例，簡單介紹上述慣性力計算公式的應用。

該項目中共有兩種類型的鋼樁，在駁船甲板上的布置及詳細重心信息，見圖4。

圖4 鋼樁布置圖及重心位置信息

類型1（P1～P8）：重量為323.8噸/根；類型2（P9～P12）：重量為331.4噸/根。

工程項目使用的駁船主尺度為：

船長：110m；型寬：32m；型深：7.5m。

駁船實際在波浪中的運動狀態，見表2。

表2 駁船實際運動狀態

根據駁船空船重量重心和鋼樁重量重心信息，以及駁船艙室壓載情況，參考相關規范使用MOSE S軟件求解出駁船的實際搖擺中心，詳細位置見圖5。

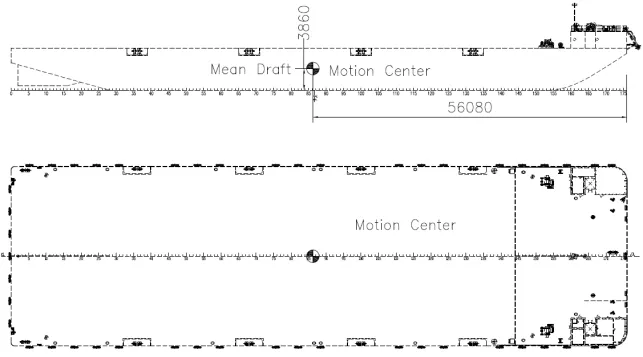
圖5 駁船實際搖擺中心

綜合上述計算結果，代入到慣性力計算公式中可得：

3.1 橫向力

FT-P1/P2/P3/P4=156.638MT，

FT-P5/P6/P7/P8=169.387MT，

FT-P9/P10=160.315MT，

FT-P11/P12=173.363MT。

3.2 縱向力

FL-P1/P2/P3/P4=98.943MT，

FL-P5/P6/P7/P8=106.914MT，

FL-P9/P10=101.266MT，

FL-P11/12=109.423MT。

3.3 垂向力

根據鋼樁的布置及重量信息，可以分為6堆，即P1&P5、P2&P6、P3&P7，P4&P8，P9&P11和P10&P12。按照 3中所述的兩種工況組合的方式分別計算垂向力，再取兩者之間的較大值作為設計載荷。另外，由于鋼樁在駁船上的擺放形式為兩層，因此計算垂向力時，應將上下兩層的鋼樁重量求和。根據上述垂向力計算原理，最大垂向力計算結果如下：

3.3.1 橫搖+垂蕩

FPR-P1&P5=831.654MT，

FPR-P2&P6=806.155MT，

FPR-P3&P7=780.657MT，

FPR-P4&P8=755.159MT，

FPR-P9&P11=825.248MT，

FPR-P10&P12=851.345MT。

3.3.2 縱搖+垂蕩

根據上述垂向力計算公式可知，前4堆鋼樁（P1&P5、P2&P6、P3&P7和P4&P8）在縱搖+垂蕩工況下，其垂向力計算結果相同，即為FPP-1=815.168MT。

后2堆鋼樁（P9&P11和P10&P12）在縱搖+垂蕩工況下，其垂向力計算結果相同，即為FPP-2=842.049MT。

最后，使用上述計算得到的橫向力、縱向力和垂向力結果，進行鋼樁固定以及駁船船體強度的校核，確保設計滿足相關規范要求。

4 結論

本文對波浪中船舶慣性力的計算方法進行了深入系統的研究，詳細地介紹了理論計算方法的公式推導原理，得出了一套較為簡潔的理論計算公式。通過實際工程項目的使用，驗證了該套慣性力計算公式的可行性，得到了海洋工程行業內的普遍認可，確保了工程實施的安全，并為實際工程的實施提供了理論依據，同時也避免了許多繁瑣的計算過程。