基于關聯維計算的軟件失效混沌識別研究

錢 麗，胡 俊，王美榮，沈桂芳, 陳 平

(安徽新華學院 信息工程學院,安徽 合肥 230088)

基于關聯維計算的軟件失效混沌識別研究

錢 麗，胡 俊，王美榮，沈桂芳, 陳 平

(安徽新華學院 信息工程學院,安徽 合肥 230088)

針對大數據環境下軟件失效行為的復雜性問題，提出了一種基于關聯維數的軟件失效混沌識別算法.通過計算軟件失效數據是否具有關聯維特征來驗證失效的混沌性，利用相空間方法重構軟件失效系統，驗證了軟件失效行為的混沌性.實驗結果表明，混沌關聯維算法能夠有效識別軟件失效的混沌性，精確地描述軟件失效行為的無序性和無規則性，同時也能解決復雜軟件系統失效、大數據混沌性這類復雜問題.

大數據；軟件失效；關聯維；混沌識別

隨著互聯網、云計算技術的不斷創新與發展，數據呈現爆炸式的增長，軟件系統也變得日益復雜.軟件安全性問題一直以來都是企業在運營過程中關注的焦點問題，復雜軟件系統給企業的軟件安全提出了更高的要求[1-2].目前比較常用的研究方法是通過對軟件失效行為的分析，挖掘出復雜軟件系統內在的本質演化規律[3].國內研究中，YANG等[4]采用疊加NHPP模型極大似然估計法來研究軟件失效行為；程躍華等[5-6]采用主成分分析法研究軟件失效機理，解決軟件可靠性度量存在的多重共線性問題；臺灣LIN等[7]提出性能模型演示的實驗方法進行軟件失效分析；樓俊鋼等[8]采用主成分回歸算法和支持向量回歸等核函數回歸估計方法研究軟件失效行為.國外研究中，INOUE等[9]提出離散型軟件可靠性模型，不同于連續時間上的軟件可靠性模型，較好解釋軟件失效行為；LANDONA等[10]開發貝葉斯推理模型和強化泊松過程模型，并且實施于實際軟件故障數據預測模型的過程；ZHENG等[11-12]研究者提出基于神經網絡的非參數式建模方法研究軟件失效行為，這種方法不同與以往基于一些主觀假設條件的SRGM，對軟件可靠性的度量、預測的精度有很大的提高，但對軟件失效行為的本質分析不夠透徹.

以上研究主要基于概率論與數理統計方法，假定軟件失效行為符合某種概率分布，使用可靠性隨機模型來分析軟件失效過程，這種研究觀點與方法具有一定的主觀性，較難解決軟件失效、復雜軟件系統失效行為的混沌性問題.大數據環境下的軟件失效行為不僅具有隨機性，也具有確定性，軟件失效行為的本質與混沌特性是具有相似性的，雖然受到確定規則的約束，但是其行為卻表現出無序性.因此，本研究將混沌關聯維特征計算應用到軟件失效行為的分析上，比隨機模型更好地描述軟件失效行為的無序性和無規則性，同時也能夠解決軟件失效、大數據混沌性這類復雜的問題.

1 混沌識別特征量分析

復雜軟件系統失效行為的演化過程中，可以將測試人員、軟件和運行環境看做一個復雜混沌系統，系統中各個分量之間相互影響作用，復雜軟件系統不斷地向前演化，在此過程中應用混沌時間序列分析軟件失效行為的演化規律.軟件失效的混沌現象是指系統在確定系統中貌似隨機的不規則運動，其行為表現出不可預測，無序的狀態.軟件失效行為的混沌特征通常表現為無明顯規則和次序、非同期性的復雜折疊和扭曲，軟件失效行為的混沌識別通過計算Lyapunov指數和關聯維數等混沌特征量來判斷軟件失效數據是否具有混沌性.

1.1 Lyapunov指數

在對軟件失效行為的分析過程中，所收集的失效數據只是整個軟件失效系統的局部觀測值，如果要研究系統的演化規律，就要計算嵌入維、時間延遲，重構與原空間微分同胚的相空間.相空間是一個六維假想空間，其中動量和空間各占三維.物理學中的相空間由系統的狀態點組成，相空間的維數由質點系的“自由度”個數來決定.若用x來表示質點所在的位置，那么質點速度由x對時間t的一階導數xdx/dt表示，(x，y)表示系統的一個狀態點，所有狀態點的集合就構成了系統的相空間.通過重構相空間可以挖掘系統的演化規律.

混沌系統的運動軌道具有初值非常敏感性，相空間中初始距離靠近的兩條軌跡以指數速率發散，通過Lyapunov指數形式描述.初始兩點在一維動力系統xn+1=F(xn)中迭代后，它們的分合程度取決于|dF/dx|的值：大于1則兩點分離；反之則靠攏.假設初始點x(t0)附近有一點x(t0)+Δx(t0)，則經過n次迭代后，

x(tn+1)+Δx(tn+1)=f[x(tn)+Δx(tn)]≈

f[x(tn)]+Δx(tn)f′[x(tn)]

因此，

Δx(tn+1)=Δx(tn)f′[x(tn)]

(1)

其中，t0和tn分別為初始時間和當前時間.假設相空間兩點軌跡的初始距離為|Δx(t0)|，經過n次迭代后兩點的距離為|Δx(tn)|，由上面式(1)得出：

|Δx(t0)|exp(λtn)

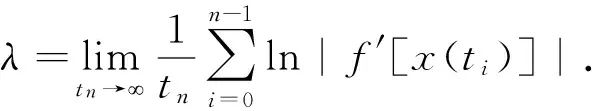
系統的Lyapunov指數, 當λ<0時，則系統是穩定的；λ=0時，則系統是周期的；λ>0時，則系統是混沌的.

1.2 關聯維數與嵌入維數

大數據環境下的軟件系統是確定的，系統的變化狀態由若干變量決定，其中變量的個數即為系統的維數.混沌系統雖然在高維空間上表現無序、無規則，但是由于相空間的收縮，系統中的自由活動將越來越少，而相空間聯系和整體約束越來越強，最終趨向于低維空間的極限，也就是所謂的奇異吸引子.如果奇異吸引子存在于軟件失效的觀測時間序列{x(t)}中，關聯指數D隨著嵌入維數m的增大而增加，直至觀測到關聯指數D收斂為一飽和值時，那么可以用關聯維數描述此吸引子的特征.關聯維通常采用關聯積分計算觀測變量前后的相互關聯性，從而描述信號的確定程度和規律.

本研究借助G-P算法計算大數據環境下的軟件失效數據的關聯維數，其算法主要思想是選擇不同的領域半徑r，分別計算相應的C(r)，從而得到D.當求得數據的飽和值后，根據失效數據的嵌入維數(m≥2d+1)，即可確定維數m.復雜軟件環境下混沌系統在高維空間是無序的，但當其投射到低維空間時，就會得到規律性的軌跡，在這個過程中，系統的軌跡也會產生變化.混沌運動表現出的特征在很多方面，例如，某些點雖然在高維空間中相鄰，但是投射到低維空間后卻不相鄰；而某些在高維空間不相鄰的點投射到低維空間時卻相鄰，這也是混沌運動表現出的特征.在重構系統相空間的時候，通常去除這些偽鄰居點，根據復雜環境下混沌系統的這種幾何原理來計算嵌入維，其計算步驟如下：假設{Xn}為混沌時間序列，τ為時間延遲參數，針對某個維數d，可以重構向量序列{yi(d)}，

yi(d)表示d維重構所得到的第i個向量.這里定義：

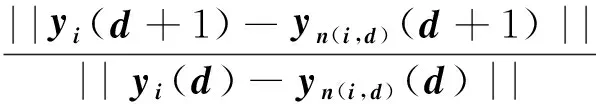
其中i= 1，2，…，N-dτ，||…||為無窮范數.n(i,d)為大于等于1且小于N-d的整數.：yn(i,d)(d)為離yi(d+1)最近的向量.a(i,d)均值定義為).

為了解E(d)的變化，定義：

E1(d)=E(d+1)/E(d)

若吸引子被包含在時間序列中，當維數d大于某個初始值d0時，E1(d)就會停止變化.那么最小嵌入維數為d0+1.

在實際復雜環境中得不到系統的所有分量，所以只有將系統投影到平面或直線上觀測，進而采集系統局部的一個到兩個分量的時間序列，空間維數的估算可以通過嵌入維靠近關聯維數算出.軟件失效的混沌識別，在于關聯維數隨著嵌入維數的增大最終是否收斂，如果收斂于一個穩定值則系統是混沌的；如果不收斂，則是隨機的.軟件可靠性建模通常先收集軟件的失效數據來進行混沌識別，然后通過計算特征量來驗證失效行為的混沌性.

2 軟件失效行為的混沌識別

大數據環境下的復雜軟件系統需要滿足數據量大，數據類型多、運算速度高的特點，并且軟件系統本身具有復雜性和不透明性等特點，使得軟件失效行為變得不確定和難以預測.在實際軟件系統運行過程中，軟件失效的無序性、無規則性，不僅僅具有隨機的特點，更具有混沌的性質，正如現實中大多數系為也是如此.復雜環境下軟件失效行為的混沌性識別過程中，首先收集失效數據，然后驗證失效數據的混沌性，進而分析與預測軟件失效行為.

軟件失效行為的分析和預測的前提是對軟件失效數據的驗證，通過驗證軟件失效數據來分析軟件失效行為的混沌性.失效數據的收集一般在軟件實際運行中進行，分為完全數據和不完全數據兩種類型：

(1)數據集合{y(i) |y(0) =0，i= 1, 2, …, n }為完全數據集合，如果：?：i(i∈{1, 2, …,n}→y(i)-y(i-1) = 1)，其中y(i)為直到時間t(i)時的累積故障數.

(2)數據集合{y(i) |y(0) =0，i= 1, 2, …,p}為不完全數據集合，如果：?i(i∈{1,2,…，p}→y(i)-y(i-1)> 1).

復雜環境下軟件失效行為雖然表現為無序、隨機，但其本質上是具有一定的確定性的，通過計算混沌特征量來判斷軟件失效行為是否具有混沌性，并且借助G-P算法計算關聯維和嵌入維數，進而驗證失效行為的確定性，具體計算過程如下：

(1)對于時間序列x1,x2,…,xn, 假設其中m0為一個較小值，則重構相應的相空間為Yi=(xi,xi+τ,…,xi+(m-1) τ), i = 1, 2, 3,…,M.

(2)計算關聯函數

其中θ(·)為Heaviside函數

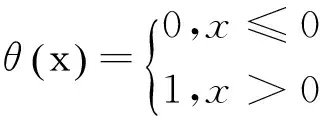
(3)當r→0時，關聯積分與r存在以下關系：

上式參數r的選取需要考慮D能否描述奇異吸引子的自相似結構.

D=lnC(r)/lnr

維數D與函數C(r)需要滿足對數線性關系，并且通過最小二乘法擬合，求出一條最佳直線，該直線的斜率即是對應于m0的關聯維數的估計值d(m0).

(4)重復以上步驟(2)和(3)，繼續增加嵌入維數m，直至關聯維數d(m)不再隨m的增加而增大，并且收斂于一個穩定值狀態，此時求到的d值即為吸引子的關聯維數.如果d值隨m的增長而增長，并不收斂，則表明系統是隨機的.

3 仿真實驗驗證

本次實驗軟件編程環境：Windows7；MATLAB7.0；硬件環境處理器: Intel(R) Core(TM)2 Duo CPU E4500 @2.20GHz.本實驗采用記錄累計失效時間來描述軟件失效行為.首先收集公共測試(Beta)軟件運行過程中的失效數據，然后通過MATLAB7.0語言編程，實現對失效數據關聯維數的仿真，最后分析軟件失效行為是否具有混沌性.

實驗數據1[13]采用美國海軍戰術數據系統NTDS(Naval Tactical DataSystem)公開發表的失效數據.這些數據是從美國海軍戰術數據系統保存的一個實時多處理機系統軟件開發過程的資料中提取的，包括38個不同的模塊，每個程序模塊都經過了開發階段、測試階段和使用階段，數據見表1.

表1 NTDS數據集1
Tab.1 NTDS failure dataset 1

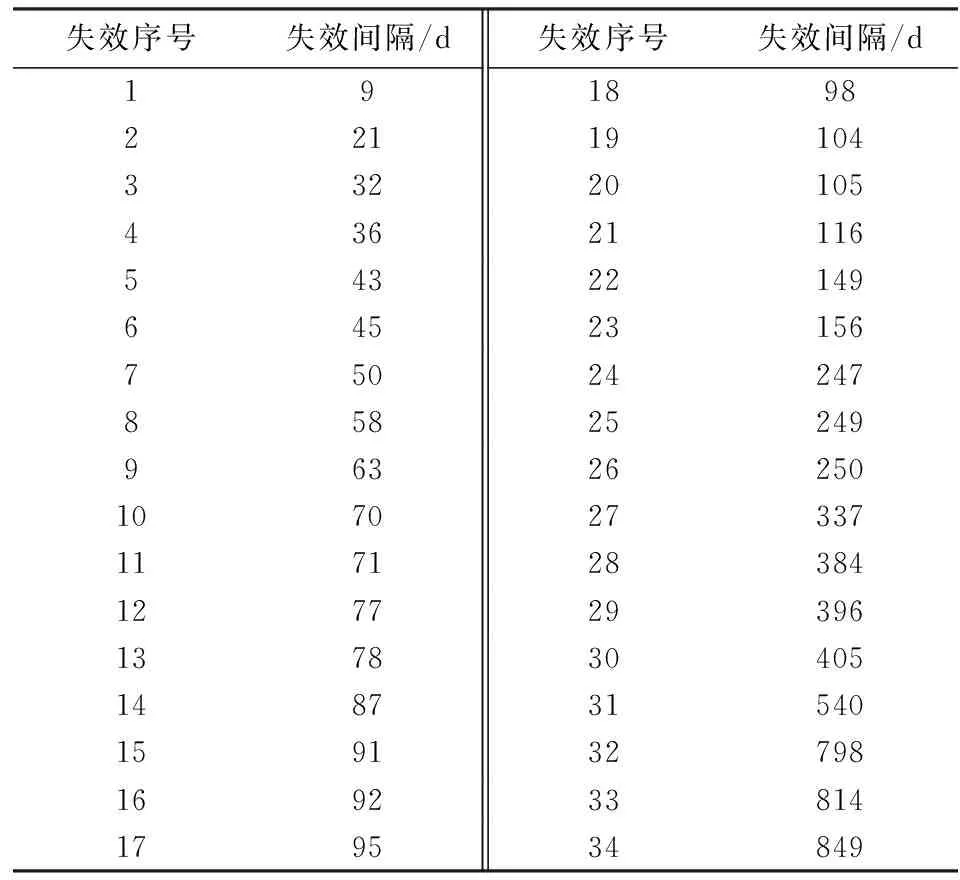
失效序號失效間隔/d失效序號失效間隔/d1918982211910433220105436211165432214964523156750242478582524996326250107027337117128384127729396137830405148731540159132798169233814179534849

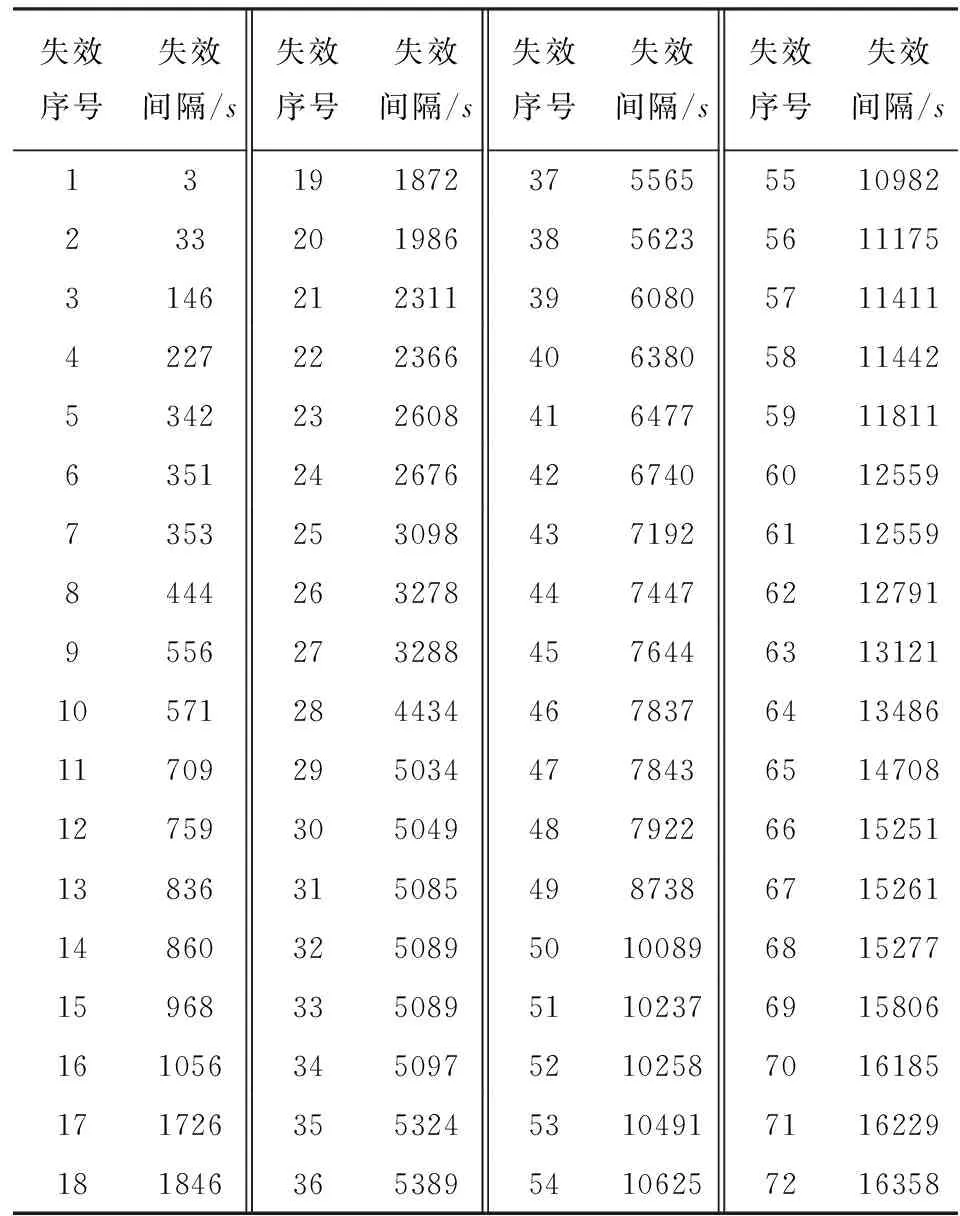
實驗數據集2[13]來源于Musa數據集，由Musa發表(Musa 1990).失效數據由實時命令與控制系統的測試得來，數據集2源于貝爾實驗室，由9個程序員對包含21700條指令的系統的測試得來，系統運行時間為24.6 h，經歷的日歷時間為92 d.數據集包含了72個失效數據，描述了每個失效的CPU時間.整個失效數據集記錄了失效發生的CPU時間，是失效時間數據集，具體見表2.

根據失效數據，利用G-P算法計算失效數據的關聯維和嵌入維，部分編程如下：

G-P算法計算關聯維數

form=min_m:max_m

Y=reconstitution(data,N,m,tau);

%重建矢量空間

M=N-(m-1)*tau;%矢量空間的點數

表2Musa失效數據集2
Tab.2Musafailuredataset2

失效序號失效間隔/s失效序號失效間隔/s失效序號失效間隔/s失效序號失效間隔/s13191872375565551098223320198638562356111753146212311396080571141142272223664063805811442534223260841647759118116351242676426740601255973532530984371926112559844426327844744762127919556273288457644631312110571284434467837641348611709295034477843651470812759305049487922661525113836315085498738671526114860325089501008968152771596833508951102376915806161056345097521025870161851717263553245310491711622918184636538954106257216358

fori=1:M-1

forj=i+1:M

max(abs(Y(:,i)-Y(:,j)));

%計算其余點到點Xi的距離

end

end

max_d=max(max(d));%求出距離最遠的點

d(1,1)=max_d;

min_d=min(min(d));%求出距離最近的點

delt=(max_d-min_d)/ss;%計算r的步長

for k=1:ss

r=min_d+k*delt;

C(k)=correlation_integral(Y,M,r);

%計算關聯積分函數

ln_C(m,k)=log(C(k));%lnC(r)

ln_r(m,k)=log(r);%lnr

end

plot(ln_r(m,:),ln_C(m,:));

hold on;

end

使用Matlab軟件工具運行NTDS 數據集1和Musa數據集2，結果分別如圖1和圖2所示.

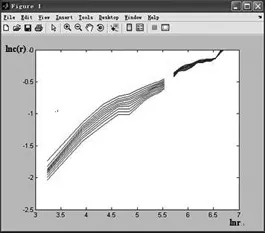
圖1 NTDS 數據的關聯維數Fig.1 The correlation dimension of NTDS data

圖1是NTDS 數據集的運行結果，關聯維數d(m)隨m的增加而增大，最終沒有收斂于一個穩定值，并且關聯維數中間有間斷，說明系統是隨機的.因此，NTDS 數據所表示的系統不具有混沌性.

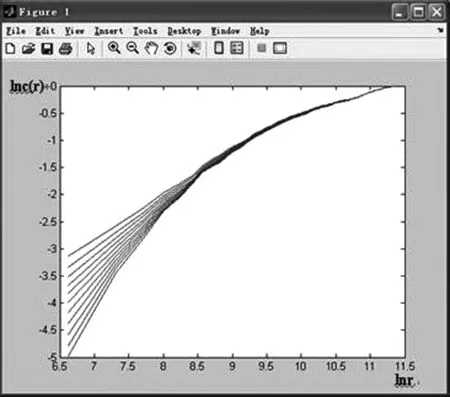
圖2 Musa數據集的關聯維數Fig.2 The correlation dimension of Musa dataset

圖2是Musa數據集2的運行結果，關聯積分曲線隨著嵌入維m的增大而發生相應變化，對其進行線性擬合計算，求得關聯積分曲線斜率就是關聯維.關聯維數d(m)隨m的增加而增大，當m在[1-20]的范圍內增長時，關聯維d最終收斂于一個穩定值.因此，Musa數據集具有混沌性，表明了軟件系統失效行為具有混沌性.

4 結束語

大數據環境下的軟件失效行為不僅具有隨機性，也具有確定性，軟件失效行為的本質與混沌特性是具有相似性的，雖然受到確定規則的約束，但是其行為卻表現出無序性.

本文提出一種基于關聯維數的軟件失效混沌識別算法，通過計算軟件失效數據是否具有關聯維特征來驗證失效的混沌性，利用相空間方法來重構軟件失效系統，定性定量地驗證了軟件失效行為的混沌性.實驗表明，混沌特征量算法能夠有效識別軟件失效的混沌性，突破了軟件失效分析一貫使用隨機理論和數理統計方法的局限, 更加精準地描述大數據環境下的軟件失效行為的無規則性和無序性，并且解決了軟件失效、大數據混沌性等軟件可靠性復雜問題，為大數據環境下的軟件失效行為的研究帶來了新的方法和思路.

[1]苗放.面向數據的軟件體系結構初步探討[J]. 計算機科學與探索,2016, 10(10):1351-1364.

[2]李國杰, 程學旗. 大數據研究:未來科技及經濟社會發展的重大戰略領域——大數據的研究現狀與科學思考[J]. 中國科學院院刊, 2012, 27(6):5-15.

[3]汪北陽, 呂金虎. 復雜軟件系統的軟件網絡結點影響分析[J]. 軟件學報, 2013, 24(12):2814-2829.

[4]YANG J F, ZHAO M. Maximum likelihood estimation for software reliability with masked failure data[J]. Journal of Systems Engineering & Electronics, 2013, 35(12):2665-2669.

[5]程躍華, 崔艷. 組合模型在軟件可靠性預測中的建模與仿真[J]. 計算機仿真, 2011, 28(6):371-374.

[6]劉克,單志廣,王戟,等.“可信軟件基礎研究”重大研究計劃綜述[J]. 中國科學基金, 2008, 22(3):145-151.

[7]LIN C T, HUANG C Y. Enhancing and measuring the predictive capabilities of testing-effort dependent software reliability models[J]. Journal of Systems & Software, 2008, 81(6):1025-1038.

[8]樓俊鋼, 蔣云良, 申情,等. 軟件可靠性預測中不同核函數的預測能力評估[J]. 計算機學報, 2013, 36(6):1303-1311.

[9]INOUE S, HAYASHIDA S, YAMADA S. Toward Practical Software Reliability Assessment with Change-Point Based on Hazard Rate Models[C]//Computer Software and Applications Conference.IEEE Computer Society, 2013:268-273.

[10]LANDON J,OZEKICI S, SOYER R. A Markov modulated Poisson model for software reliability[J]. European Journal of Operational Research, 2013, 229(2):404-410.

[11]ZHENG J. Predicting software reliability with neural network ensembles[J]. Expert Systems with Applications An International Journal, 2009, 36(2):2116-2122.

[12]BARU C, BHANDARKAR M, CURINO C, et al. Discussion of BigBench: A Proposed Industry Standard Performance Benchmark for Big Data[M].[s.l.]:Springer International Publishing, 2014:44-63.

[13]LYU M R. Handbook of Software Reliability Engineering[M/OL].Hong Kong: Department of computer science and engineering, Chinese University Hong Kong,2005[2016-11-23].http://www.cse.cuhk.edu.hk/～lyu/book/reliability/.

Researchonthechaosidentificationofsoftwarefailurebehaviorbaseoncorrelationdimensioncalculation

QIAN Li，HU Jun，WANG Mei-rong,SHEN Gui-fang，CHEN Ping

(Institute of Information Engineering，Anhui Xinhua University, Hefei 230088, China)

In view of the disorder of software failure behavior in large data environment, a software failure identification method based on chaotic correlation dimension is proposed. With the help of the G-P algorithm, the characteristics of the correlation dimension and the embedding dimension of the failure data are calculated, and the uncertainty of the software failure data is determined by the chaotic characteristic quantity. The experimental results show that the chaos correlation dimension algorithm not only can effectively identify software failure,and accurately describe the software failure behavior disorder and irregular, but also can solve the complex software system failure, and big data chaos of this kind of complex problem.

big data； software failure；correlation dimension；chaos identification

2016-12-02

安徽省教育廳自然科學基金重點項目(KJ2014A100，KJ2015A300，KJ2016A304)；安徽省質量工程項目(2015ckjh113)

錢麗，女, wulianchongjing@qq.com

1672-6197(2018)01-0021-05

TP309.2

A

(編輯：姚佳良)