淺談高中數學中的不等式問題

歐陽昱燾 長沙市長郡濱江中學

一、不等式在高中數學學習中的重要地位

在高中數學理論體系中，不等式是數學基礎理論的重要組成部分，而不等式問題則貫穿了整個高中數學學習，例如，不等式可以應用在函數問題、三角函數問題、幾何問題、平面向量問題、數列問題等，不等式問題的考查也集中在上述幾個方面的問題。不等式問題的分析和解答集抽象性、復雜性、邏輯性為一體，是高中數學學習過程中較難掌握、較為棘手的問題，通常也出現在高考數學的壓軸題當中。同時，在針對不等式問題分析和學習的過程中，同學們不僅可以熟悉不等式問題的基本概念，而且還能培養自身數形結合、函數與方程等思想，養成獨立思考的自主學習習慣和能力。因此，熟練掌握高中數學各種類型的不等式問題的解法，不僅能夠提高高考數學成績，還能夠鍛煉同學們的動手計算能力和邏輯思考能力，意義重大。

二、高中數學不等式問題的類型與其對應的解法探索

縱觀近十年的全國各個省份的高考數學題目，不難發現，不等式問題往往很少單獨命題，出題人常常將不等式問題與其他知識點（如：函數求導、解析幾何、數列等問題）相結合，以不等式為解題工具來求定義域、函數單調性、未知數的取值范圍、函數極值問題函數最值問題等內容。因此，高中數學不等式問題的出題方式和考查內容主要為一下兩個方面：一是直接考場不等式的相關內容，考查方式較為直接；二是引導學生以不等式作為工具，對其他重要知識點進行考查，這也是高考數學的重要考點。下面本文將列舉不同類型的不等式問題并進行解法探索。

1.不等式的性質判斷與應用

高中數學不等式的基本性質主要有：（1）對稱性；（2）傳遞性；（3）乘法單調性；（4）加法單調性；（5）同向不等式可加性；（6）同向正值不等式可乘性；（7）正值不等式可乘方；（8）正值不等式可開方；（9）倒數法則。考查的重要不等式主要有：（1）基本不等式；（2）柯西不等式；（3）絕對值不等式；（4）排序不等式；（5）貝努力利等式等。高考命題人往往將不等式的基本性質和重要不等式與其他主干知識點相結合進行交匯考查。

例題1：下面四個條件中，使 ba＞ 成立的充分而不必要的條件是（ ）.

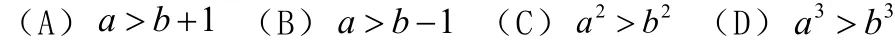
分析：此題出自2011年全國卷，主要考查不等式充要條件的判斷，在解題過程中還要運用好同向不等式可加性和正值不等式可乘方等不等式的性質，通過逐項驗證可解的答案為（A）。

例題2：若0＞＞ba，0＜＜dc，則一定有（ ）.

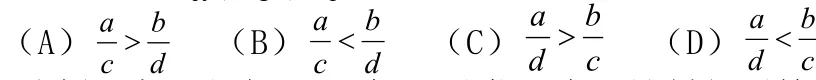
例題3：將離心率為 1e的雙曲線C的是半軸長a和虛半軸長b（ba≠）同時增加)0(＞mm個單位長度，得到離心率為 2e 的雙曲線C ，則（ ）

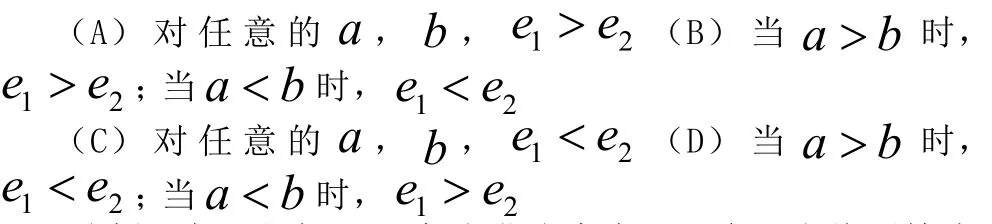
分析：此題出自2015年湖北省高考題。命題人將不等式的基本性質與圓錐曲線相結合，要想解答這道題，答題者不僅要理解不等式的基本性質和圓錐曲線的基本性質，還要將兩個不同的知識點相聯系，是一道典型的不等式問題。

（由解題過程可知，盡管這道高考題看起來非常抽象，同時將圓錐曲線與不等式問題相結合，增加了解題的復雜性，但是如果在審題和分析時明確命題人的出題思路，將兩個看似不相關的考點合理的聯系起來，解題難度就會大大下降。）

2.不等式的證明問題

在高考數學中，不等式的證明常常作為壓軸題出現，可見對學生的邏輯思考能力和判斷分析能力是個有效的考查。這就要求學生在解題過程中要學會通過條件分析問題，通過問題與條件的關系推導出兩者之間的橋梁，進而進一步求解。

（此題出自2011年安徽省高考題，是證明絕對值不等式問題，考綱要求學生要會用比較法、分析法、綜合法等證明絕對值不等式。）

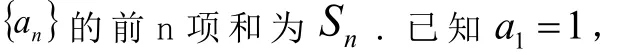
證明：①②的解題過程略。

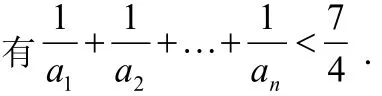
三、總結

總之，通過以上幾個例題可以看出，考題的形式和內容，以及知識點的考查方式都千變萬化，近年來不少創新題涌現，不同類型的知識點之間往往會相結合進行出題。但是，俗話說“萬變不離其宗”，所謂的“宗”，在高中數學就是指解題過程中的數學思想，雖說命題人出題形式變化莫測難以捉摸，但是其考查的數學思想確實亙古不變的，學生在高中數學學習過程中培養一個好的數學思想方法，有利于領悟題目所蘊含的數學思想，進而提高解題效率，得出分析問題的處理方法。