怎樣尋找解題的思維起點

楊春華

解題就是“解決問題”，即求出數學題的答案.這個答案在數學上也叫“解”.所以，數學解題就是找出數學題的解的思維過程.解題過程就是根據問題條件，利用相關的數學基本知識、基本技能、基本思想和活動經驗，有計劃、有步驟、有目的地進行邏輯推理活動.它通常有4個階段：理解題意、思路探求、書寫表達、回顧反思.要快速準確地解題，選擇準確的、科學的思維起點至關重要.為了便于同學們快速準確地解決數學問題，本文將以圓中的重點題型為例，對尋找初中數學解題思維起點的策略進行簡單的分析，以期對同學們有一定的啟迪與思考.

一、直接將題設條件作為思維起點

有同學在審題時不認真，沒看清題目的條件，導致解題無從下手.防止這種情況出現的方法是，在閱讀時放慢速度，對每一個條件盡可能發散思維，思考由每個條件可以得到哪些結論，再將這些結論進行融合，找到相互間的關聯，從而達到解決問題的目的.

例1如圖1，已知AB是⊙O的直徑，點P在BA的延長線上，PD與⊙O相切于點D，過點B作PD的垂線交PD的延長線于點C，若⊙O的半徑為4，BC=6，則PA的長為（ ）.

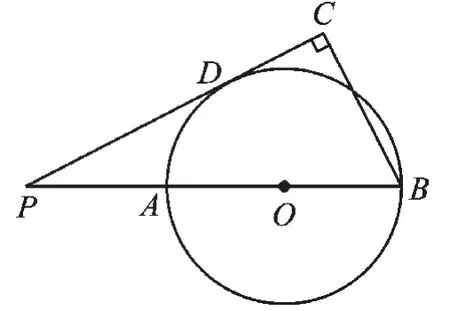
圖1

【分析】本題考查了圓的切線性質、三角形相似條件及性質的相關知識.本題要求線段PA的長度，只需連接切點D與圓心O，則由切線性質即得OD⊥PC，再結合BC⊥PC，得結論OD‖BC，利用△POD∽△PBC的對應邊成比例求出線段PA長度即可.有部分同學由于沒準確提取條件“PD與⊙O相切于點D”中的“點D是切點”信息，而不能快速聯想“看切點，連圓心，得垂直”這一常見添加輔助線思路.

【解答】解：連接OD.∵PD切⊙O于點D，

∴OD⊥PC，

又∵BC⊥PC，

∴OD‖BC，

∴△POD∽△PBC，

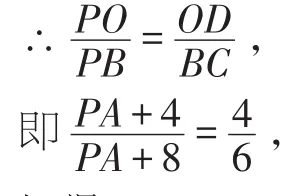
解得：PA=4.

故答案選：A.

【點評】解決數學問題，常常借助條件作為思維的起點.特別是數學中的幾何問題，可以采用邊閱讀邊在圖上標記條件的方法，并將隨之而得的結論寫（畫）在圖形的旁邊，再將這些結論進行融合，找到相互間的關聯，從而發現解決問題的途徑，達到解決問題的目的.

二、挖掘題設中的隱含條件作為思維起點

有些數學問題常常需要挖掘題設中的隱含條件，而圓中的隱含條件往往是一些基本圖形.這就需要我們熟悉這些基本圖形，將復雜圖形轉化為幾個基本圖形的疊加.將這些隱含的基本圖形作為思維的起點，可以使題設條件明朗化、具體化，從而達到明晰解題方向、尋求最佳解題方案的目的.

例2如圖2，在正方形ABCD中，E是AB上一點，連接DE.過點A作AF⊥DE，垂足為F.⊙O經過點C，D，F，與AD相交于點G.

（1）求證：△AFG∽ △DFC.

（2）若正方形ABCD的邊長為4，AE=1，求⊙O的半徑.

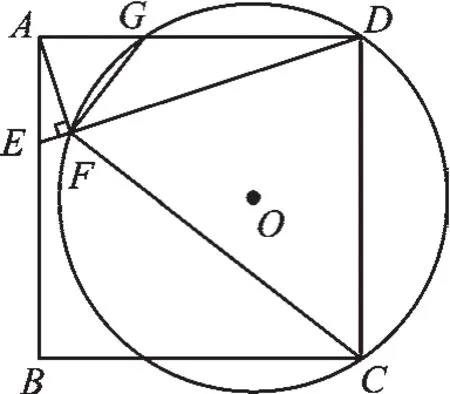
圖2

【分析】本題考查了正方形的有關性質、圓內接四邊形的性質、三角形相似條件及性質、直角三角形勾股定理的相關知識.第一小題欲證△AFG與△DFC相似.根據圓內接四邊形性質及鄰補角概念，可得∠AGF=∠DCF，再利用垂直定義、正方形性質、同角的余角相等的相關知識，可得∠GAF=∠CDF，從而第一問得證.第二小題欲求⊙O半徑，則可先求⊙O直徑，而借助第一問三角形相似及△AED中“母子三角形”相似所得對應邊成比例，可得線段AG=AE=1，再由勾股定理求得圓的直徑而得半徑.有部分同學看不出隱含在題目圖形中的基本圖形：圓內接四邊形及“母子三角形”，導致題設條件不明朗、不具體，不能達到明晰解題方向、快速尋求解題方案的目的.

【解答】證明：（1）因為在正方形ABCD中，∠ADC=90°，

則∠CDF+∠ADF=90°，

∵AF⊥DE，∴∠AFD=90°，

∴∠DAF+∠ADF=90°，

∴∠CDF=∠DAF.

∵四邊形GFCD是⊙O的內接四邊形，

∴∠FCD+∠DGF=180°，

又∵∠FGA+∠DGF=180°，

∴∠FCD=∠FGA，

∴△AFG∽△DFC.

解：（2）如圖3，連接CG.

∵∠EAD=∠AFD=90°.

∠EDA=∠ADF，

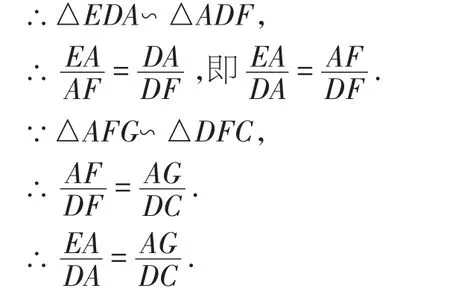
∵在正方形ABCD中，DA=DC，

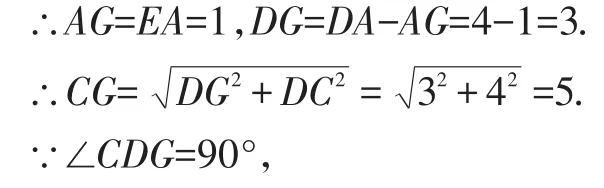
∴CG是⊙O的直徑.

圖3

【點評】利用平時數學知識的學習與積累，將一些圖形的性質概括與抽象成一些易記的基本圖形，并提煉出復雜圖形中的基本圖形是熟練運用這種方法的關鍵.迅速地分析出復雜圖形中的基本圖形，需要平時概括歸納能力的培養.

三、從問題的結論出發，確定思維的起點

初中數學中有些問題的結論不僅是解題的終點，也是解題的起點，調控著解題的全部思維過程.解題中若能恰如其分地用好這些結論的特征，并以此為突破口來確定思維的起點，常常有意想不到的效果.

例3如圖4，AB為⊙O的直徑，點C在⊙O上，AD⊥CD于點D，且AC平分∠DAB.求證：（1）直線DC是⊙O的切線；（2）AC2=2AD·AO.

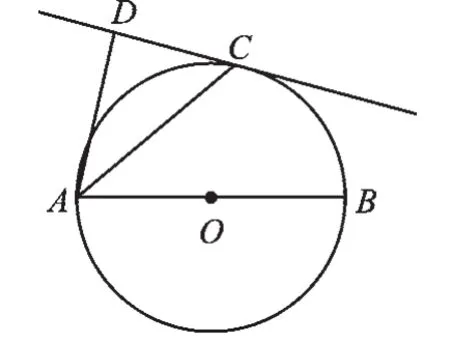
圖4

【分析】本題考查了圓的切線的判定方法、相似三角形的判定及性質.

第一小題欲證直線DC是⊙O的切線，僅需連接OC，證明OC垂直于DC即可.

第二小題欲證AC2=2AD·AO，而AB=2AO，則僅需證AC2=AD·AB.將其轉化為比例式，再證△ADC∽△ACB即可.

【解答】證明：（1）如圖5.連接OC.

∵AD⊥CD于點D，

∴∠ADC=90°，

∵∠ADC+∠DAC+∠ACD=180°，

∴∠DAC+∠ACD=90°，

∵OA=OC，

∴∠OAC=∠OCA，

∵AC平分∠DAB，

∴∠DAC=∠OAC，

∴∠DAC=∠OCA，

∴∠OCA+∠ACD=90°，

即∠OCD=90°，

∴OC⊥CD，

∴直線DC是⊙O的切線.

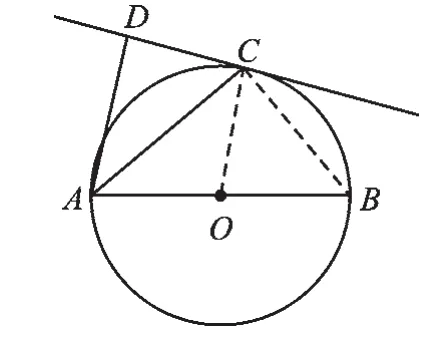
圖5

（2）如圖5.連接BC.

∵AB為⊙O的直徑，

∴∠ACB=90°，

∴∠ACB=90°=∠ADC，

又∵∠DAC=∠CAB，

∴△ADC∽△ACB，

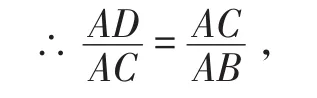
則AC2=AD·AB，

∵AB=2AO，

∴AC2=AD·2AO=2AD·AO.

【點評】對于第二題中線段等積式結論的證明，我們常常將此結論轉化為比例式作為思維的起點；然后對比例式上下（或左右）觀察，找出對應三角形進行相似證明；再結合題設條件，確定判定兩三角形相似的具體證明方法.這類題目常常會將一些線段的倍分關系摻雜其中，這就需要我們能夠根據題設條件將其轉換成具體線段.