見圓思源 “圓”來這樣
武益燕
“圓”這一章的知識點較多,并且往往容易把知識點集合在一起,融合較多的其他知識,在中考中呈現(xiàn)的形式多樣,各種難易程度題目均會出現(xiàn).對于中、高難度題,同學(xué)們?nèi)菀滓姟皥A”色變.本文主要從以下幾方面分析近兩年有關(guān)圓的證明和計算,希望讓曾經(jīng)的不解之“圓”,化為今后的隨“圓”而安.
一、與圓有關(guān)的弧長和面積問題
例1(2018·江蘇鹽城)如圖1,左圖是由若干個相同的圖形(右圖)組成的美麗圖案的一部分.右圖中,圖形的相關(guān)數(shù)據(jù):半徑OA=2cm,∠AOB=120°.則右圖的周長是 cm.
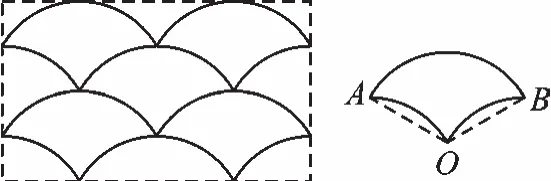
圖1
【解析】如圖2,由圖案的對稱性可知,合在一起可以看成是
所以,圖1右圖周長=2l?AB=2×
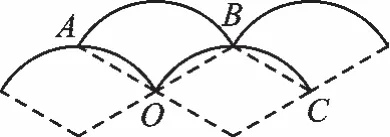
圖2
【點評】這里運用了相等弧的轉(zhuǎn)化思想.另外,本題考查了扇形的弧長公式.
例2(2017·江蘇無錫)如圖3,已知矩形ABCD中,AB=3,AD=2,分別以邊AD,BC為直徑在矩形ABCD的內(nèi)部作半圓O1和半圓O2,一平行于AB的直線EF與這兩個半圓分別交于點E,點F,且EF=2(EF與AB在圓心O1和O2的同側(cè)),則由,EF,?,AB所圍成圖形(圖中陰影部分)的面積等于
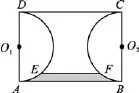
圖3
【解析】如圖4,連接O1O2,O1E,O2F,則四邊形O1O2FE是等腰梯形,過E作EG⊥O1O2,過F作FH⊥O1O2,∴四邊形EGHF是矩形.
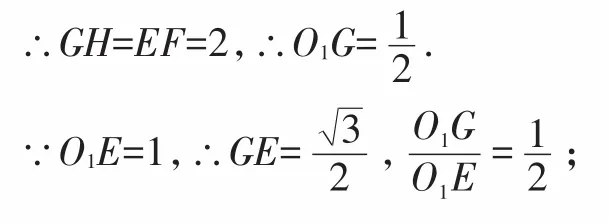
∴∠O1EG=30°,
∴∠AO1E=30°,
同理∠BO2F=30°,

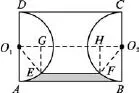
圖4
【點評】求不規(guī)則圖形的面積,常用直接法和間接法.直接法可以利用分割的思想;間接法可以用補圖的思想.本題考查了割補思想、轉(zhuǎn)化思想、數(shù)形結(jié)合思想以及扇形的面積公式.
二、與圓有關(guān)的性質(zhì)問題
例3(2018·浙江溫州)如圖5,D是△ABC的BC邊上一點,連接AD,作△ABD的外接圓,將△ADC沿直線AD折疊,點C的對應(yīng)點E恰好落在圓上.
(1)求證:AE=AB.
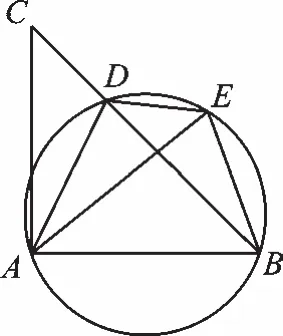
圖5
【解析】證明:(1)∵△ADC沿直線AD折疊,得到△ADE,
∴AE=AC,∠C=∠AED,
∵∠AED=∠ABC,∴∠C=∠ABC,
∴AB=AC,∴AE=AB.
解:(2)如圖6,過點A作AH⊥BE,垂足為H.
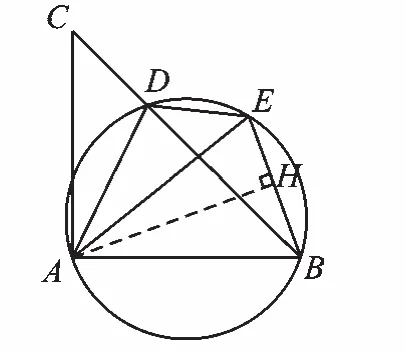
圖6
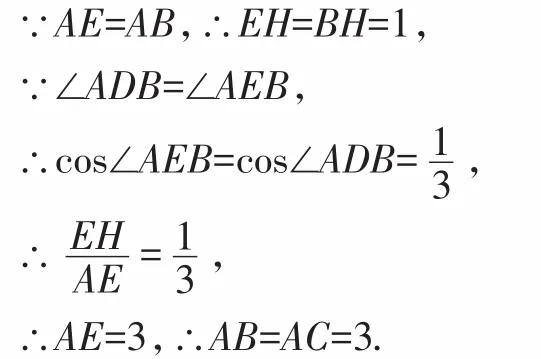
【點評】本題考查了折疊的性質(zhì)、圓周角的性質(zhì)、垂徑定理、銳角三角函數(shù)、勾股定理.重點考查了相等線段、相等角的轉(zhuǎn)化思想.
三、與圓有關(guān)的位置關(guān)系
例4 (2018·江蘇泰州)如圖7,△ABC中,∠ACB=90°,sinA=,AC=12,將△ABC繞點C順時針旋轉(zhuǎn)90°,得到△A′B′C,P為線段上A′B′的動點,以P為圓心,PA′長為半徑作⊙P,當(dāng)⊙P與△ABC的邊相切時,⊙P的半徑為_______.
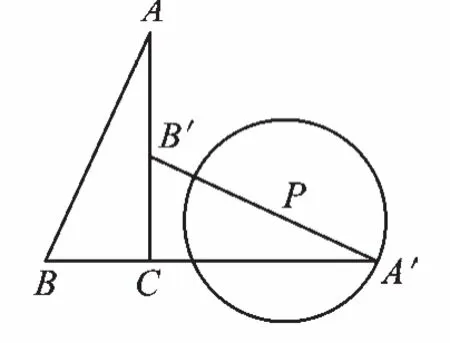
圖7
【解析】①如圖8,當(dāng)⊙P與AC邊相切時,切點為E.連接PE,則PE⊥AC.
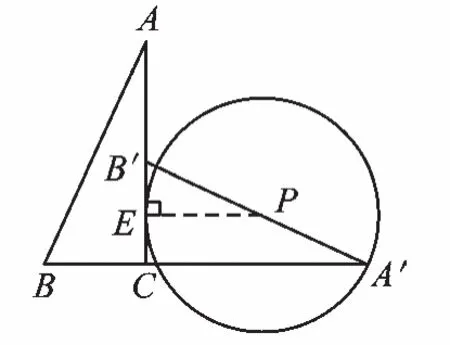
圖8
在Rt△ABC中,
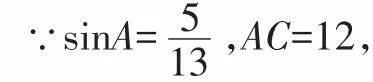
∴AB=13,BC=5.
△ABC繞點C旋轉(zhuǎn)到△A′B′C,
∴A′C=12,B′C=5,A′B′=13.
設(shè)⊙P 半徑為 r,則 EP=r,PA′=r,B′P=13-r.
∵PE⊥AC,A′C⊥AC,∴PE‖A′C,
∴△B′EP∽ △B′CA′,

②如圖9,當(dāng)⊙P與AB邊相切時,延長A′B′交AB于點F.
∵∠A=∠A′,∠AB′F=∠A′B′C,
∴∠AFB′=∠B′CA′=90°,
∴PF⊥AB,∴F為切點.
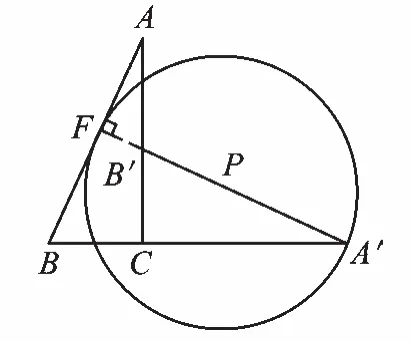
圖9
設(shè)⊙P 半徑為r,則A′F=2r,

【點評】本題主要以三角形和圓為背景,考查了切線的性質(zhì).見切點,連半徑,得垂直,這是在切線問題中的常用方法.另外也考查了分類討論思想、方程思想以及同學(xué)們畫圖、分析圖形的能力.利用垂直,得出三角形的相似,是解決本題的關(guān)鍵.
例5(2017·江蘇鹽城)如圖10,在平面直角坐標(biāo)系中,Rt△ABC的斜邊AB在y軸上,邊AC與x軸交于點D,AE平分∠BAC交邊BC于點E,經(jīng)過點A,D,E的圓的圓心F恰好在y軸上,⊙F與y軸相交于另一點G.
(1)求證:BC是⊙F的切線.
(2)若點A,D的坐標(biāo)分別為A(0,-1),D(2,0),求⊙F的半徑.
(3)試探究線段AG,AD,CD三者之間滿足的等量關(guān)系,并證明你的結(jié)論.
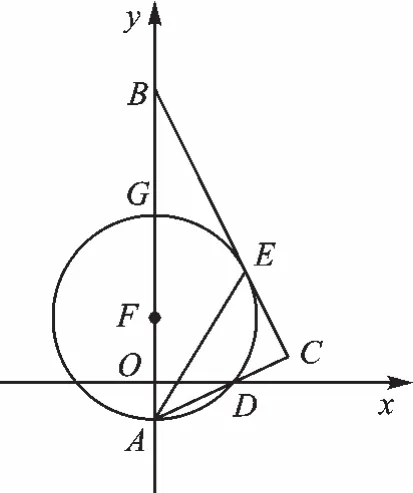
圖10
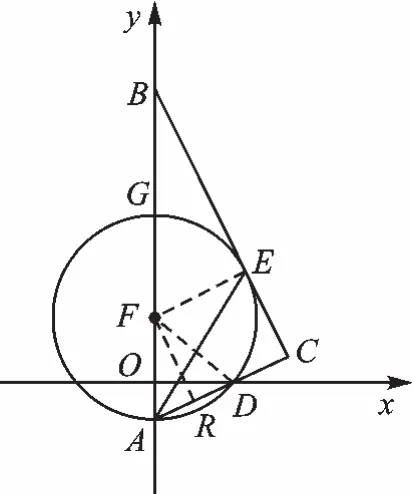
圖11
【解析】證明:(1)如圖11,連接FE.
∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵FA=FE,∴∠FAE=∠FEA,
∴∠FEA=∠CAE,
∴FE‖AC,
∴∠FEB=∠C=90°,
即BC是⊙F的切線.
解:(2)連接FD,設(shè)⊙F的半徑為r,
∵A(0,-1),D(2,0),在Rt△FOD中,F(xiàn)D2=FO2+OD2.
則r2=(r-1)2+22,

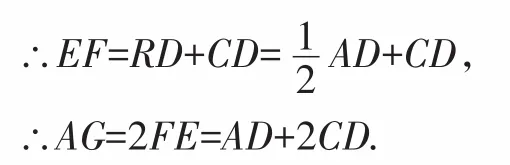
解:(3)AG=AD+2CD.
證明:作FR⊥AD于R,則∠FRC=90°,
又∠FEC=∠C=90°,
∴四邊形RCEF是矩形,
∴EF=RC=RD+CD,
∵FR⊥AD,
∴AR=RD,
【點評】本題重點考查了角平分線的性質(zhì)、矩形的性質(zhì)、切線的判定、垂徑定理、勾股定理等知識,屬于圓的綜合題.

