分位數向量自回歸分布滯后模型及脈沖響應分析

許啟發劉 曦蔣翠俠虞克明

(1.合肥工業大學管理學院,安徽合肥230009;2.合肥工業大學過程優化與智能決策教育部重點實驗室,安徽合肥230009;3.Department of Mathematics,Brunel University,London UB8 3PH,UK)

1 引 言

時間序列分析是一種動態數據分析與處理方法,為揭示決策變量的動態行為特征及其相互之間動態影響關系提供了基本工具,在實踐中獲得了廣泛應用、取得了很好的應用價值,成為一個重要的研究領域.時間序列可以視為隨機過程的一次樣本實現,其分析方法大體經歷了從確定到隨機、從一元到多元、從線性到非線性等發展歷程.隨著差異化統計需求的發展,時間序列平均取值信息難以滿足決策需求,如:VaR風險管理側重于尾部風險特征的描述,人們越來越傾向于研究時間序列完整分布特征的變動規律.為此,在分位數回歸框架下進行多元時間序列分析,能夠揭示在不同分位點處變量之間的異質影響關系,從而提供更多有用信息,便于科學決策,本文對此開展研究.

為研究多個時間序列之間的關系,Sims[1]提出了向量自回歸(vector autoregressive model,VAR)模型.VAR模型采用多方程聯立的形式,通過每一個內生變量對模型全部內生變量的滯后值進行回歸,從而估計全部內生變量的動態關系,避免了變量內生性與外生性的劃分以及模型識別等復雜問題.VAR模型建模過程非常簡單,只需進行兩個關鍵性的選擇:(1)變量選擇,在系統邊界范圍內,選擇關聯關系緊密的變量建立模型系統;(2)滯后階數選擇,在可能整數取值范圍內,選擇能夠揭示變量間真實關系的最優滯后階數.在多元時間序列分析中,VAR模型占據非常重要的地位,一方面它能夠同時捕捉多個時間序列之間的線性依賴關系,準確地預測時間序列的動態變化規律;另一方面它可以為許多其他時間序列分析方法提供基礎,如:基于VAR模型的脈沖響應分析、Granger因果分析、協整分析等.因此,VAR模型在實踐中獲得了廣泛的應用,如:劉向麗等[2]通過高頻數據,使用VAR模型研究了中國期貨市場收益率與交易量之間日內變動模式;王曦等[3]使用VAR模型與脈沖響應分析,比較了各種貨幣政策工具、目標和作用效果,識別反通貨膨脹的貨幣政策有效性;李湘梅等[4]使用VAR模型與脈沖響應分析、方差分解等,研究中國能源消費碳排放影響因素.

然而,以上研究工作都是在均值意義下開展的,只能描述響應變量條件均值的變動規律.按照統計學觀點,均值只是隨機變量分布的局部特征,當響應變量服從非對稱分布或者散布較大時,均值很難具有代表性.完整地描述隨機變量變動規律需要依賴于分布函數.為此,Koenker等[5]提出了分位數回歸,主要目的在于細致地刻畫解釋變量對響應變量整個條件分布的影響.王新宇等[6]考慮金融資產收益與正負收益對分位數沖擊的非對稱性,建立含有非對稱絕對值和斜率設定的AAVS-CAViaR模型,采用混合最優化方法估計模型的參數并進行顯著性檢驗.許啟發等[7]提出了分位數局部調整模型,實證結果表明,在不同分位點處,調整速度與調整方式都呈現出非對稱性.運用分位數回歸方法,史金鳳等[8]對金融市場穩定進行了檢驗,王新宇等[9]描述了在不同分位點處IPO收益率與交易量之間的異質性關系.Xu等[10]更進一步使用非線性分位數回歸方法,研究了美國非線性Phillips曲線,并給出產出缺口變化對通貨膨脹條件概率密度的影響.許啟發等[11]使用神經網絡分位數回歸模擬金融系統的非線性結構,同時結合極值理論彌補非線性分位數回歸對極端尾部數據信息處理能力的不足,并將其應用于極端VaR風險測度.這些研究工作一致表明,分位數回歸能夠彌補均值回歸的不足,可以更加細致地描述經濟規律在不同分位點處的異質效應,從而提供更多有用信息,便于科學決策.

在時間序列分析領域,均值回歸框架下的諸多經典模型與方法,紛紛擴展到分位數回歸框架下.Koenker等[12]將自回歸模型擴展到分位數回歸框架下,提出了分位數自回歸(QAR)模型,其自回歸系數具有分位點依賴性,隨著分位點變化而變化.陳磊等[13]使用分位數自回歸(QAR)模型,對石油期貨收益率的分布特征與石油市場的風險特征進行了定量研究,發現前期油價漲跌對石油期貨收益存在明顯的非對稱影響.Engle等[14]在QAR框架下提出了CAViaR模型,用于描述風險價值(VaR)的變動規律.Xu等[15]研究了QAR模型對金融危機的預測能力,發現CAViaR模型的預測能力優于QAR模型.Gourieroux等[16]研究了動態加性分位數模型,該模型一方面具有很好的自回歸性質,體現分位數的動態效應;另一方面具有很好的包容性,概括了幾類經典的線性與非線性分位數自回歸模型.葉五一等[17]使用動態分位數回歸方法,通過回歸系數函數變化趨勢對金融風險傳染問題進行檢驗和預測.更進一步,Galvao等[18]在QAR模型中引入外生變量,提出了分位數自回歸分布滯后(QARDL)模型.White等[19]將QAR模型擴展到多元情形的向量分析框架下,提出分位數向量自回歸(QVAR)模型,可用于討論不同隨機變量尾部之間的關聯程度.

本文在QVAR模型基礎上,引入外生解釋變量及其滯后項,建立高階分位數向量自回歸分布滯后(QVARDL)模型,該模型不僅能夠考慮內生解釋變量之間的相互影響,而且可以討論外生解釋變量所帶來的在不同分位點處的異質影響,從而將White等[19]的QVAR模型向前推進一步.本文主要開展了四個方面新的研究工作:第一,給出了高階QVARDL(p,q)模型的數學表示及參數估計方法;第二,建立了用于最優滯后階數p與q選擇的信息準則;第三,推導了基于QVARDL(p,q)模型的分位數脈沖響應過程;第四,將QVARDL(p,q)模型及分位數脈沖響應分析應用于解釋美國次貸危機的影響.研究結果顯示:本文的模型與方法能夠同時刻畫多個時間序列在多個分位點處條件分位數之間的關聯關系,可以更加深入地揭示美國次貸危機帶來的影響,實證結果表明:美國次貸危機在世界范圍內產生了深遠影響,但對不同國家(地區)的資本市場在影響程度、影響方式、響應時期等方面有著不同的表現.

2 QVARDL模型

2.1 模型表示

考慮一個由Y1t,Y2t,...,Ynt組成的n×1維向量時間序列,記?t為由生成的直到t時刻的信息集.在給定?t-1時,Yit的條件分位數可以定義為

其中τ(0＜τ＜1)稱為分位點;Fit(y|?t-1)=Pr(Yit≤y|?t-1)為隨機序列{Yit}的條件分布函數;inf{x}表示變量x的下確界.

Koenker等[5]提出了分位數回歸方法,用以估計條件分位數.在時間序列分析中,自回歸是最為常用的一個建模方法,它能夠很好地描述時間序列的動態性.Koenker等[12]將自回歸模型擴展到分位數領域,讓自回歸系數隨著分位點的變化而變化,提出了分位數自回歸(QAR)模型.在QAR模型中,響應變量為時間序列的條件分位數,解釋變量為時間序列的滯后項.更進一步,Engle等[14]在QAR框架下不僅使用時間序列的滯后項,也使用了條件分位數滯后項,提出了CAViaR模型,取得了更好的實證效果.

受Engle等[14]建模理念的啟示,本文將分位數自回歸模型擴展到多元情形,建立分位數向量自回歸分布滯后(QVARDL)模型,同時估計多個時間序列在多個分位點處的條件分位數及其相互之間動態關聯關系.不妨考慮由n個時間序列條件分位數組成的n×1維向量條件分位數QYt(τ)≡Qt(τ)=(Q1t(τ),Q2t(τ),...,Qnt(τ))T,可以建立模型

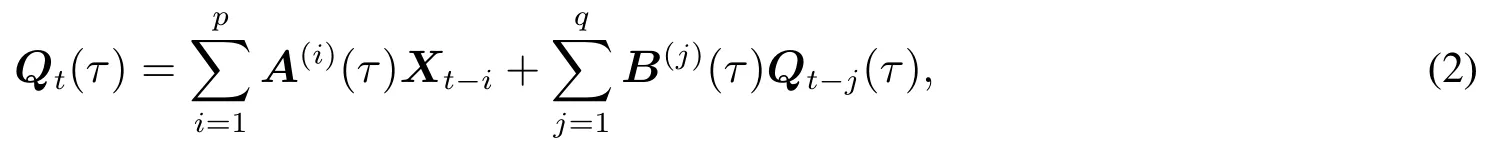
其中X既可以表示由外生變量組成的向量,也可以特指模型內生變量組成的向量X≡Y;p,q分別為滯后階數;A(i)(τ)與B(j)(τ)為影響系數矩陣,依賴于分位點τ的取值,分別定義為

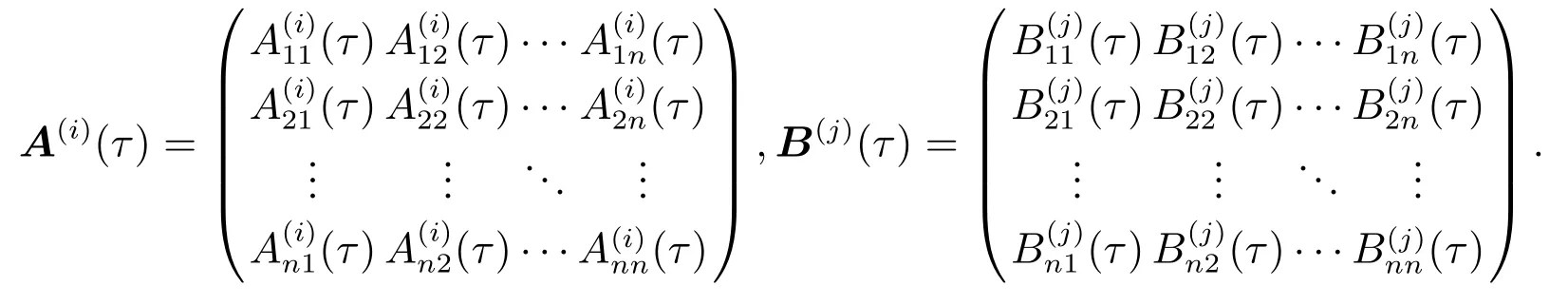
模型表明,向量條件分位數Qt(τ)不僅受到向量時間序列滯后項Xt-i的影響,產生分布滯后效應;同時受到其自身滯后項Qt-j(τ)的影響,產生自回歸效應.不過,模型(2)只是考慮了一個分位點,只能估計第τ個條件分位數.如果同時考慮m個分位點τ1＜τ2＜···＜τm處的向量條件分位數,則可以建立模型

將其表示成矩陣與向量形式

模型(4)與時間序列分析中的自回歸分布滯后模型在形式上完全一致,然而卻存在本質上的區別,這里的響應變量為條件分位數,回歸系數也是依賴于分位點的變化而變化.值得注意,模型(4)是在White等[19]的QVAR模型基礎上引入外生解釋變量的滯后項所得,是其推廣形式,不僅能夠考慮內生解釋變量之間的相互影響,而且可以討論外生解釋變量所帶來的在不同分位點處的異質影響.事實上,模型(4)與Engle等[14]的CAViaR模型也存在顯著差別,至少表現在三個方面:第一,這里的響應變量為向量形式,能夠同時對多個時間序列的條件分位數進行估計,提高了建模效率;第二,這里的分位點為多個分位點,能夠同時考慮在多個分位點處條件分位數的估計,為解決分位數交叉問題提供了可能;第三,這里的回歸系數為矩陣形式,若矩陣中非主對角線上的元素非零,則能夠刻畫不同時間序列之間的相互依賴關系.因此,本文稱式(4)為分位數向量自回歸分布滯后模型,記為QVARDL(p,q).由QVARDL(p,q)模型,可以得到每一個時間序列在各個分位點處條件分位數估計,其中第i個時間序列在分位點τj處的條件分位數可以表示為

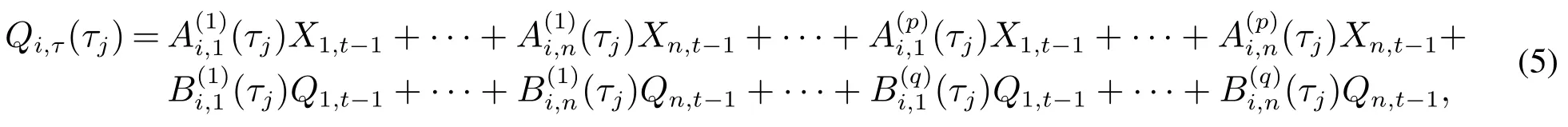
可以看出,QVARDL(p,q)模型不僅描述了時間序列(或條件分位數)自身對自身條件分位數的影響,而且刻畫了來自其他時間序列(或條件分位數)的影響,能夠度量多個時間序列及其條件分位數之間復雜的相互依賴關系.本文建立了更為一般的高階QVARDL(p,q)模型,這一高階模型比White等[19]的一階QVAR(1,1)模型更能體現變量之間的真實依賴關系,從而更加符合實際建模需求.

2.2 模型參數估計

為實現QVARDL(p,q)模型的系數向量θ的估計,需要將其視為一個模型系統,在多個分位點處同時考慮多個時間序列條件分位數之間的關系.為此,對于樣本觀測值Yi,t,i=1,2,...,n;t=1,2,...,T,可以定義損失函數S(θ),并由下式實現模型的參數估計

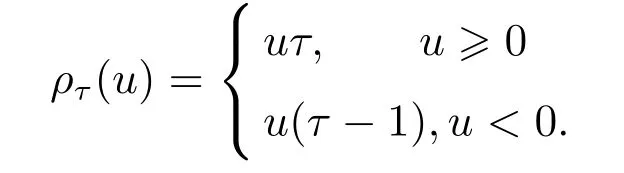
可以證明,式(6)所示的QVARDL(p,q)模型的系數向量估計量具有良好的統計性質:一致性與漸近正態性.

定理1(一致性):對回歸系數估計量與真實參數θ?,有.

證明定理1的證明過程參見附錄2.

定理2(漸近正態性):漸近服從正態分布,滿足,其中”表示依分布收斂;;▽θ為關于θ的向量偏導數,1{·}為指示函數.

證明定理2的證明過程參見附錄3.

2.3 模型定階

在QVARDL(p,q)模型中,滯后階數p與q的選擇非常重要,可以通過信息準則實現這一目的.信息準則最早由Akaike[20]和Schwarz[21]提出,在實踐中獲得了廣泛的應用,其核心思想為:在模型使用變量數目與模型擬合效果之間進行權衡,以求達到通過最簡單的模型結構給出最佳解釋效果之目的.傳統的AIC和BIC信息準則定義如下:

其中L,k,n分別表示模型似然函數,待估參數個數以及樣本量.

為解決QVARDL(p,q)模型定階問題,本文在分位數回歸框架下給出AIC和BIC定階準則如下:

其中S(θ)為按照式(6)定義的經驗損失函數,反映模型的擬合效果;待估參數個數取決于p,q,m,n,并且表示為mn2(p+q),反映模型的復雜程度;為實際樣本量.使得AIC或BIC達到最小的p,q取值,將作為QVARDL(p,q)模型的最優滯后階數.

本文給出的信息準則依然沿用了信息準則定義的核心思想,但與傳統的AIC和BIC定義也存在不同之處:1)使用經驗損失而不是對數似然,來表示擬合效果;2)將對數似然前面的負號,調整為經驗損失前面的正號.Yuan[22]和Li等[23]驗證了在分位數回歸框架下AIC準則和BIC準則的定階效果,Monte Carlo模擬結果表明:AIC和BIC準則具有與廣義交叉驗證較為類似的性能,能夠獲得滿意的定階效果.

3 分位數脈沖響應分析

3.1 分位數脈沖響應函數定義

為進一步考察QVARDL模型系統的穩定性,本文通過對隨機誤差項?i,t實施一個沖擊,進而觀察各內生變量以及對應的條件分位數的響應情況,稱其為分位數脈沖響應分析.在QVARDL模型(4)中,為簡化起見,可以不考慮外生變量的影響(取X=Y),僅僅考慮內生變量及其滯后項的影響,從而建立起在QVARDL模型基礎上的脈沖響應分析,可以揭示組成QVARDL系統內生變量間動態影響規律,并描述對隨機誤差項施加一個沖擊后,對內生變量在各個分位點處條件分位數的當期值和未來值所帶來的影響.

定義1第i個時間序列{Yi,t}在第τ分位點處的分位數脈沖響應函數(QIRF)定義如下

其中δ為t時刻的沖擊.在傳統VAR模型及脈沖響應分析中,隨機誤差項?i,t服從對稱分布,一次性沖擊δ常取一個單位的標準差(即δ=1個單位標準差).為簡便起見與滿足可比性要求,本文依然對隨機誤差項?i,t實施一個單位標準差δ的沖擊,來進行分位數脈沖響應分析.

本文給出的分位數脈沖響應函數可以稱為偽分位數脈沖響應函數.這里,t時刻的沖擊δ僅存在于t時刻,其他時刻并不存在沖擊.因此,可以分別給出無沖擊時誤差項的時間路徑為,以及有沖擊時誤差項的時間路徑為.

事實上,本文模型的誤差項可能是更為一般的分布函數,如非對稱Laplace分布,未必滿足對稱性要求.此時,可以考慮一個非標準化沖擊帶來的影響,這一分析在貝葉斯框架下運用貝葉斯分位數回歸,更容易得到相應的分位數脈沖響應分析結果,值得未來進一步研究.

3.2 分位數脈沖響應函數估計

考慮如下數據生成過程,用以描述向量時間序列(Y1t,Y2t)T的動態行為

此外,QVARDL(1,1)模型給出的τ分位點表達式

由此,可以通過矩陣形式來表達t時刻二維向量時間序列的分位數

其中Qt與Yt-1均為二維向量,A和B為2×2的矩陣,矩陣元素如上式所示.

1)一階情形

根據VMA模型設置,t時刻沖擊δ僅僅影響Yt,并不影響.進而可以給出有沖擊時的時間路徑為,此時.

首先,以i=1為例計算分位數脈沖響應函數(QIRF).當s=1時,擾動為常數項,此時只影響,所以有

當s=2時,根據一階VMA模型設置,擾動同時影響Y1,t和Y2,t,有

此時,分位數脈沖響應函數可以表達為

當s≥2時,由于VMA(1)的設置,此時Yt與無關,而對應的條件分位數與有關,有

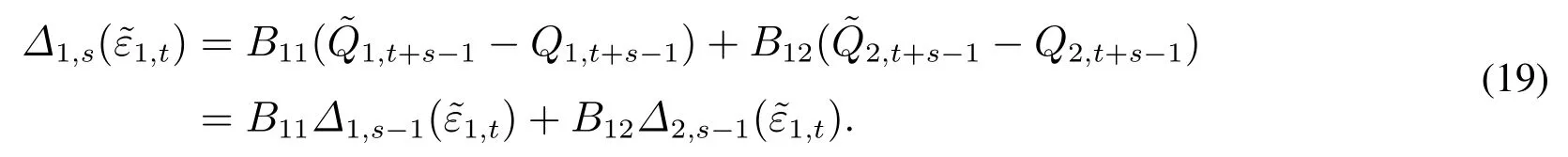
同理,可以得到i=2對應各期分位數脈沖響應函數.當s=1時,有

當s=2時,有

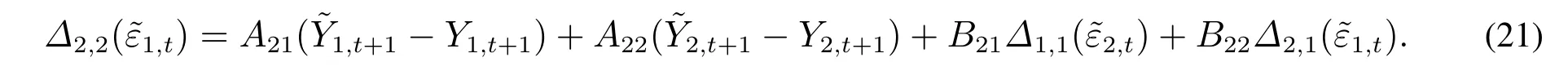
當s≥ 2時,有

由上述推導過程,可以綜合出基于VMA(1)模型的分位數脈沖響應函數一般表達式

2)高階情形

類似地,可以導出高階向量移動平均VMA(k)模型的分位數脈沖響應函數一般表達式(以i=1為例)

當s=1時,同式(19),有分位數脈沖響應函數(QIRF)

當s＞k+1時,由于VMA(k)的設置,無關,僅有對應的條件分位數與有關,即

此時,有分位數脈沖響應函數

由上述推導過程,可以綜合出VMA(k)模型的分位數脈沖響應函數一般表達式

易見,基于VMA(1)模型得出分位數脈沖響應函數正是上式k=1時的特例.至此,本文討論了更為一般情形下的分位數脈沖響應分析,運用高階向量移動平均VMA(k)模型與QVARDL模型之間關系,推導出分位數脈沖相應函數.White等[19]的分位數脈沖響應分析是本文的特例形式,本文是其推廣.

3.3 分位數脈沖響應函數分布特征

分位數脈沖響應函數也是隨機變量,研究其分布特征對于把握其變動規律至關重要.給出如下引理.

引理1Hamilton[24]:對一個向量隨機序列{Zt},若存在,同時有一函數g(·)其在c處有連續的一階導數,則有.

由上述引理,可以得出下列結論.

定理3對于定義1中給出的脈沖響應函數,有

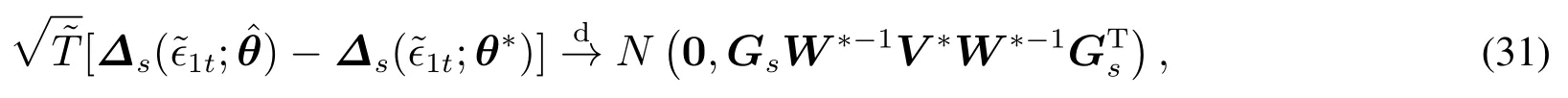
證明定理3的證明過程參見附錄4.

4 實證研究

4.1 數據選擇

楊博理等[25]的研究工作表明,向量自回歸(VAR)模型能夠有效地揭示金融市場之間動態關聯關系.這里,使用本文提出的QVARDL(p,q)模型來檢驗美國次貸危機在世界范圍的影響.在QVARDL模型(4)中,不考慮外生變量的影響,僅僅考慮內生變量滯后項的影響.以美國S&P500指數作為研究基準,同時選取如表1所示的14個不同國家(地區)的綜合指數作為研究對象進行實證研究.樣本數據取2005–01–01至2013–12–31 期間各市場指數日收盤價,其中以2005–01–01至2012–05–31為樣本內,2012–06–01 至2013–12–31為樣本外,樣本數據均來自雅虎財經網站(http://finance.yahoo.com/).這一樣本區間包含了2008年美國次貸危機的完整周期,便于定量研究美國次貸危險產生的影響.收益率采用對數收益率,用自然對數收盤價的一階差分計算rt=100×(lnPt-lnPt-1).

4.2 參數估計

為考察美國次貸危機對其他國家(地區)帶來的影響,以美國市場作為基礎,與其他任意一個市場,分別建立二元QVARDL模型與VMA模型,共建立14個QVARDL模型與14個VMA模型.這里,使用VMA模型描述時間序列的動態變動規律,使用QVARDL模型描述時間序列條件分位數的變動規律.在估計VMA模型與QVARDL模型時,使用2.3節給出的AIC與BIC信息準則,確定了最優滯后階數為VMA(2)與QVARDL(1,1).

表1報告了VMA(2)模型的參數估計結果,為進一步進行脈沖響應分析,定量揭示美國次貸危機沖擊對于不同國家(地區)股票市場的影響,奠定了基礎.表2報告了QVARDL(1,1)模型在一個分位點(τ=0.01,對應99%VaR)處的參數估計結果(限于篇幅,這里略去了其他分位點處的估計結果),可以得到幾個初步結論.第一,在14個QVARDL(1,1)模型中,有超過一半的國家(地區)所得自回歸系數矩陣B中的對角線元素(即B1(11)和B2(12))在統計上顯著(10%水平),意味著條件分位數(與VaR風險對應)過程具有顯著的自相關性.第二,QVARDL(1,1)模型中所有非對角線系數均顯著不等于0,意味著美國與世界其他國家(地區)之間的金融風險存在相互影響.第三,值得注意的是,德國和巴西的自回歸系數矩陣B各元素均在統計上顯著(5%水平).作為歐洲經濟的頂梁柱,德國的出口導向型經濟增長模式以及穩定歐元區經濟狀況的能力在一定程度上對美國造成沖擊;而作為新興經濟體的巴西,以與美國模式不同的經濟政策不斷加強與拉美鄰國、非洲國家乃至印度和中國之間的政治經濟合作,而這正是美國一再鞏固“南北關系”的重要原因.第四,由于考慮到不同國家(地區)金融風險之間相互作用,QVARDL(1,1)模型能夠更加準確預測其金融風險變化規律,結果見圖1和圖2.

表1 14個國家(地區)股票指數與美國的VMA(2)模型估計結果Table 1 Estimated results of 14 countries(districts)from VMA(2)model

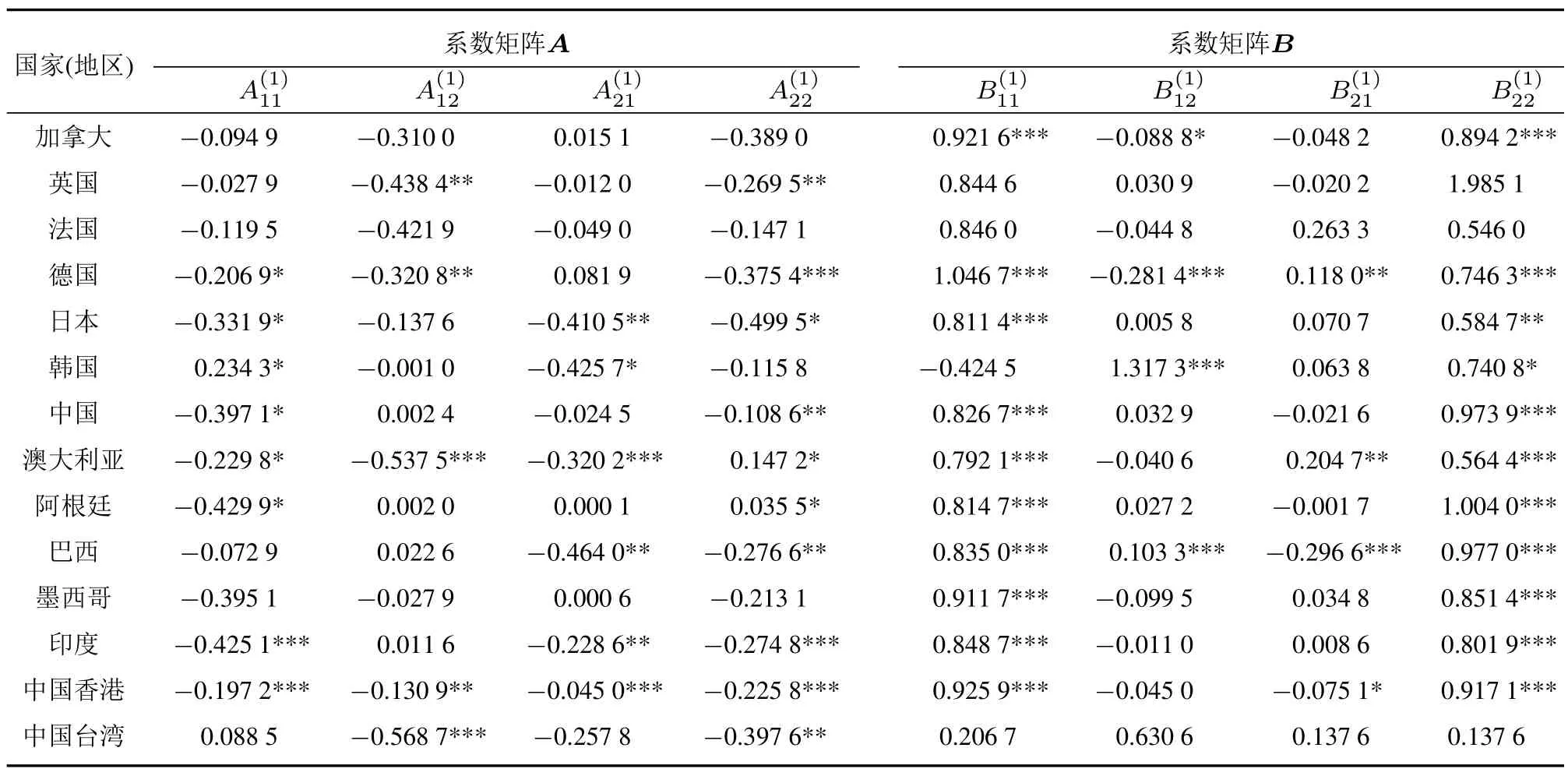
表2 14個國家(地區)股票指數與美國的QVARDL(1,1)模型估計結果(τ=0.01)Table 2 Estimated results of 14 countries(districts)from QVARDL(1,1)model with τ=0.01

圖1給出了15個國家(地區)樣本內的實際收益率(藍線)與99%VaR估計結果(綠線)(限于篇幅,本文略去了其他置信水平VaR估計結果,只報告了極端風險值估計結果),圖2則給出其樣本外預測結果.在圖1與圖2中,美國的VaR是通過在QVARDL(1,1)模型中將兩個內生變量都取做S&P500指數所得,其他國家(地區)的VaR是將模型中的兩個內生變量分別取做S&P500指數及本國(地區)的市場指數.

由圖1可以看出,第一,QVARDL(1,1)模型在樣本內取得了很好擬合效果,表現為99%VaR變動趨勢與收益率變化趨勢吻合程度較高.第二,不同國家(地區)市場均在2007底至2008年初開始出現不同程度波動,并于2008年底至2009年初大幅度波動全面爆發,而這段時間恰逢美國次貸危機集中爆發并演變成全球性金融海嘯.第三,在2011年中下旬不同國家(地區)再次出現不同程度波動,這可能源于歐元區主權債務危機影響.由圖2可以看出,99%VaR同樣與收益率變化趨勢一致,表明QVARDL(1,1)模型同樣具有很好的樣本外表現.

綜合圖1和圖2的信息可知,基于QVARDL(1,1)模型能夠給出準確的VaR風險測度,具有很好的樣本內與樣本外表現.為精確檢驗模型的測算效果,本文采用Kupiec[26]無條件覆蓋似然比(uc.LR)檢驗與Christoffersen等[27]條件覆蓋似然比(cc.LR)檢驗對樣本內與樣本外VaR風險測度進行返回測試檢驗,同時還采用Engle等[14]提出的樣本外動態分位數(DQ)檢驗作為指標檢驗方法,檢驗結果如表3所示.

圖1 15個國家(地區)股票指數的樣本內99%VaR(τ=0.01)Fig.1 Stock indices returns plot for the in-sample days of 15 countries(districts)superimposed by VaR estimates at=1%and 5%

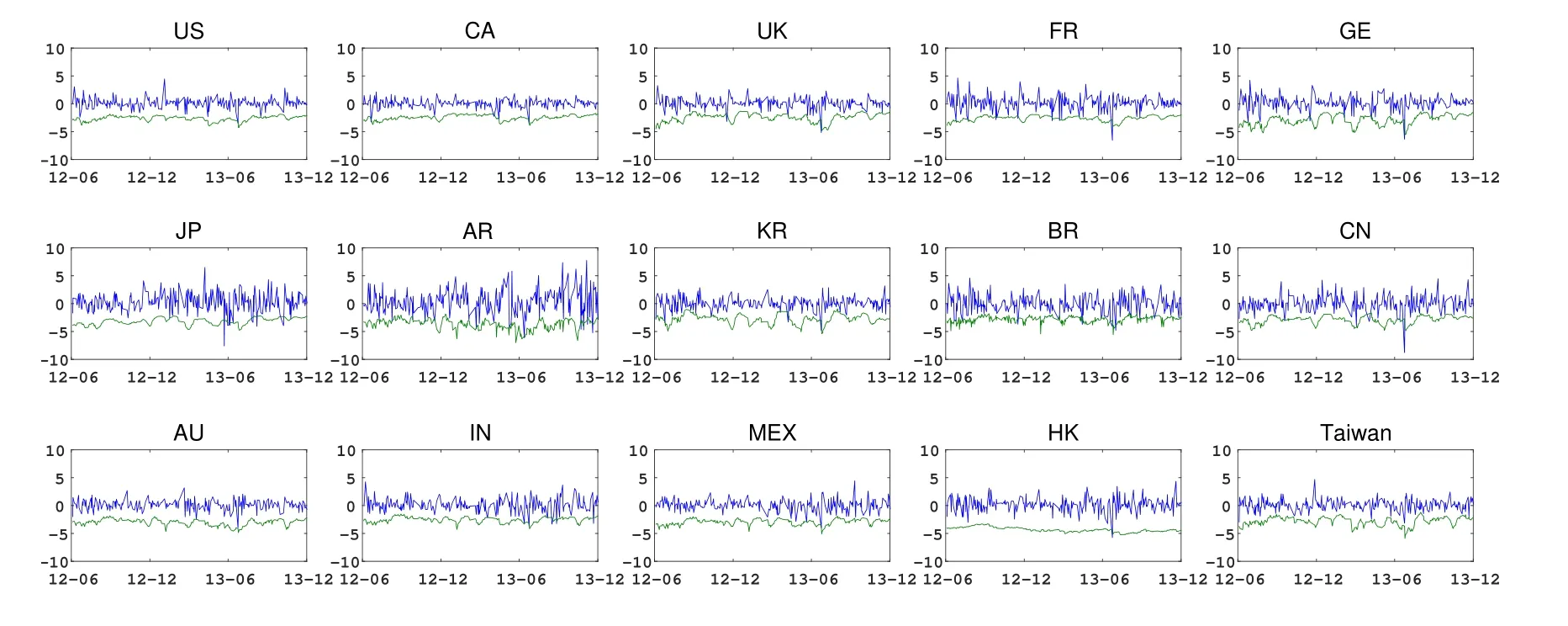
圖2 15個國家(地區)股票指數的樣本外99%VaR(τ=0.01)Fig.2 Stock indices returns plot for the out-of-sample days of 15 countries(districts)superimposed by VaR estimates at=1%and 5%

表3 99%VaR返回測試結果Table 3 Backtesting results of 99%VaR for 14 countries(districts)

續表3Table 3 Continues

由表3,可以得到以下初步結果.第一,除美國以外的14個國家(地區)股票指數的VaR在樣本內均有很好的擬合效果.其中,由uc.LR檢驗可以看出,QVARDL(1,1)模型對日本、韓國與巴西的擬合效果最優,表現為有較大的p值且都為0.987 1;由cc.LR檢驗則可以看出,QVARDL(1,1)模型對韓國與巴西擬合效果最優,表現為p值較大且都為0.867 4.第二,在14個股票指數VaR樣本外預測中,有9個國家(地區)的股票指數通過了樣本外DQ檢驗,僅有阿根廷MERV指數沒有通過cc.LR檢驗;事實上,所有國家(地區)的股票指數均通過了uc.LR檢驗.這一實證結果也表明,在VaR返回測試中,uc.LR檢驗最為寬松,其次為cc.LR檢驗,最嚴格的為DQ檢驗.以上結果表明基于QVARDL(1,1)模型的VaR風險測度在樣本內與樣本外都取得了很好的效果,其中樣本內更為有效,這也與預期結果相符.

4.3 分位數脈沖響應分析

由前面QVARDL(1,1)模型估計結果,已經判定美國金融市場與其他國家(地區)市場之間存在密切聯系.本節主要通過分位數脈沖響應分析,定量揭示不同國家(地區)受美國次貸危機影響的程度與反應速度.黃友珀等[28]認為,有必要研究資產組合收益分位數預測問題.郭華等[29]通過脈沖相應分析考察由特定交易變量構成的脈沖交易對價格波動的沖擊模式.本文中,在一個單位標準差沖擊下的分位數脈沖響應函數可以直觀地報告危機的傳播過程以及危機被吸收(脈沖響應函數收斂于0)的時間,結果見圖3.在圖3中,橫軸代表天數,縱軸表示99%VaR(對應0.01分位數)的變化.

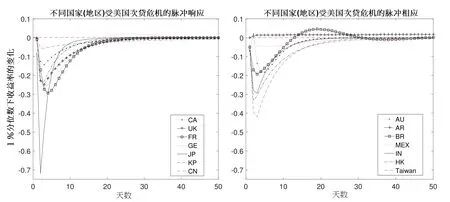
圖3 14個國家(地區)受美國次貸危機影響的脈沖響應(τ=0.01)Fig.3 Impulse response of 14 countries(districts)to the U.S.subprime mortgage crisis(τ=0.01)

由圖3,可以得到如下結果.第一,可以看出大部分國家(地區)在次貸危機爆發后2天～3天內受到了嚴重的沖擊,除了法國與澳大利亞約在5天左右才達到收益率的最低值.第二,歐洲地區包括法國、英國和德國,主要受到次貸危機對本地銀行業的沖擊,受到沖擊后收益率百分比低至-0.2后都開始回升,并在約20天收斂于0值.第三,亞洲地區包括中國大陸、中國香港、中國臺灣、韓國以及日本,其中中國大陸受到次貸危機沖擊影響最小,脈沖響應過程也較短,可以看出美國次貸危機對于中國大陸的沖擊有限,這可能是由于中國大陸準備金充足,所以并沒有造成實質性的影響.中國臺灣地區相對于中國香港地區受沖擊更為嚴重,可能是中國臺灣出口萎縮等原因導致了中國臺灣地區經濟衰退.亞洲其他地區,如日本與韓國對于次貸危機的響應卻有著明顯的差異.日本是受到次貸危機沖擊最大的國家,收益率百分比一度跌破-0.65,這種現象與日本近年經濟發展不穩定有密切的關系,在此期間日本需要面對經濟衰退和通貨膨脹的雙重壓力.第四,墨西哥與阿根廷幾乎沒有受到次貸危機的沖擊,作為拉丁美洲的新興市場,受益于長期以來實施的對外貿易自由化政策,對美國商品市場的依賴性較小,因而受美國次貸危機的沖擊相對有限.

5 結束語

本文提出了一個新的分位數回歸模型:分位數向量自回歸分布滯后(QVARDL),給出其數學表示、參數估計、滯后階數選擇、脈沖響應分析等一整套建模方法.該模型可以同時刻畫多個時間序列在多個分位點處條件分位數之間的關聯關系,能夠整體提升分位數回歸的功能.在結構分析方面,主要通過回歸系數矩陣,定量揭示不同時間序列及其分位數之間的相互依賴關系,有助于解釋經濟系統內部聯系與相互影響.在經濟預測方面,主要通過多變量與自回歸,從橫向與縱向兩個方面把握條件分位數的變動規律,有助于準確預測響應變量在不同分位點處的條件分位數,進而可以準確地進行風險評估.在政策評價方面,主要通過分位數脈沖響應分析,可以考察對經濟系統實施一個沖擊,定量刻畫經濟系統內部的響應情況,評估經濟政策的有效性.

為檢驗提出模型與方法的有效性,本文將其應用于解釋美國次貸危機對世界范圍金融市場產生的影響.實證中,選取世界范圍內主要國家(地區)資本市場作為研究對象,建立QVARDL(p,q)模型并進行分位數脈沖響應分析.通過QVARDL(p,q)模型估計結果發現,一方面,絕大多數國家(地區)的金融風險具有顯著的自相關性;另一方面,美國對世界其他國家(地區)的金融市場存在顯著影響.通過脈沖響應分析發現,美國次貸危機對不同國家(地區)的資本市場在影響程度、影響方式、響應時期等方面有著不同的表現.本文的研究方法與實證結果,為從新的角度研究金融風險及其傳染性提供了一個參考.