PMSM無傳感器模型參考模糊自適應系統*

張相勝， 田佳文， 劉敏杰， 潘 豐

(輕工過程先進控制教育部重點實驗室 江南大學，江蘇 無錫 214122)

0 引 言

傳統的基于模型參考自適應的永磁同步電機(permanent magnet synchronous motors,PMSM)矢量控制系統在轉子的轉速、位置觀測以及參數辨識中都具有較好性能[1,2]。但系統仍然存在強烈依靠觀測器的缺點，當電機參數或者工況發生改變，系統模型也會隨之變化，難以實現最佳性能。文獻[3]提出一種定子電阻觀測器以彌補不足，但該方法會影響系統響應速度。

模糊邏輯算法具有不依賴參數的特點，將其與模型參考自適應系統相結合，能夠從根本上解決傳統算法存在的參數依賴問題[4～7]。文獻[4]提出一種將二階滑膜與模型參考自適應系統(model reference adaptive system,MRAS)相結合的電機轉速測量方法，該方法能有效克服系統中的電流諧波影響，但二階滑膜結構使得系統復雜度提升，運算量加大。相較而言，模糊系統結構簡單，計算量小，文獻[5]提出一種將多狀態統一輸入的模型參考模糊自適應控制方法，該方法實現了降低系統運算量的功能，但其控制器共有七個邏輯子集，模糊蘊涵關系過于復雜，大幅降低了隸屬度函數的校驗成功率。

本文提出一種基于定子電流模型的雙極式模糊邏輯控制系統，利用模糊邏輯單元替換傳統模型參考自適應系統結構中的比例—積分(proportional-intergral,PI)調節器，能夠有效降低系統參數的耦合性，提高轉子轉速跟蹤能力，且優異的自適應能力使其在工況改變時也能有效減小轉速誤差。

1 模型參考自適應系統機理分析

模型參考自適應系統可精確測量定子dq軸電流和轉子轉速，該系統包含參考模型和可調模型兩部分。參考模型用來描述被控對象的已知定量值，可調模型作為模糊自適應機構用于根據給定值產生期望輸出。參考模型的已知定量值與可調模型的期望輸出進行對比，兩者的差值作為誤差信號輸入自適應機制中，再將由此得到的轉子轉速估測值反饋到可調模型。圖1為模糊自適應算法估測轉子轉速的結構框圖。

圖1 模型參考自適應系統結構框圖

設dq軸為PMSM的旋轉坐標系，該坐標系下電機數學模型為

(1)

式中vd和vq分別為定子電壓的d,q軸分量；Rs和Ls分別為定子的電阻值、電感值；ωr,ψr分別為轉子轉速、轉子磁鏈。矩陣形式為

(2)

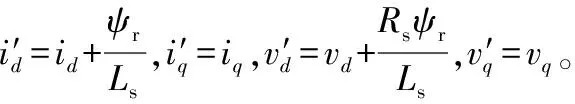
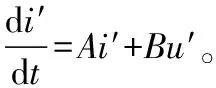
系統可調模型數學方程為

(3)

根據Popov穩定性判據，得出系統串聯模型為

(4)

可知，當D=I時，v=Ie=e。根據Popov超穩定性理論[8]，當系統滿足下面2個條件時，系統具有漸進穩定性：

1)狀態矩陣H(s)=D(sI-A)-1嚴格為正實數；

結合上述分析，得出算法數學模型為

(5)

式中id，iq由參考模型所得，d,q由可調模型根據給定值計算得到。

2 模型參考模糊自適應系統設計

如圖2所示，傳統的模型參考自適應系統參數受系統運行狀態影響。而將其與不依賴參數的模糊控制系統相結合后，新系統響應能力提升，穩態誤差降低。

圖2 2種系統自適應結構框圖對比

模糊系統結構簡單，通過使用模糊控制系統能夠減少算法迭代次數，達到降低計算量的目的。在常用模糊邏輯控制系統中，規則總數隨著輸入參數的增加急劇增長，本文采用一種多級串聯結構，可使系統規則總數線性增長。

本文所提的模糊自適應結構分為2個單元，分析系統各輸入參數相關度，將高相關度變量從第一級單元輸入，低相關度變量從第二級單元中輸入。為了更好地調節系統性能，在每個單元中引入輔助增益系數。雙輸入控制器較傳統單輸入控制器，控制規則更簡單，規則總數也有所減少[5]。

本文所采用的模糊控制系統共含有e1，Δe1，Δe23個輸入變量。根據定義式可知，Δe1是一個關于e1變化的量；Δe2是一個關于e2的變化量

e1=id(k)-d(k),e2=iq(k)-q(k)

(6)

Δe1=e1(k)-e1(k-1),Δe2=e2(k)-e2(k-1)

(7)

表1為根據3輸入變量列出的模糊系統規則表。其中每個輸入變量都有正(P)、負(N)、零(Z)3種狀態。圖3為系統結構，本文采用雙極式的模糊控制系統，每個單元都含有2個輸入變量，第一單元的兩輸入變量分別為e1和Δe1，其輸出變量Δu1及Δe2作為第二單元的輸入變量。

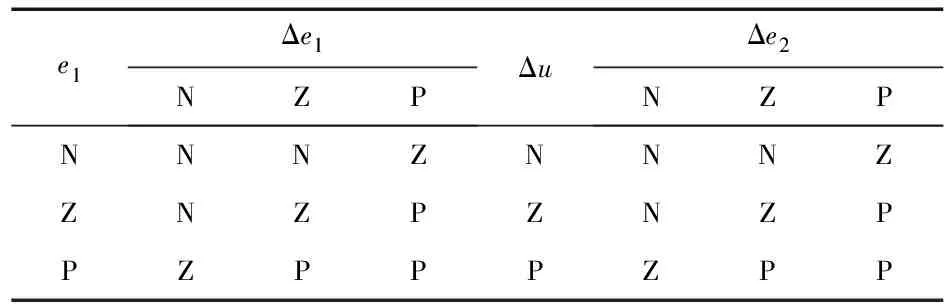
表1 子系統的模糊邏輯規則

圖3 兩級模糊系統結構示意

圖3所示k1～k5分別為對應輸入輸出的輔助增益，目的是為了提升系統性能，其值需根據現場具體工況進行選取。依據系統調試經驗，選擇輔助增益具體數值為k1=k2=k3=k4=1，k5=0.1[7]。

為系統兩個模糊單元選擇隸屬度函數時，由于在設計系統時，將高相關度變量從第一級單元輸入，低相關度變量從第二級單元輸入，可知第一級單元對系統狀態影響更大，其隸屬度函數設計要求也較第二級單元更為嚴格，選取三角形隸屬度函數對系統進行定義，結合系統的邏輯規則表，設計的第一級單元和第二層模糊子系統的隸屬度函數如圖4、圖5所示。

圖4 第一層模糊子系統的錄屬度函數

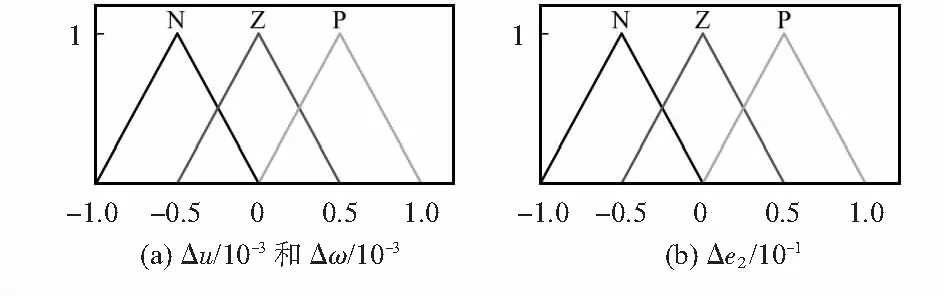
圖5 第二層模糊子系統的錄屬度函數

3 實驗對比與結果分析

在逆變器選用空間矢量脈寬調制(space vector pulse width modulation,SVPWM)調制策略，直流側輸入310 V電壓，開關頻率10 kHz的情況下進行實驗。系統將從電壓、電流傳感器獲取的信號輸入中央處理器(central processing unit,CPU)，根據模型參考模糊自適應算法追蹤轉子轉速。圖6為控制系統的拓撲結構。實驗電機的額定參數為：額定轉速為1 500 r/min，額定功率為500 W，極對數為2，額定電壓為220 V，定子電阻值為3.88 Ω，轉動慣量為0.000 032 kg/m2。

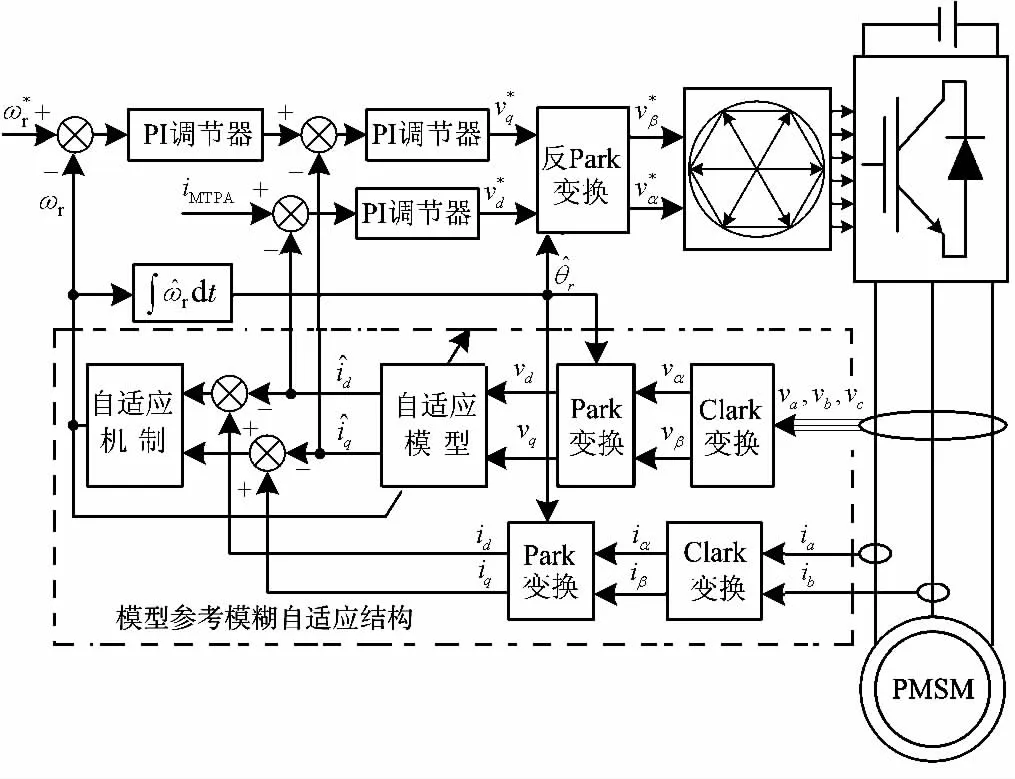
圖6 采用MRAS的PMSM矢量控制系統結構框

3.1 動態性能對比

為了驗證所提算法的動態性能優越性，分別在電機的高、低速域以及不同工況下，采用基于傳統PI調節器的模糊自適應系統和基于雙極式串聯單元的模糊自適應系統進行對比實驗。實驗采用的2種工況如下：

1)電機初始靜止，在0.2 s處給定期望轉速100 r/min，持續0.8 s后，改變給定期望轉速方向；

2)電機初始靜止，在0.2 s處給定期望轉速1 000 r/min，持續0.8 s后，改變給定期望轉速方向。

圖7給出了在低速和高速不同工況下分別采用2種算法的實驗所得波形。可知，在低速工況本文算法動態響應性能更優，響應時間約降為傳統方式的30 %。在高速工況下本文算法在動態響應方面仍然具有顯著優勢，響應時間約為傳統算法的60 %。另外，由于模糊控制的固有屬性，其在穩態運行時的紋波和轉速誤差也較傳統PI算法更好。

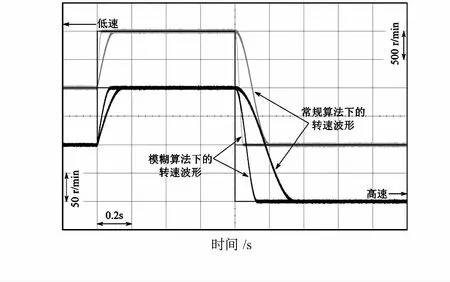
圖7 低速和高速不同工況下2種控制算法的轉速實驗波形

一般，模型參考自適應系統在電機高速域內對轉子位置的測量更為準確，在低速域內，測量則精度大大降低。

圖8為在低速工況下采用2種算法的轉子位置估測結果。可知，采用模型參考模糊自適應算法的系統在轉子位置估測時用時更短，精度更高(估測精度約提升57 %)。

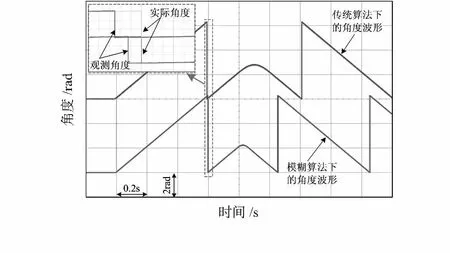
圖8 低速工況下2種控制算法的位置估算結果

3.2 穩態性能對比

為了驗證本文所提算法在穩態運行時的優越性，在電機低速(100 r/min)、中速(500 r/min)、高速(1 000 r/min)下進行實驗，實驗結果如表2所示。分析可知，在不同轉速域時，本文算法的各項穩態指標性能均有所上升，優化效果明顯。

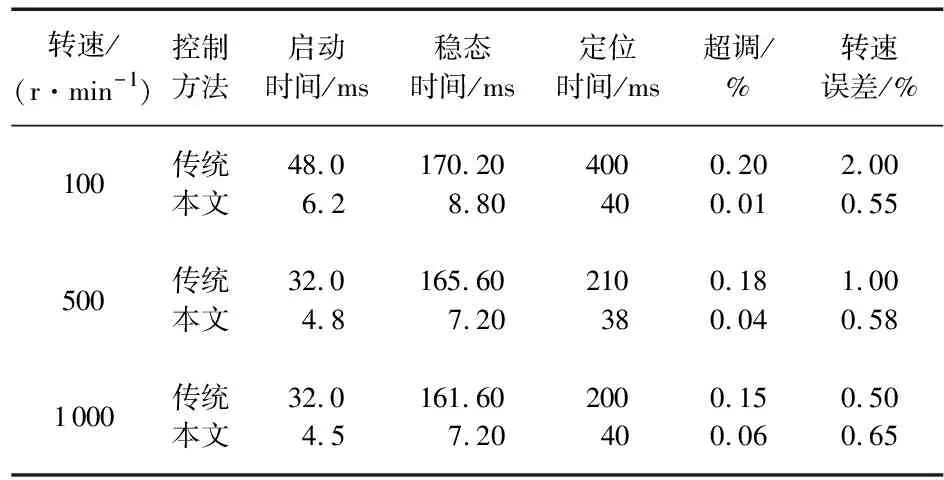
表2 2種不同轉速下各項穩態性能指標對比

4 結 論

針對傳統PMSM模型參考自適應系統的不足，本文提出一種基于模糊控制算法的新型PMSM自適應系統。實驗結果表明，與基于PI調節器的算法相比，所提算法能夠有效降低系統計算量，減少系統響應時間，改善系統的動、穩態性能，且能彌補傳統算法在低速域下轉速誤差大、跟蹤時間長的不足。另外，該算法結構簡單，適合廣泛應用在數字系統中。