基于鴿群優化改進的粒子濾波算法*

韓 錕, 張 赫

(中南大學 交通運輸工程學院, 湖南 長沙 410075)

0 引 言

粒子濾波(particle filtering,PF)通過非參數化蒙特卡洛方法實現遞推貝葉斯濾波[1],擺脫了傳統解決非線性濾波問題時,隨機量必須滿足高斯分布的制約條件[2],使其能夠在無線定位、金融與經濟學、參數估計、目標跟蹤[3～5]等非線性系統下,展現出明顯的優越性。然而,傳統的PF在重要性采樣后會出現粒子退化問題,通過重采樣[6]后又會導致粒子貧化現象[7]。而且狀態預測過程中往往需要大量粒子,這會使得計算效率低下[8]。為了解決上述問題,Li T等人[9]提出確定性重采樣,張光等人[10]采用正則化方法,羅穎等人[11]提出智能采樣,均有效緩解粒子退化問題,但無法從根本上解決粒子貧化問題。

將群體智能優化算法與PF結合是目前PF發展的一個較新的思路[12],主要是將粒子看作生物群體的個體,通過模擬生物集群的運動規律調整粒子的分布,由于其過程并未舍棄權重低的粒子,能夠從根本上避免粒子貧化現象[13]。目前,已先后有將遺傳算法、粒子群算法、人工魚群算法、螢火蟲算法等智能優化算法與PF結合的實例[13～16]。本文結合最新的鴿群優化(pigeon-inspired optimization,PIO)算法[17,18]以及PF[19]的特點,對鴿群優化2種算子加以改進,并引入自適應交叉操作,保障粒子多樣性。通過模型仿真實驗表明本文所提算法在保證粒子多樣性的同時能夠很好地提高狀態估計精度與穩定性。

1 PIO算法

PIO算法基本流程主要由以下兩種算子分別進行的迭代循環組成[18]：

1)地圖和指南針算子(map and compass operator)：在搜索空間隨機初始化種群數量為N的鴿群,每只鴿子的位置和速度依據式(1)進行迭代更新

(1)

式中xgbest為當前全局最有位置,R為地圖與指南針因子,t為當前迭代次數。

2)地標算子(landmark operator)：每次迭代循環中,適應度較低的那一半鴿子被剔除。余下的鴿子以其中心位置作為導航繼續飛行,設fitness(x)是鴿群適應度函數,位置更新公式為

(2)

(3)

2 基于PIO算法的PF

標準PF過程中,經過重要性采樣得到N個粒子后,此時利用PIO算法,對粒子群體進行兩種算子運算,使粒子不斷向高似然區域靠近。然而PIO算法存在著極易陷入局部最優的問題,需要對鴿群優化過程進行適當修正與改進。

2.1 速度更新改進策略

由PIO算法流程可以發現PIO算法與粒子群算法有相似之處,兩者都遵循以下規則：向目的地運動和向群體的中心運動[20]。但2種算法也存在著明顯的不同,粒子群算法每次迭代都是用速度慣性、粒子本身最優值以及種群最優值一起決定下一位置。鴿群算法中速度的更新主要依賴于指南針因子、迭代次數以及當前全局最優值等。針對不同問題,兩種算法結果會不同。因而本文聯合兩種更新公式,設計鴿群速度更新為

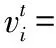
(4)

通過調節α和β的值,充分利用兩者速度各自更新優勢。

2.2 地標算子改進策略

PF最終狀態輸出依賴的是所有粒子的位置,將PIO算法與PF結合時不能舍棄低權重的粒子,這同時也保障了粒子多樣性。本文改進地標算子策略如下：每次迭代循環中,首先對種群的適應度進行排序,適應度較高的那一半鴿子,以其中心位置作為當前所有鴿子的導航地標,鴿群向該位置飛去,然后再隨機飛出繼續搜索,如此循環直到達到最大迭代次數或是設定的精度為止。改進后地標算子為

(5)

式中 (2rand-1)為[-1,1]間的一個隨機數,表示個體搜索的隨機方向;h為最大搜索半徑。

2.3 自適應交叉因子

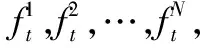
(6)

式中pc1與pc2為交叉概率的變化范圍,fb為兩個交叉個體中較大的適應度值,fmax為種群中最大適應度值,favg為種群適應度平均值。可以使得適應度值接近最優的那部分個體也可以保持一定的交叉概率,這部分個體經過交叉運算以后,可增加新產生的子代個體中優秀個體的數量。

3 算法設計

本文將最新量測值引入采樣過程,定義適應度函數為

(7)

式中ηk為測量噪聲方差,zk為最新觀測值,zpre(i)為觀測預測值。

算法流程如下：

1)初始化參數：粒子數N,2種算子最大迭代次數T1max,T2max,最大速度vmax,地圖與指南針因子R,學習因子c1,c2,α,β的值以及自適應交叉概率范圍。

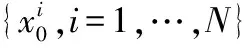
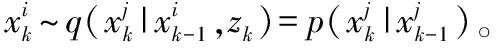
4)根據式(7)計算每個粒子適應度值,并找出當前全局最優值位置。

5)給予N個粒子隨機的速度Vi,以xi作為個體歷史最優位置,適應度值作為各自歷史最優值pbest,并找出粒子中最大適應度值以及對應坐標gbest。對種群分布進行鴿群優化。

地圖和指南針算子優化：

1)根據式(4)、式(1)更新每個粒子的速度和位置,重新計算適應度值。

2)由式(6)確定2個隨機粒子的交叉概率,隨后進行交叉操作。

3)重新計算適應度值,更新pbest和gbest。

4)判斷迭代是否達到最大次數T1max,若是,則結束循環;否則,繼續步驟(1)。

地標算子優化：

1)將粒子的適應度值進行排序,取適應度值較大的一半鴿子的中心作為導航地標。

“現在，我等對于但采氏有兩法：一、彼若于二月底回國，則月薪送至二月止。二、若彼仍繼續工作(無論在寧在平)，則按月送薪，至彼歸國之月止。至于暫領生活費辦法，由于我等愛國愛院的熱心；彼是外國人，不便以愛中國之心責之；彼在本院，時期雖短，即將解約，亦不便以愛院之心責之。彼抱一片熱心而來，不意因水土不服，夫婦均大病，幾喪其生命。物質精神上之損失已不少，稍加優待，當能為諸同事所諒解。”[11]22

2)所有鴿子飛向中心位置,再按照式(5)隨機飛出,重新計算適應度值。

3)根據式(6)確定2個隨機粒子的交叉概率,隨后進行交叉操作。

4)重新計算權值,找出適應度值較大的一半鴿子的中心位置。

5)判斷迭代是否達到最大次數T2max,若是,則結束循環;否則,回到步驟(2)。

4 模型仿真實驗

為了驗證本文算法的有效性,對比了標準PF、遺傳算法優化PF(genetic algorithm-PF,GA-PF)、粒子群優化PF(particle swarm optimization-PF,PSO-PF)以及鴿群優化粒子濾波(PIO-PF)在粒子總數為50和100時的濾波仿真實驗。采用單變量非靜態增長模型作為仿真對象,模型為

(8)

式中wk和vk皆為零均值高斯噪聲,設系統噪聲wk方差Q=1,測量噪聲vk方差R=1,迭代次數T為50,GA-PF中交叉概率為0.7,變異概率為0.05。

取均方根誤差(root-mean-square error,RMSE)作為算法估計精度的判定值,RMSE公式為

(9)

以RMSE的方差作為算法的穩定性判定依據,方差越低,表明算法穩定性越好。圖1為4種算法粒子數N=100時,獨立運行100次RMSE仿真結果,以及算法分別在不同粒子數下100次獨立實驗的RMSE值。

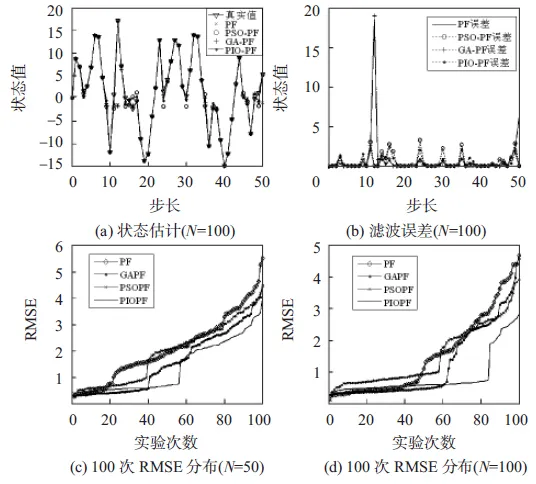
圖1 仿真對比結果

與標準PF,GA-PF以及PSO-PF相比,本文所提PIO-PF算法狀態預測曲線與實際狀態相似程度最高。而圖1(c)和圖1(d)中PIO-PF無論在粒子數為50或是100時,RMSE曲線均最低,表明PIO-PF算法要優于其他3種算法。表1中數據為每種算法獨立運行100次后的均方跟誤差平均值以及方差,從中可以看出,PIO-PF的均方根誤差以及方差最低,且在粒子數為100時兩者皆小于1,當粒子數為50時,其誤差值也比粒子數為100的PF以及PSO-PF算法低,與GA-PF也只有0.01左右的差距,說明PIO-PF能夠用較少的粒子達到所需的精度。而均方根誤差方差體現算法預測的穩定性,PIO-PF也是最低的,當粒子數越多時更為明顯。

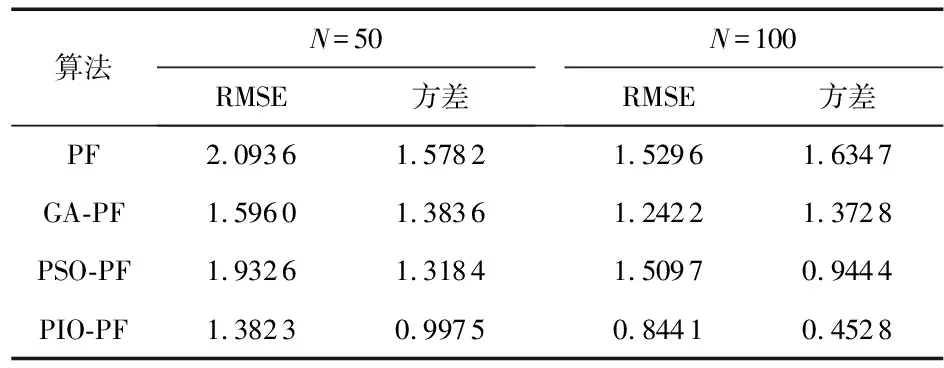
表1 實驗結果

5 結 論

本文將PIO算法應用到PF中,驅動粒子不斷向高似然區域移動,更加接近真實分布。在單變量非靜態增長模型仿真實驗中,粒子數為100時,PIO-PF實驗結果均方根誤差均值為0.844 1,RMSE方差為0.452 8,算法精度、穩定性均高于同類其它算法。相對于標準PF,本文所提算法精度提高了45 %,穩定性提高了72 %,且濾波過程所需粒子數也大幅減少。