一道數學錯題里的思維奔流

文 李保偉（浙江麗水市文元集團文元小學）

一次，我布置的家庭作業中有一道這樣的題：求以5為軸的旋轉體的體積。如下圖：

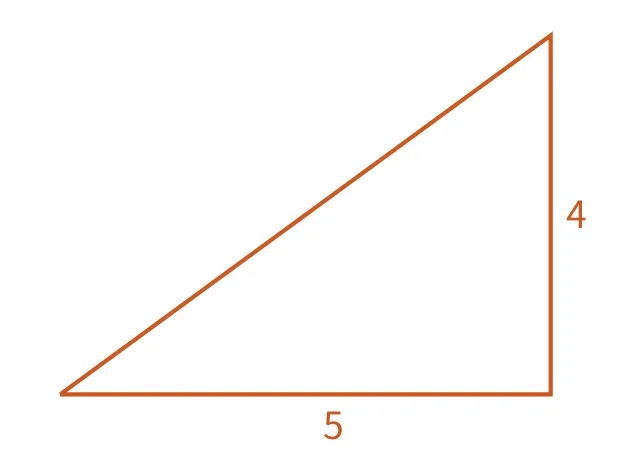
這道題應該在孩子們的知識范圍內，但沒想到在批改作業時還是發現有一小部分孩子做錯了。孩子們錯誤的原因并不是不懂得怎么求體積，而是誤讀了題目，沒能很好地理解“以5為軸”。他們受圖的影響，條件反射地將“5”當成旋轉體（圓錐）的半徑來計算了。

為此，我便就這道題進行了評講。通過操作演示，讓學生理解“以5為軸”表示“5”是旋轉體的高，“4”是旋轉體的底面半徑。

孩子都理解后，我隨機拋出了一個問題：那些做錯了的同學所列的式子其實是表示以誰為軸的旋轉體體積？孩子們馬上明白了，這個直角三角形既可以“5”為軸旋轉，也可以以“4”為軸旋轉，從而得到不同的旋轉體（圓錐）。

“老師，可否以這個直角三角形的斜邊為軸旋轉？”一向思維敏捷的梓洋提出了自己的新思考。

我心中一陣竊喜，順勢說道：“如果以這個直角三角形的斜邊為軸旋轉一周后的旋轉體是怎樣的呢？請同學們和同桌討論一下，并畫出來哦。”

當孩子畫出了這個旋轉體的幾何圖后，大家紛紛在思考如何求它的體積。孩子發現這個旋轉體其實是由兩個等底但不等高的大小不一的圓錐組成的。而要求圓錐的體積，需要知道高和底面半徑等條件。可是，這些直接的條件好像都沒有。

在靜靜地思考與等待中，有個參加過思維輔導班的孩子說，要先求出這個直角三角形的斜線，需要用到勾股定理。這時，我又順勢說這是個不錯的建議，但直角邊用“4”和“5”似乎不妥，干脆改為“3”和“4”，這樣就清楚地知道了斜邊應該是“5”。如下圖：

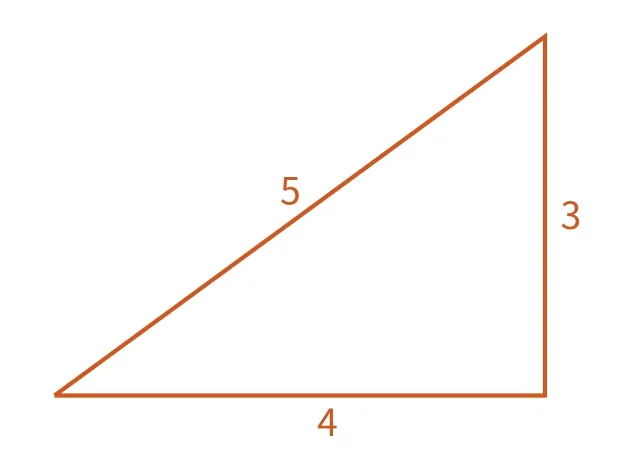
根據三角形已有的條件又可以求出斜邊5所對應的高是2.4，而2.4同時也是旋轉體的半徑。如下圖：

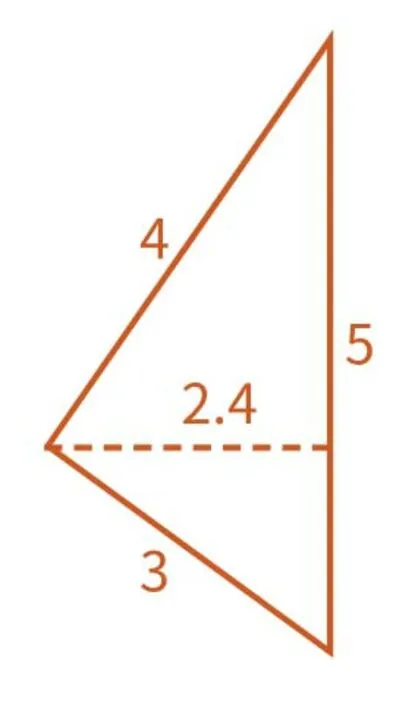
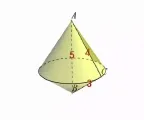
孩子們通過畫圖發現：2.4同時也是旋轉體的半徑（也就是上下兩個圓錐體共同的半徑）。現在半徑知道了是2.4，可上下兩個圓錐各自的高還不知道，還好我們知道兩個圓錐高的和是5。

在靜靜地思索中，有個孩子提出了自己的解題思路：先假設兩個圓錐的高分別為h1、h2，并列式如下：

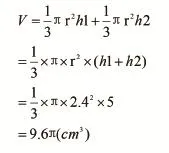
這個式子一出來，孩子們恍然大悟，這樣的兩個等底不同高的圓錐組合體體積其實就是底面積×兩個圓錐的高之和×1/3，也就是說還可以把這組合體轉化成高為5、底面半徑為2.4的圓錐。

于是，大家便很快地列出了新的算式：

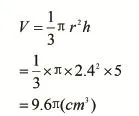
既然可以將兩個等底的圓錐的高看成一個圓錐的高之和，那么如果求兩個等底等高的圓錐和圓柱組合體，我們可否從多個角度去看去用多種方法求呢？

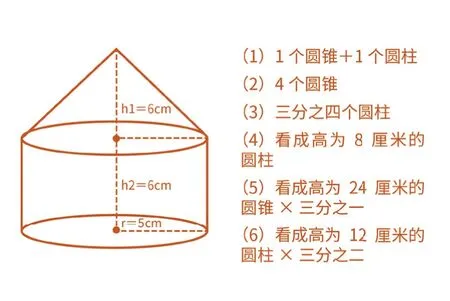
這道題至此也就告一段落了。

風起山東，演繹美

應北京師范大學老教授協會之邀，我去山東淄博參加了“中國教育夢——思維導圖融入學科教學實踐分享會”，并在活動中執教一節思維導圖應用于數學教學的示范課。

當時我報給主辦方的是一節六年級的分數復習課“五分之四的聯想”，之前在全國各地上過幾次，反響還是不錯的。只是到活動前兩天，我才了解到淄博使用的青島版教材是“五四”制的，小學只有五年級，我之前報的課題是六年級的內容——這就意味著我必須換課題了。

可時間這么緊迫，怎么辦？這時我萌發了把“直角三角形”的“轉”這道題用思維導圖串起來設計成一節課去試試的想法。于是，再次修改之前的“思維導圖”。這次調整把原來設想的“直角三角形”的“移”改為了思考兩塊“直角三角形”怎么“旋轉”的問題。由于忙著制作教具和課件，再說學校的六年級只有自己教的兩個班，所以重新調整后的設計也沒有去試教。從某種意義上說，在山東淄博，我上的這節課是一節“裸課”。

我就是按這幅重新設計的思維導圖的結構圓滿完成了整節課的教學。現場的聽課老師反響很大，紛紛說：沒想到課還可以這么設計這么上。而這一切都是虧了“思維導圖”這種結構化、發散性的思維工具。

不斷挖掘，創造美

山東上完課回校后，我不斷在沉思著：這節課只能這樣設計嗎？本課后半段設計有沒有更好的調整策略？

當與同事辛鋒老師交流時，他一語給了我靈感：可不可以思考繞某個頂點水平旋轉一周？

真好！于是，我帶著這樣的思路來檢驗孩子們，沒想到兩個班的孩子在我的啟發下很快就想到了這種旋轉方式，不但迅速畫出了分別繞頂點A、B、C的三種旋轉體的幾何圖，而且還知道計算出他們體積的思路。

于是，我和孩子再一次回顧新的設計，發現是從“沿邊旋轉”和“繞點旋轉”兩種情況來思考三角形的旋轉體的。于是便將原來只是考慮“沿邊旋轉”的三條分支概括為“沿邊轉”，去掉了“兩個直角三角形”的旋轉情況，加入“繞點旋轉”的三種情況。于是，整個設計調整為“沿邊轉”和“繞點轉”這兩條大分支。

這樣的設計把一個“直角三角形”的旋轉挖掘得更加充分了。正當我和孩子們“思”得其樂、樂在“思”中時，一個孩子提出了他的想法：既然直角三角形可以用“轉”形成這么多種旋轉體，那長方形、正方形等平面圖形可不可以用“轉”得到旋轉體呢？于是，我們又開始了“轉”的思維導圖研究。且看孩子們的作品吧。

這個孩子想到長方形、直角三角形、直角梯形、正方形的不同旋轉所得到的旋轉體。見下圖：

這又是兩個學霸級人物，自主按“三角形”“直角梯形”“四邊形（再分平行四邊形、長方形、正方形）”“圓”來進行不同情況的旋轉想象，不僅能畫出幾何圖，還能嘗試計算。見下圖：

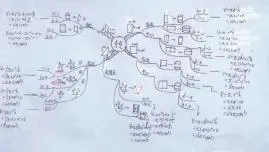
“轉”出門道，放飛美

想象力沒有天花板，這個孩子的空間想象力已經完成超越了小學的水平了。見下圖：

當孩子們用“轉”為主題的思維導圖來概括有關圓柱和圓錐的知識后，似乎著了魔似的。六（2）班的孩子紛紛問我：李老師，還有什么主題的思維導圖可以畫？我反問他們一句：你們覺得呢？那就以“切”為主題畫一幅有關圓柱圓錐的思維導圖吧。見下圖：

當孩子們把思維導圖交上來，我進行點評時，有些孩子的思維又一次被拔節，覺得可以把“削”也融入“切”進去。我靈機一動：如果要考慮切和削，這都和什么有關？都和“刀”有關。所以，在六（1）班，我們便改成以“刀”為主題的思維導圖了。見下圖：

通過一系列的推演和深化，當初家庭作業中的一個小小的誤讀，演化出無限的數學之美。對于我來說，培養孩子們獨立思考和邏輯推演的能力，遠勝過單純傳授一個知識點。數學之美，美在邏輯、美在系統化、美在思考、美在理性。很高興孩子在這么小就能通過這樣一個小小的課題去探索無限的數學之美。

在這個過程中，思維導圖是一個有效思維圖形工具，運用圖文并重的技巧，開啟大腦的無限潛能。思維導圖以放射性思考模式為基礎的收放自如方式，除了提供一個正確而快速的學習方法與工具外，還可以成倍地提高學習知識速度和效率，幫助孩子們更快地學習新知識與復習整合舊知識。希望孩子們在今后的學習中，也可以維持這樣的探索精神，勇敢地去探索數學的形與美。