思維導(dǎo)圖在高中數(shù)學(xué)學(xué)習(xí)中的研究

孫擎龍

（菏澤一中，山東 菏澤）

高中生在高中數(shù)學(xué)學(xué)習(xí)階段，是應(yīng)用思維導(dǎo)圖，形成數(shù)學(xué)品質(zhì)的最佳時期，因此，研究思維導(dǎo)圖在高中數(shù)學(xué)學(xué)習(xí)中的應(yīng)用，不但有利于高中生更好地學(xué)習(xí)數(shù)學(xué)，更為未來的人生道路打下堅實的基礎(chǔ)。

一、高中數(shù)學(xué)知識的特性

1.知識量廣闊

高中數(shù)學(xué)相對于初中數(shù)學(xué)而言實現(xiàn)了量的劇增。隨著知識點的與日俱增，知識點之間的聯(lián)系性更加緊密、邏輯性更加嚴(yán)整。高中數(shù)學(xué)知識量的傳遞主要通過教師和教材以及課后大量習(xí)題來鞏固。

2.數(shù)學(xué)語言更加抽象

高中數(shù)學(xué)更多的是符號語言、邏輯運算語言、函數(shù)語言、圖形語言等，脫離了初中數(shù)學(xué)形象思維的土壤，以更加抽象的形式將物質(zhì)抽象，從而要求學(xué)生具備更強的邏輯思維能力。

3.高中數(shù)學(xué)知識點銜接性更強

高中數(shù)學(xué)知識點銜接緊湊表現(xiàn)在教材中顯示出層層遞進(jìn)的關(guān)系，且呈螺旋式上升。知識點分布于各個章節(jié)，縱橫交錯，形成了點、線、面、網(wǎng)的系統(tǒng)性數(shù)學(xué)知識結(jié)構(gòu)。比如，高一數(shù)學(xué)必修一，第一章學(xué)習(xí)集合，第二章學(xué)習(xí)函數(shù)。函數(shù)的定義域和值域反過來用到集合的概念，銜接性極強。

二、高中數(shù)學(xué)課程學(xué)習(xí)特點

通過上述三點的闡述，我們發(fā)現(xiàn)：高中數(shù)學(xué)知識的特性不但適合引入思維導(dǎo)圖，同時依據(jù)高中生邏輯思維能力也說明了思維導(dǎo)圖引入的可行性。因此，我們針對高中數(shù)學(xué)課程學(xué)習(xí)特點進(jìn)行進(jìn)一步分析。

1.數(shù)學(xué)學(xué)習(xí)的推理性

初中數(shù)學(xué)向高中數(shù)學(xué)轉(zhuǎn)變的最顯著特征是：學(xué)生由“想學(xué)”必須轉(zhuǎn)變?yōu)椤皶W(xué)”。因此，高中數(shù)學(xué)知識間的聯(lián)系性，迫使高中生必須具備思維的預(yù)見性。學(xué)生學(xué)習(xí)方法的最大變化表現(xiàn)為探究式學(xué)習(xí)方式的轉(zhuǎn)變。高中生要學(xué)好數(shù)學(xué)必須敞開思維，通過猜想與假設(shè)的手段，發(fā)現(xiàn)知識間的規(guī)律，通過習(xí)題的實例證明猜想的正確性。因此，高中數(shù)學(xué)思維上的推理性特征極為顯著。

2.數(shù)學(xué)學(xué)習(xí)的辯證性

具備了推理性，并不意味著每一次猜想與假設(shè)都正確。必須從大膽猜想、小心求證的科學(xué)態(tài)度入手，用辯證的眼光看待數(shù)學(xué)邏輯上的辯證與論證。從特殊到一般，從整體到個體，只有掌握辯證性思維才能最終獲得正確結(jié)論。

3.數(shù)學(xué)學(xué)習(xí)的完整性

高中數(shù)學(xué)學(xué)習(xí)的循序漸進(jìn)特性，需要逐步將已學(xué)的知識和新知識形成“點—線—面—網(wǎng)”的擴充路徑。因此，整個高中三年是數(shù)學(xué)學(xué)習(xí)的整體性過程，最終形成完整的數(shù)學(xué)知識框架認(rèn)知。

4.數(shù)學(xué)學(xué)習(xí)的發(fā)散性和創(chuàng)造性

高中階段的學(xué)生無論是心理還是生理，都像海綿一樣孜孜不倦地吸收著各種營養(yǎng)。因此，數(shù)學(xué)學(xué)習(xí)中對新世界的發(fā)現(xiàn)過程，是提升高中生數(shù)學(xué)學(xué)習(xí)興趣的關(guān)鍵。此時鼓勵高中生主動進(jìn)行發(fā)散性思維的訓(xùn)練，創(chuàng)造性的嘗試，有利于高中生對于數(shù)學(xué)體系的整體性把握。

三、思維導(dǎo)圖在高中數(shù)學(xué)學(xué)習(xí)中的應(yīng)用

1.高中數(shù)學(xué)學(xué)習(xí)引入思維導(dǎo)圖的必要性

從以上高中數(shù)學(xué)知識的特性和數(shù)學(xué)知識學(xué)習(xí)特性來看，通過思維導(dǎo)圖的構(gòu)建，能夠很自然地形成以核心知識點為關(guān)鍵詞的知識結(jié)構(gòu)。通過關(guān)鍵詞之間的連線，能夠?qū)D、文、色彩組合而成的思維導(dǎo)圖聯(lián)系成完整的高中數(shù)學(xué)知識體系。

2.基于思維導(dǎo)圖的高中數(shù)學(xué)學(xué)習(xí)案例分析

思維導(dǎo)圖從學(xué)生組織、實施、檢驗開始，就已經(jīng)引導(dǎo)學(xué)生進(jìn)行數(shù)學(xué)知識的構(gòu)建和整合。也是將高中生理解和接受知識的過程進(jìn)行動態(tài)展示的表現(xiàn)。下圖是針對《空間立體結(jié)合初步》一章給出的思維導(dǎo)圖設(shè)計，如下圖所示：

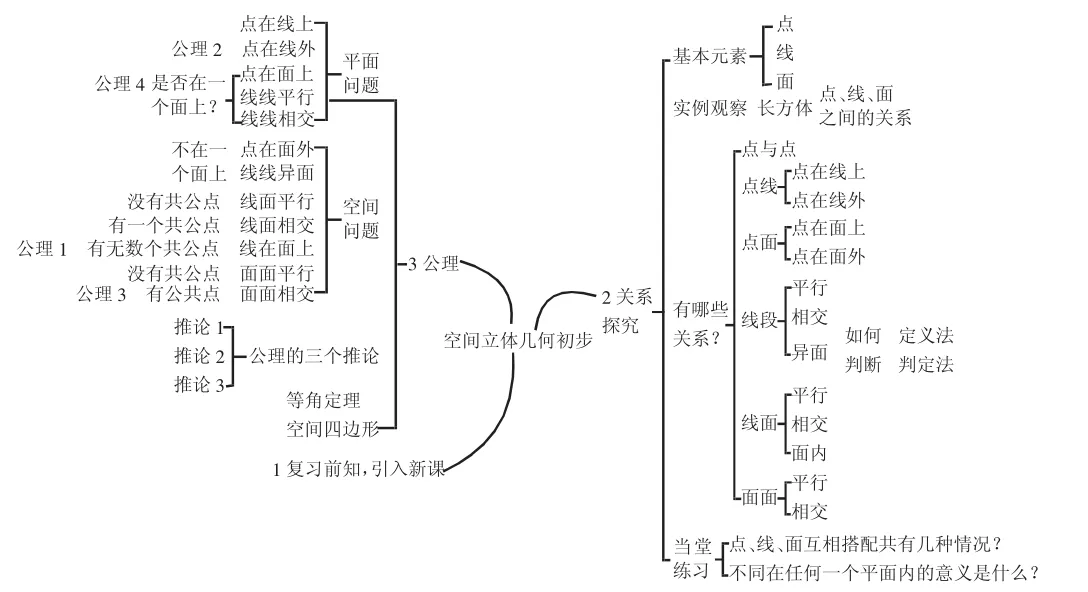
空間立體幾何初步學(xué)習(xí)思維導(dǎo)圖

上圖中明確給出《空間立體幾何初步》一章的學(xué)習(xí)方法、步驟以及具體實現(xiàn)目標(biāo)。整體而言，針對一章的學(xué)習(xí)要實現(xiàn)“預(yù)習(xí)—關(guān)系探究—公理探析”的遞進(jìn)步驟。復(fù)習(xí)和預(yù)習(xí)階段是為后期學(xué)習(xí)的思辨論證奠定基礎(chǔ)；關(guān)系探究是直觀感知本章知識要點的動態(tài)過程；公理探析則為操作和度量計算做鋪墊。借助于思維導(dǎo)圖進(jìn)一步將學(xué)習(xí)策略細(xì)分后，形成如下路徑：

關(guān)系探究過程，需要理論聯(lián)系實際，從基本元素入手進(jìn)行實例觀察，通過觀察結(jié)合教材闡釋空間立體幾何各項關(guān)系，并要在課堂中實現(xiàn)基本元素及其關(guān)系的認(rèn)識和理解。

公理探析階段關(guān)鍵要實現(xiàn)從具體到抽象的演化過程。通過上一步知識點與線的連接，形成公理探析過程中數(shù)學(xué)知識面的認(rèn)識和理解。從特殊到一般，具體到抽象，并能夠借助于數(shù)學(xué)語言描述一般情況下上圖中點、線、面各個知識點的位置關(guān)系，逐步將簡單旋轉(zhuǎn)體和多面體的形象思維抽象成基本元素的數(shù)學(xué)語言，并掌握其相關(guān)概念和公理。

綜上所述，思維導(dǎo)圖不是簡單的關(guān)鍵詞堆砌，而是不同的思維條件、學(xué)習(xí)方法下產(chǎn)生的包羅萬象的大腦數(shù)學(xué)思維模式的形象體現(xiàn)。因此，高中生在制作思維導(dǎo)圖時切忌貪多或大而全。需要從當(dāng)前所學(xué)知識入手，形成在一張思維導(dǎo)圖中呈現(xiàn)知識點、問題以及自身所學(xué)薄弱部分等分支。