例談對數學歸納法局限性的認識誤區

朱 榮

（甘肅省康樂一中，甘肅 臨夏州）

數學歸納法是證明與正整數有關的數學命題的一種重要方法，在各級各類考試中有廣泛應用。使用數學歸納法證題必須要有兩個步驟，一是作為歸納的基礎，二是歸納遞推，即對某些與正整數有關的命題常采用下面的方法來證明它們的正確性：①當n取第一個值n0時，命題成立；②假設當n=k（k∈N*且k≥n0）時命題成立，證明當n=k+1時，命題也成立，這種方法叫做數學歸納法。用數學歸納法證明一個命題的基本結構是“兩個步驟，一個結論”。這種方法粗看起來好像是一種萬能的，只要是與正整數有關的命題都能證明，但實際操作起來并非易事，學生經常犯以下錯誤，有的不重視第一步的驗證，有的對n的第一個值不仔細研究誤認為是1；有的只是形式上用數學歸納法進行了照葫蘆畫瓢式的書寫，其實由于沒有使用歸納假設或根本不會變形使用歸納假設，而繞開最關鍵的步驟，致使形式上好像進行了證明，其實并沒有證明，造成錯誤，因此，證明時①和②這兩個步驟缺一不可，步驟①是步驟②的基礎，步驟②是遞推的依據。關鍵是第二步：怎樣由假設n=k成立，推證出n=k+1時，命題成立，以及如何根據題目條件，再創造條件，巧妙使用歸納假設是證明的難點。

數學歸納法雖然自有其局限性，但學生往往由于對以上情況的理解不透，把握不準，功力不夠，使用不當，在應用數學歸納法時常常感覺數學歸納法好像很容易但又常常出錯，有時又覺得對有些與正整數有關的題目數學歸納法是失效的，而陷入迷茫，甚至感到走入絕境而不知所措的誤區，致使對數學歸納法本身產生懷疑。現筆者用例題加以說明，供同行參考，愿與同行探究.

一、使用不當

例1用數學歸納法證明

思考 顯然當n=1時有1＜2，命題成立

當n=1時有1＜2，命題成立

那么，當n=k+1時，有

命題成立，由數學歸納法得，原命題成立。

顯然，造成學生認為該題不能用數學歸納法的原因是，功力不夠，對數學歸納法使用不當。

二、設計加強命題

例2 用數學歸納法證明

思考 顯然，當n=1時，有1＜2，命題成立

則當n=k+1時

當n=1時，命題顯然成立

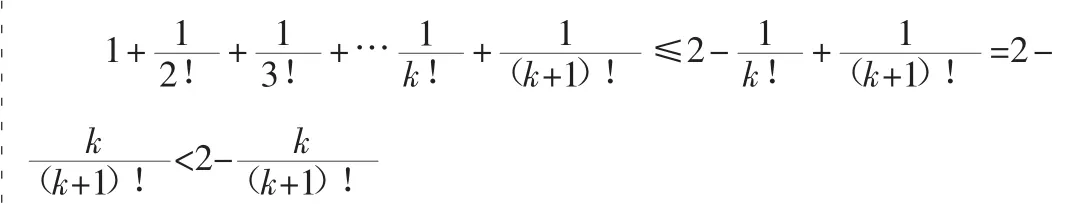
則當n=k+1時,有