融合傾斜儀數據的盾構姿態嚴密解算模型

潘國榮， 范 偉

(同濟大學 測繪與地理信息學院， 上海 200092)

盾構姿態的自動測量方法主要有激光標靶法、陀螺儀系統導向法、三棱鏡法、棱鏡和傾斜儀法.激光標靶法[1-3]主要根據CCD(charge coupled device)相機的相對位置確定盾構機的實時位置，但由于該系統相對比較復雜且CCD相機的大小有限，在實際應用中仍存在很多限制.陀螺儀系統導向法[4-6]長時間測量存在累積測量誤差，在施工中主要作為輔助參考測量.三棱鏡法[7-10]通過測量與盾構焊接在一起的3個棱鏡的坐標計算出盾首、尾在工程坐標系下的坐標，但由于隧道內空間狹窄且觀測條件惡劣，會出現棱鏡測量錯位或3個棱鏡無法全部觀測的情況，為了克服三棱鏡法的缺陷，在三棱鏡模型的基礎上引入了傾斜儀，即棱鏡和傾斜儀法[11].

棱鏡和傾斜儀法的系統構建簡單便捷，近年來得到了廣泛的研究，但仍存在3個方面的不足：第一，忽略了傾斜儀的標定誤差，將傾斜儀所測的俯仰角和滾動角直接作為盾構的俯仰角和滾動角[12]，或認為初始狀態下傾斜儀的俯仰軸和滾動軸與盾構的俯仰軸和滾動軸是平行的[13]，并通過理想化的幾何關系模型推求傾斜儀雙軸和盾構雙軸的關系，當標定誤差較大時，將嚴重影響盾構姿態測量的精度.第二，未對傾斜儀的采樣數據進行有效的預處理，無法保證傾斜儀采樣數據的精度和可靠性.第三，定權不合理，已有的棱鏡和傾斜儀數據的聯合平差模型將傾斜儀雙軸觀測數據視為等權獨立觀測值[14]，與實際的觀測模型不符.

為了解決上述問題，提出并論證一種嚴密的棱鏡和傾斜儀模型.推導傾斜儀與盾構的嚴密標定模型；將單次觀測周期中傾斜儀采集的多對雙軸角度數據視為平面點云，利用選權迭代法[15]對其進行穩健估計，以獲取單次觀測周期中傾斜儀數據的最佳估值及其協方差陣.在前述模型方法的基礎上，利用最小二乘配置方法[16]推導三棱鏡與傾斜儀數據融合的嚴密解算模型.最后，通過試驗，對上述模型方法進行分析驗證.

1 傾斜儀的嚴密標定模型

1.1 盾構標定坐標系的定義

如圖1所示，盾構標定坐標系為OXYZ，以盾尾為該坐標系O點，盾尾到盾首的方向作為X軸，Y軸位于水平面并垂直于X軸，Z軸垂直于XOY平面，形成左手坐標系.將盾構標定坐標系OXYZ繞其Y軸順時針旋轉β角，形成新的坐標系OvXvYvZv.可知2個坐標系之間存在如下轉換關系：

(1)

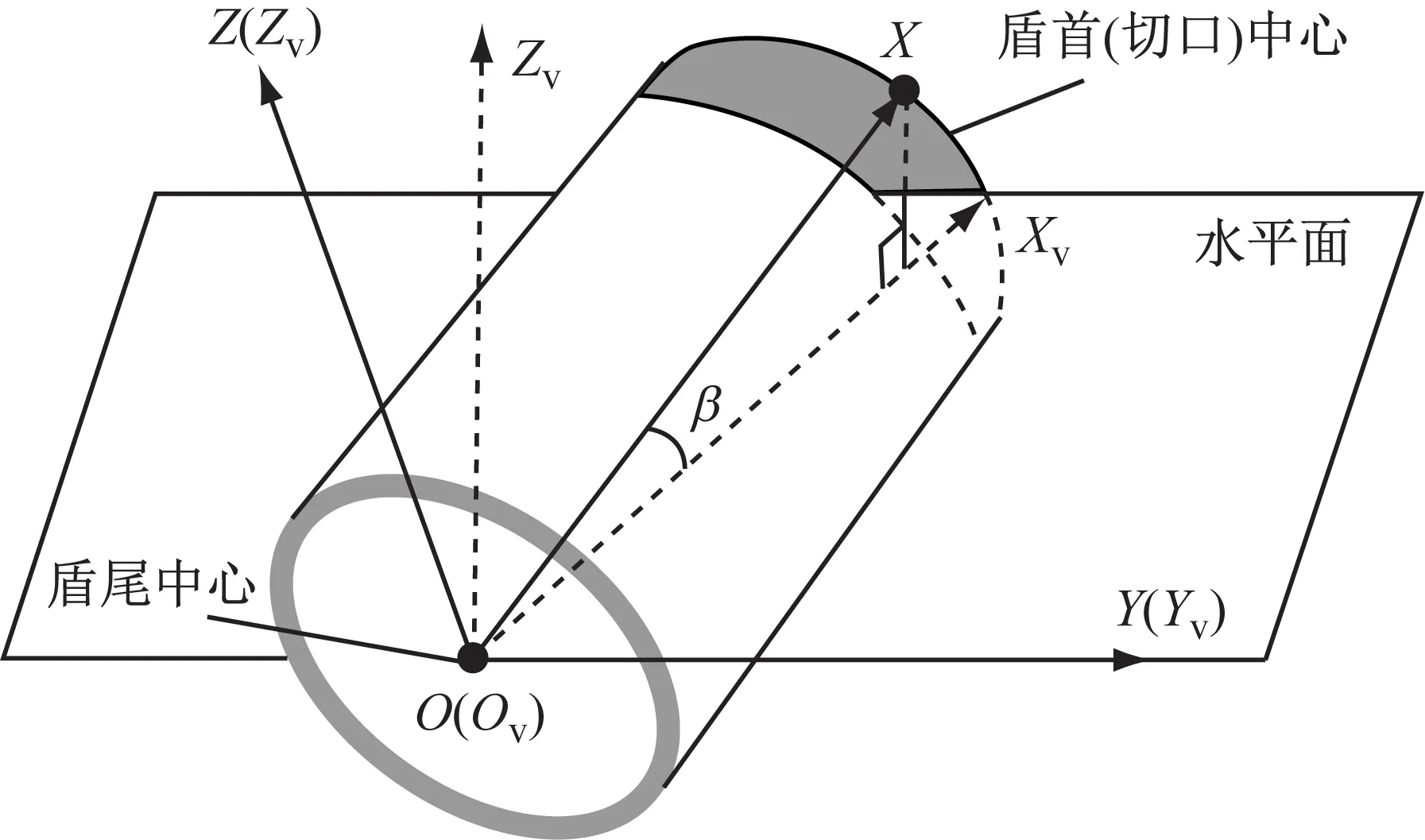
圖1 盾構標定坐標系(標定狀態)

1.2 傾斜儀坐標系的定義

如圖2所示，傾斜儀坐標系為OcXcYcZc，以傾斜儀俯仰軸方向為Xc軸，傾斜儀滾動軸方向為Yc軸，以Xc軸和Yc軸的交點作為傾斜儀坐標系的原點Oc，按左手坐標系規則確定Zc軸，其中ωp、ωs為初始狀態下傾斜儀所測俯仰角和滾動角.將傾斜儀坐標系OcXcYcZc繞Xc軸旋轉αt角，再繞Yc軸旋轉βt角，形成新的坐標系OcvXcvYcvZcv，可知2個坐標系之間存在如下轉換關系：

(2)

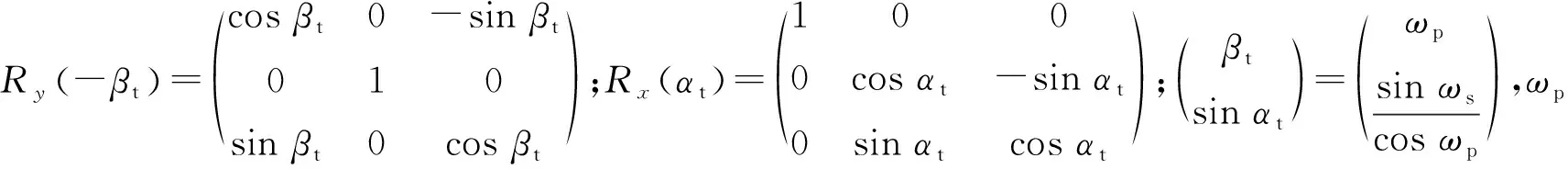
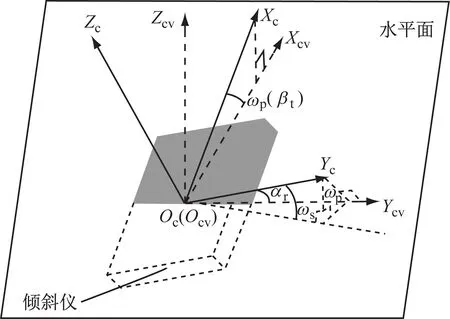
圖2 傾斜儀坐標系

1.3 傾斜儀坐標系與盾構標定坐標系的關系

傾斜儀標定模型使用向量作為坐標轉換的對象，因此，坐標系OvXvYvZv與坐標系OcvXcvYcvZcv的轉換關系在此僅考慮旋轉關系，如圖3所示，2個坐標系的轉換關系如下：

(3)

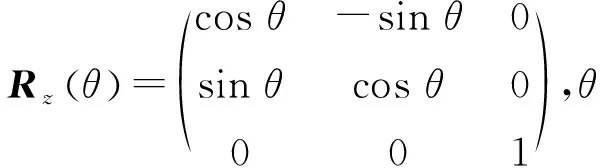
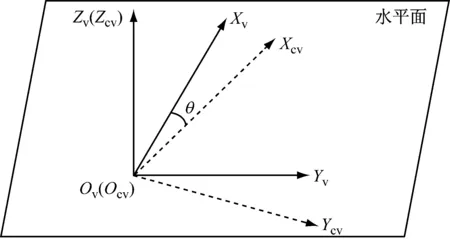
圖3 盾構標定坐標系與傾斜儀坐標系的關系

將式(1)和式(2)代入式(3)，可知傾斜儀坐標系OcXcYcZc與盾構標定坐標系OXYZ存在如下關系：

(4)

1.4 傾斜儀的嚴密標定模型

根據式(2)、式(3)和式(4)，可得盾構標定坐標系OXYZ與自定義坐標系OvXvYvZv關系為

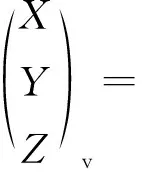
(5)

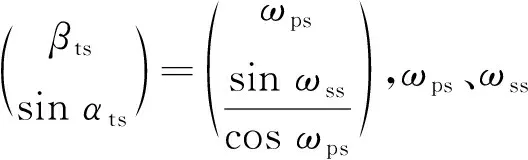
(6)

根據式(6)并結合圖4所示幾何關系，可得

(7)

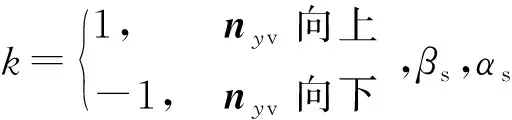
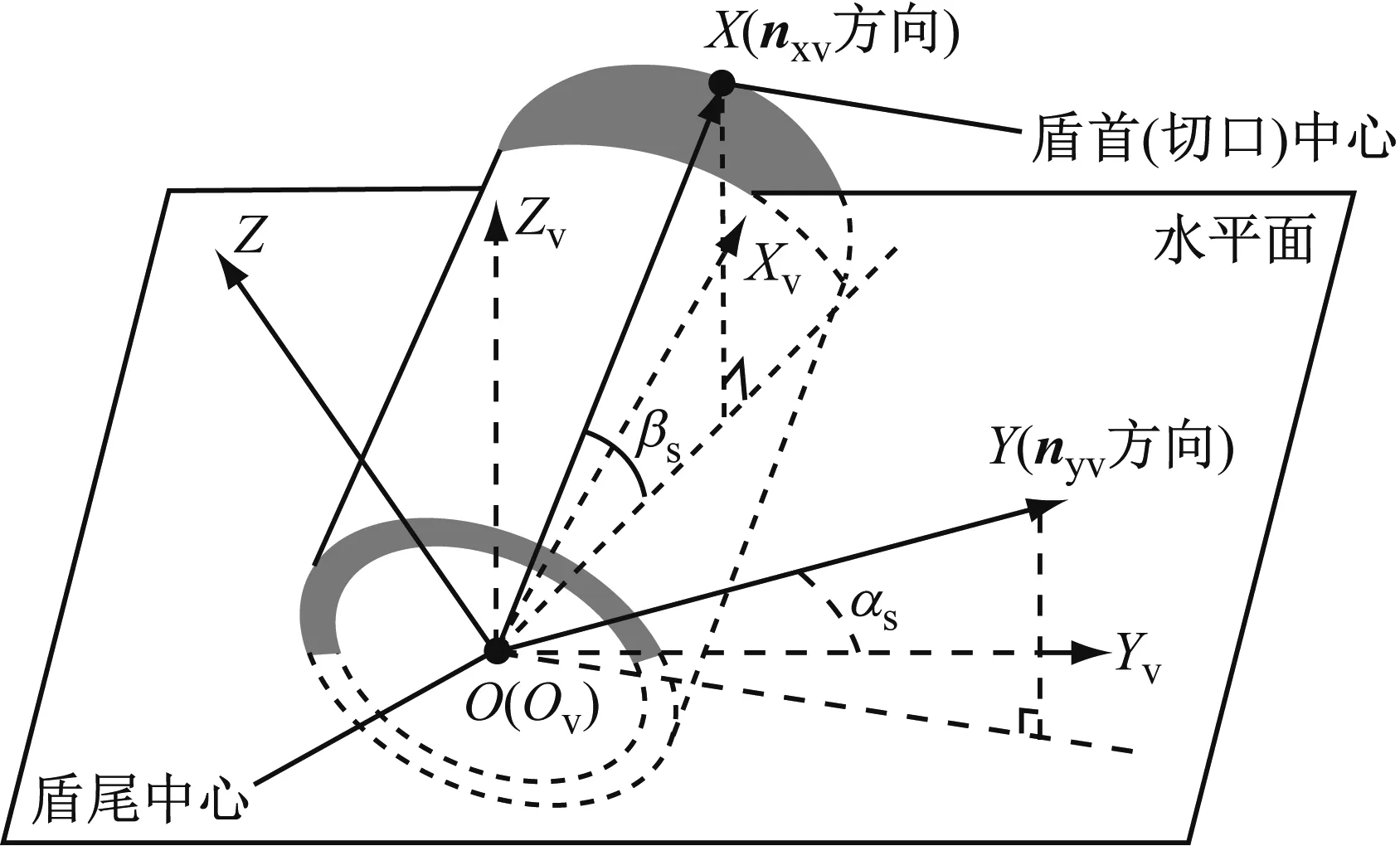
圖4 盾構標定坐標系(施工狀態)

2 傾斜儀數據的穩健估計方法

在棱鏡和傾斜儀法中，若以全站儀完整獲取所有棱鏡坐標的時間作為一個觀測周期，那么在一個觀測周期中傾斜儀可獲取幾十至上百對雙軸角度數據.因此，聯合平差前必須對傾斜儀獲取的雙軸角度數據進行有效預處理.由于一個觀測周期中傾斜儀采集的雙軸角度數據整體服從正態分布，但個別數據中含有粗差，所以在此基礎上推導傾斜儀雙軸角度數據的穩健估計方法.

2.1 建立傾斜儀數據的處理模型

將一個觀測周期中傾斜儀采集的雙軸角度數據視為平面點云，則傾斜儀數據的擬合即轉化為平面點云的擬合[17-18].根據加權最小二乘準則，得

(8)

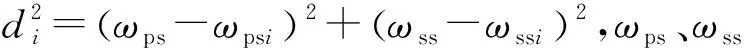
(9)

2.2 等效觀測值權函數的選擇

在一個觀測周期中，傾斜儀的個別采樣數據含有粗差，若認為等效觀測值di為等權觀測值，則平差結果無法反映觀測數據的真實分布情況，又無法抵抗粗差的影響.因此，使用等價權函數pi(vi)來確定等效觀測值di的權.將文獻[19]建議的等價權函數進行簡化并選取合適的迭代常數[20]，得

(10)

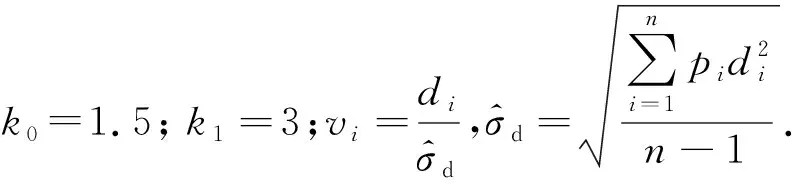
2.3 傾斜儀數據處理的選權迭代方法

在2.1節和2.2節的理論基礎上，通過選權迭代法處理傾斜儀的點云數據，迭代過程參見文獻

[15]，迭代結束后，將di視為等效觀測值，ωp、ωs視為待求參數，可根據間接平差原理列出誤差方程，并利用協方差傳播律求參數ωp、ωs的協方差陣，得

(11)

3 三棱鏡數據與傾斜儀數據融合的嚴密解算模型

(12)

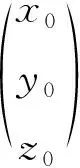
將式(5)代入式(12)可得，坐標系OpXpYpZp與坐標系OXYZ關系為

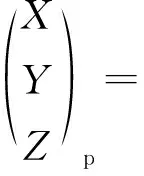
(13)

式中：Rc=Rx(-αt)Ry(βt)Rz(-θ)Ry(-β)，Rc初始標定時已知.

式(13)中，即含有非隨機參數(3個平移參數和1個旋轉參數)，又含有隨機參數(βts、αts)，所以，利用最小二乘配置法對式(13)進行平差處理.為了計算方便，用sinαts代替αts進行平差解算，由式(5)并根據協方差傳播律，可得βts、sinαts的協方差陣為

(14)

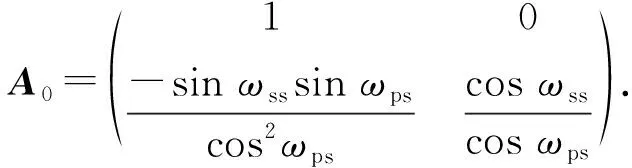
將βts、sinαts的先驗期望看作與棱鏡坐標觀測值相互獨立且方差陣為D1的虛擬觀測值，得

(15)

對式(15)進行線性化，可得誤差方程為

港口投資會增加港口的固定資產，如：碼頭岸線、岸吊、堆場、場吊、集卡和電子信息設備等。為增加運營設施/設備，需配備相應的工作人員。為服務這些新增的雇員還需增加服務業，這種溢出效果增加了臨港區域的就業與居住，提升港口城市的勞動力需求與工資水平。勞瑞模型可以刻畫這種溢出效應[10]，具體步驟為

V1=A11X1-L1

(16)

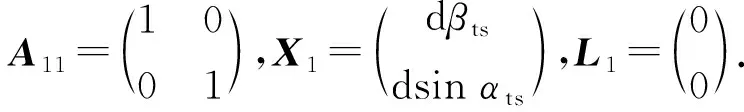
對式(13)進行線性化，可得每個棱鏡對應的3個坐標觀測值的誤差方程為

V2=A21X1+A22X2-L2

(17)

為敘述方便，所有棱鏡坐標觀測值的誤差方程仍用式(17)表示，在計算中只需對式(17)中的相應矩陣做擴充即可.根據自動全站儀標稱的測距和測角精度可計算三棱鏡對應的坐標觀測值的方差陣D2，并結合式(14)將式(16)和(17)聯立，根據廣義測量平差原理[21]，可得待求參數的最佳估值為

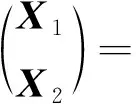
(18)

待求參數的協方差陣為

(19)

4 案例分析

4.1 傾斜儀標定誤差對盾構俯仰角和滾動角計算的影響

在初始狀態下，傾斜儀俯仰軸和滾動軸與盾構的俯仰軸和滾動軸，由于安裝誤差的限制，不可能保證嚴格平行.若忽略安裝誤差，認為傾斜儀雙軸與對應盾構雙軸是平行的，那么根據傾斜儀的俯仰角和滾動角計算出的盾構的俯仰角和滾動角必然與本文所述的正確模型計算出的結果存在偏差，如下式：

(20)

式中：βs、αs表示使用本文所述的正確模型計算出的盾構的俯仰角和滾動角；βw、αw表示忽略安裝誤差所計算出的盾構的俯仰角和滾動角.

若初始狀態不存在安裝誤差，即傾斜儀雙軸與對應的盾構雙軸平行，則相應的角度應滿足下式：

(21)

式中：δ的單位為角度；為了方便計算且不失一般性，令β為1°.

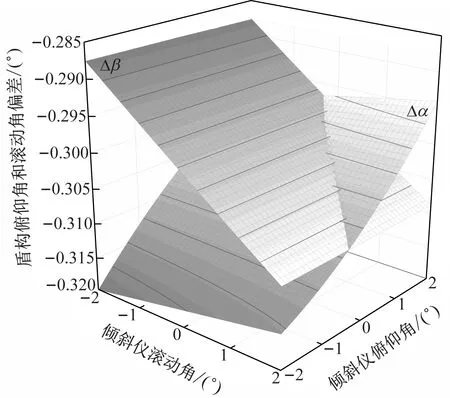
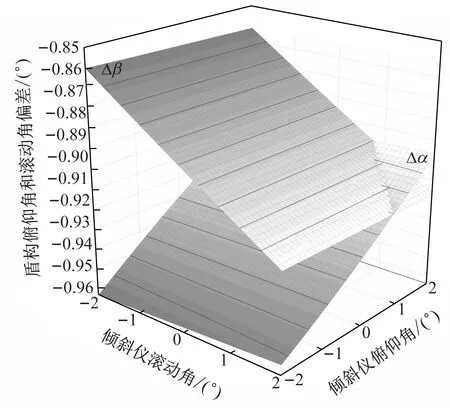
圖5傾斜儀標定誤差對盾構俯仰角和滾動角計算的影響

Fig.5Influenceofthecalibrationerroroftheinclinometeronthecalculationofshield’spitchingangleandrollingangle

對圖5分析可知，若使用忽略傾斜儀安裝誤差的模型計算，傾斜儀的安裝誤差越大，盾構俯仰角與滾動角計算的偏差越大，且盾構俯仰角與滾動角計算的偏差與傾斜儀的安裝誤差處于一個量級；當傾斜儀隨盾構一起發生扭轉時，傾斜儀的安裝誤差越大，盾構俯仰角與滾動角計算的偏差的波動越大.

4.2 傾斜儀數據穩健估計方法的驗證

以期望為0°、標準差為0.005°分別生成2組各100個服從正態分布的隨機數，并將其分別加入傾斜儀所測俯仰角和滾動角的真值上，形成100對含有隨機誤差的傾斜儀觀測數據，并在第26對、49對、73對觀測數據的俯仰角和滾動角中均加入粗差，在第17對觀測數據的俯仰角、第88對觀測數據的滾動角中加入粗差，粗差的大小為3倍標準差，最終形成一組傾斜儀模擬觀測數據，如圖6所示.

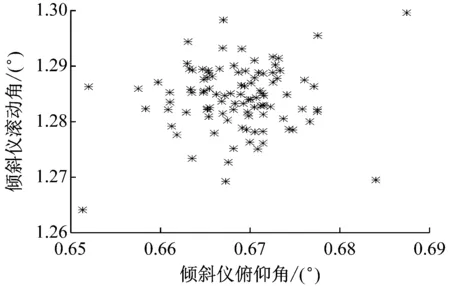
圖6 傾斜儀的模擬觀測數據

利用本文所述的穩健估計方法，對上述數據進行處理，所得結果見表1.

表1 傾斜儀模擬觀測值的平差結果

根據表1，本文模擬的數據的平差結果與其真值的差值遠遠小于模擬觀測值的標準差0.005°，由此可認為平差結果不受粗差的影響而只受偶然誤差的影響，從而證明了本文提出的針對傾斜儀觀測數據的穩健估計方法是有效可行的.

4.3 棱鏡數據與傾斜儀數據聯合平差模型的驗證

試驗數據由實測數據和模擬數據共同組成.表2所示為某工程的實測數據.

設計了2組傾斜儀標定數據和觀測數據.在標定狀態下，傾斜儀的俯仰角為ωp，滾動角為ωs，傾斜儀俯仰軸與盾構俯仰軸在水平面的夾角為θ；在施工狀態下，相應傾斜儀觀測的俯仰角為ωps，滾動角為ωss，如表3所示.

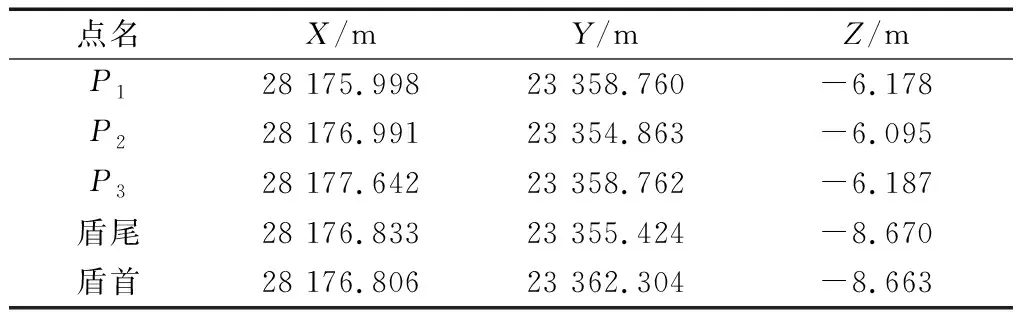
表2 棱鏡和盾首、尾的初始測量數據

使用2種聯合平差模型對上述數據進行處理.第1種模型認為，在初始狀態下，傾斜儀的雙軸與對應盾構的雙軸是平行的，即傾斜儀存在標定誤差，但模型中予以忽略.第2種模型為本文提出嚴密聯合解算模型，即認為，在初始狀態下，傾斜儀的雙軸與對應盾構的雙軸不平行.

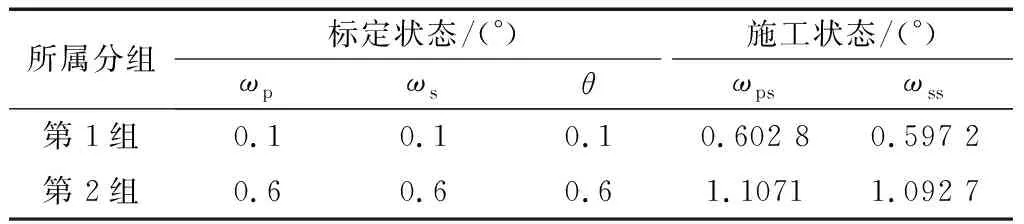
表3 傾斜儀標定狀態及其對應施工狀態下的觀測數據

使用第1種聯合平差模型，根據表3中2組傾斜儀的模擬數據，并分別結合2個棱鏡和3個棱鏡的觀測數據，解算的盾首、尾坐標與其真值的差值，如表4所示.表中，P1、P2、P3表示棱鏡.

表4 第1種平差模型的解算效果

使用第2種平差模型，根據表3中2組傾斜儀的模擬數據，并分別結合2個棱鏡和3個棱鏡的觀測數據，解算的盾首、尾坐標與其真值的差值，如表5所示.

表5 第2種平差模型的解算效果

對表4和表5進行分析可知，① 若以50 mm作為隧道貫通的測量限差，使用第1種聯合平差模型，當傾斜儀的標定誤差在0.1°時，盾首、尾坐標的聯合平差結果的偏差屬于毫米級，仍能滿足隧道貫通精度的要求.但隨著標定誤差的增大，當傾斜儀的標定誤差達到0.6°時，盾首、尾坐標的平差結果的偏差已超出隧道貫通限差的要求.② 使用第1種聯合平差模型，棱鏡個數的增加并不能提高聯合平差結果的精度，即三棱鏡數據和傾斜儀數據的聯合平差結果與兩棱鏡數據和傾斜儀數據的聯合平差結果在精度意義上是一致的.③ 使用第2種平差模型對棱鏡和傾斜儀數據進行處理，計算結果的偏差均在亞毫米級，甚至優于亞毫米級，證明了本文所建立模型的正確性和穩定性.

5 結論

通過研究初始狀態下傾斜儀和盾構的空間位置關系，建立了傾斜儀與盾構的嚴密標定模型.將傾斜儀的雙軸角度觀測數據視為平面點云，對傾斜儀數據進行穩健估計.在傾斜儀與盾構的嚴密標定模型基礎上，建立了盾構標定坐標系與工程坐標系的轉換關系，并利用最小二乘配置方法將傾斜儀相關數據視為具有先驗統計信息的虛擬觀測值，在廣義最小二乘原理下，建立了傾斜儀數據與棱鏡數據的聯合解算模型.最后，通過試驗分析了傾斜儀標定誤差對盾構俯仰角和滾動角計算的影響；分析了傾斜儀數據穩健估計的效果；分析了本文建立的聯合平差模型的解算精度，并與不考慮傾斜儀標定誤差的聯合平差模型進行了對比，驗證了本文聯合平差模型的正確性和可行性.提出的傾斜儀數據與棱鏡數據的聯合平差模型建立在傾斜儀與盾構嚴密標定模型的基礎上，該標定模型也可靈活應用于其他使用傾斜儀進行姿態測量的工程中.