船舶重量分布載荷強度計算方法研究

楊亢亢，宋 達

(中國艦船研究設計中心，湖北 武漢 430064)

0 引 言

重量曲線是描述船舶重量沿船長分布狀況的曲線[1]，其縱坐標表示作用于單位長度上的重量分布載荷強度，是船舶防縱傾設計的重要設計指標[2]。通常將各項重量按靜力等效原則分布在相應的理論站距范圍內，再逐項迭加得到各站距內的重量分布載荷強度，以便繪制船舶重量曲線分布圖。

在計算單個設備或物品的重量分布載荷強度時，一般將重量沿設備或物品所處標準理論站距進行等效分布載荷計算[3–4]。當設備或物品在船首/船尾有一定的延伸部分時，若突出部分未超過理論站距一半，且突出部分重量占空船重量的比例小于1%時，一般認為可將突出部分忽略不計處理；若突出部分超過理論站距一半之多時，則將重量按長度進行重量分段處理，再進行船首、船尾的重量等效轉移到相鄰的2個理論站距內。

隨著船舶設計質量的不斷提高，對重量分布載荷強度的計算精度提出了更高的要求。針對設備或物品突出部分重量的傳統處理方法，在一定程度導致部分重量缺失或等效分段重量失真等情況[5–6]，無法滿足高精度的設計需求。本文將船首、船尾分別視為一個完整的理論站距，將20個理論站距擴充到22個，計算設備在各理論站距內的重量分布載荷強度，再將船首、船尾2個理論站距載荷強度折算到相鄰的2個理論站距，得到20個理論站距的船舶重量分布載荷強度，避免船首、船尾的部分重量缺失或失真，使重量分布載荷強的更加準確。

1 重量分布載荷強度分布原則

考慮到設計水線是船舶運行過程中穩性安全的重要保證，沿設計水線方向劃分理論站距更真實地反映出船舶的重量分布，確保重量分布合理，保障運行安全。圖1為船舶重量分布曲線圖，將全船沿設計水線方向劃分為20個理論站，對各項重量進行近似和理想化分布處理時，必須遵循以下靜力等效原則[7]：

1）保持重量的大小不變，即等效后各理論站距的重量之和應近似等于該設備的實際重量；

2）保持重量重心的縱坐標不變，即等效后形心縱坐標與該設備的重心縱坐標相等；

3）近似分布曲線的范圍與該項重量實際分布范圍相同或大體相同。

最終，應使重量分布曲線所圍面積等于全船的重量，該面積的形心縱坐標與重心的縱坐標相同。

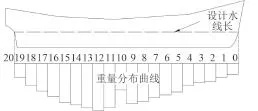
圖 1 船舶重量分布曲線Fig. 1 Distributed curve of ship weight

2 重量分布載荷強度計算模型

2.1 兩個理論站距內的重量分布載荷強度

如圖2所示，某項以任意規律分布在2個標準理論站距內的重量為P，重心距2站的距離為α，按照分布原則3，用1-2及2-3兩個理論站距內的分布載荷代替真實的重量分布。設2個理論站距內的重量分別是P1和P2，根據分布原則1和分布原則2可得：

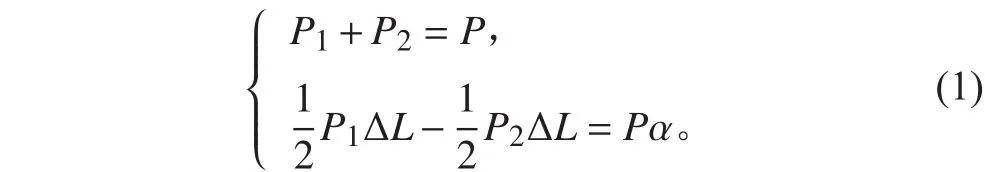
將P1和P2除以理論站距長度ΔL，即可得到該項重量在2個理論站距內的分布載荷強度。

圖 2 在2個理論站距內的重量分布載荷圖Fig. 2 Weight distributed loading between two theoretical stations

2.2 三個理論站距內的重量分布載荷強度

如圖3所示，當重量分布在3個理論站距時，根據靜力等效原則只能列出2個方程式，無法求解3個未知數，因此，一般用1.5ΔL代替ΔL，利用公式（1）求得P1和P2，再利用公式（1），將P1和P2分別向其相鄰的2個理論站距內分布，最后將中間理論站距迭加來自P1和P2的相應分配值，即為中間理論站距內的重量分布。

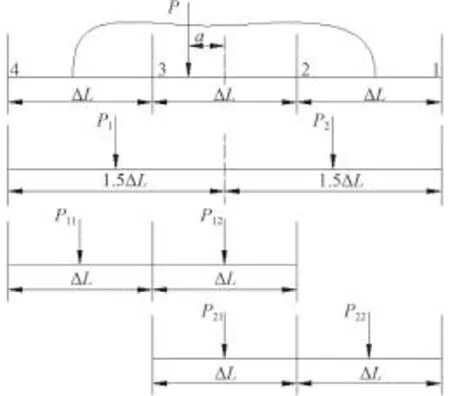
圖 3 在3個理論站距內的重量分布載荷圖Fig. 3 Weight distributed loading between three theoretical stations

將各理論站距內分配得到的重量分別除以理論站距長度ΔL，即可得到該項重量在3個理論站距內的分布載荷強度。

2.3 船首/船尾理論站距的重量分布載荷強度

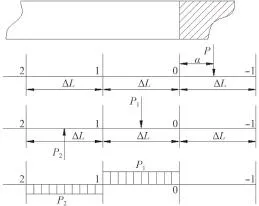
圖 4 船首、船尾理論站距的重量分布載荷強度圖Fig. 4 Weight distributed loading between bow and stern

如圖4所示，當重量分布在船首、船尾時，將船首、船尾當成一個標準理論站距來處理，將該理論站距內的重量轉移到相鄰的2個理論站距內，根據靜力等效原則不改變其重量大小及其對船中的力矩大小，可得到式（3）。

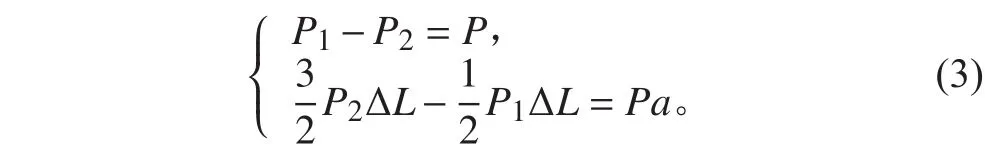
將P1和P2除以理論站距長度ΔL，即可得到船首、船尾的重量折算至相鄰2個理論站距內的分布載荷強度。

對于在更長范圍內分布的重量，計算時只要將理論站距ΔL用分布范圍內的等分段長度代替即可。

3 重量分布載荷強度計算方法

本文將船首和船尾分別作為一個完整的理論站距，將20個標準理論站距擴充到22個標準理論站距，根據靜力等效原則將船上各設備或物品的重量等效分布在該設備或物品所在的理論站距范圍內的各標準理論站距上，然后將分布在船首標準理論站距和船尾標準理論站距內的重量折算至與其相鄰的2個標準理論站距內，最后得到20個標準理論站距的重量分布，具體計算流程如圖5所示。

1） 理論站距信息計算

以船腫肋位號FR的一半為坐標原點，根據設計水線長L、肋骨間距S計算22個標準理論站距信息（包括幾何中心縱坐標、起始縱坐標和終止縱坐標）：

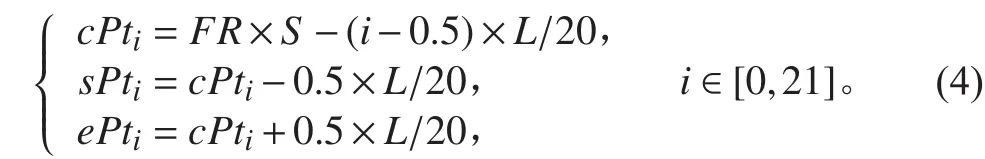
其中：i表示第i個理論站距的編號，cPti為第i個理論站距的幾何中心縱坐標，sPti為第i個理論站距的起始縱坐標，ePti為第i個理論站距的終止縱坐標；L為設計水線長、S為肋骨間距、FR為船中肋位號。所有理論站距信息都可以表示為向量的形式，形成理論站距中心坐標矩陣cPt和坐標信息矩陣 A rea：

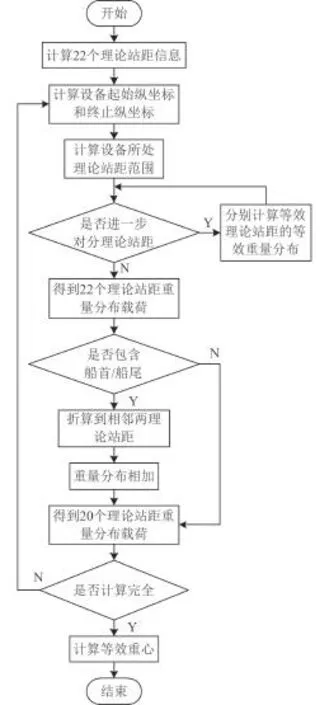
圖 5 船舶重量分布載荷強度計算流程圖Fig. 5 Calculation flow of ship weight distributed loading

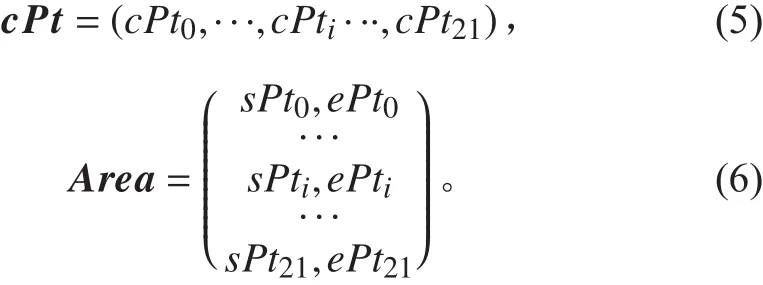
2） 設備信息計算

根據設備的起始肋位號sFR和終止肋位號eFR計算設備的起始縱坐標sX和終止縱坐標eX：

3） 計算設備所處理論站距范圍

特殊地，當設備或物品的重心縱坐標cX處于船首、船尾標準理論站距時（即船首或船尾），則認為該設備重量集中于該標準理論站距，其所處理論站距為船首/船尾標準理論站距，所處標準理論站距個數為1；當設備起始肋位號和終止肋位號相同時，則認為該設備重量集中于重心縱坐標cX處，其所處理論站距為重心縱坐標cX所在標準理論站距，所處標準理論站距個數為1。

4） 計算設備所處的各理論站距內的重量分布

當設備所處的理論站距范圍內標準理論站距的個數大于或等于2時，將該設備的重量按照靜力等效原則等效至該設備所處的各標準理論站距上，計算設備所處的各標準理論站距內的重量分布，具體計算步驟如下：

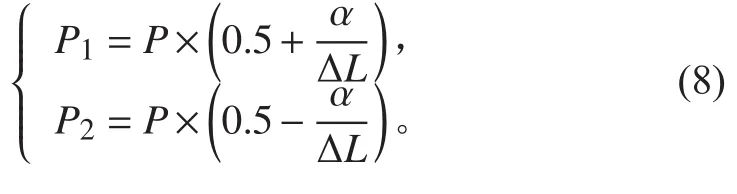
其中：P為設備重量，α為該設備重量作用點與所處的理論站距范圍的幾何中心之間的距離；?L為對分后的等效理論站距的長度。

5） 若該設備跨船首、船尾標準理論站距，則將船首、船尾標準理論站距的重量分布折算至相鄰的2個標準理論站距內（見圖4），可用公式（3）計算得：

其中： ? L′為船首、船尾標準理論站距長度；折算船首標準理論站距內的重量時， α′為船首標準理論站距內的等效重力P的作用點與船首標準理論站距終止縱坐標之間的距離；折算船尾標準理論站距內的重量時，為船尾標準理論站距內的等效重力P的作用點與船尾標準理論站距起始縱坐標之間的距離

6）將該設備各理論站距內重量分布相加，除以標準理論站距長度，即可得到各理論站距的重量載荷分布強度：

其中，Pi表示第i個理論站距的重量載荷分布強度。

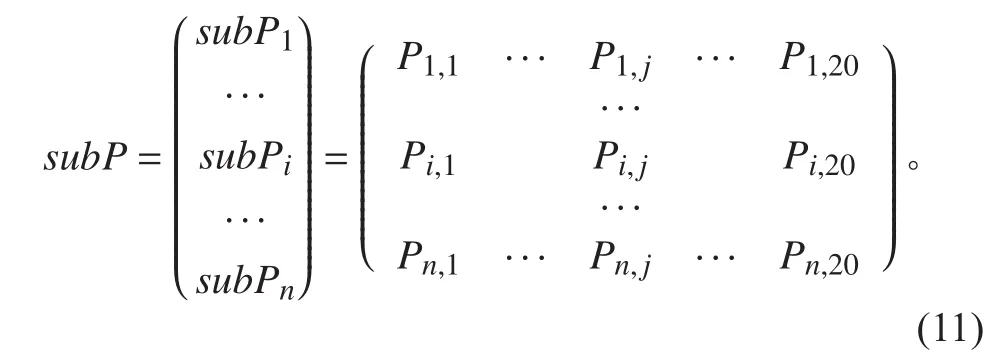
7）依次對全船所有設備計算各理論站距的重量載荷分布強度：其中：subPi為第i個設備的重量載荷分布，Pij為第i個設備在第j個理論站距的重量載荷分布強度，n為設備個數。將各理論站內所有設備的重量分布載荷強度相加，即可得到第j個理論站距內的重量分布載荷強度：

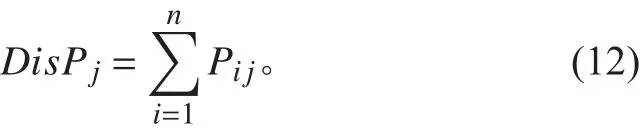
將每一個理論站距的重量載荷分布強度表示為向量形式，形成重量縱向分布載荷強度矩陣：

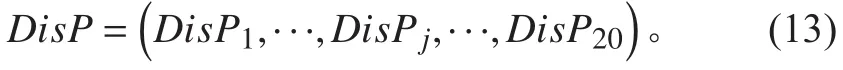
8）根據各理論站距的中心坐標cPt和等效重量分布載荷DisP計算重量分布之后的等效重心坐標：

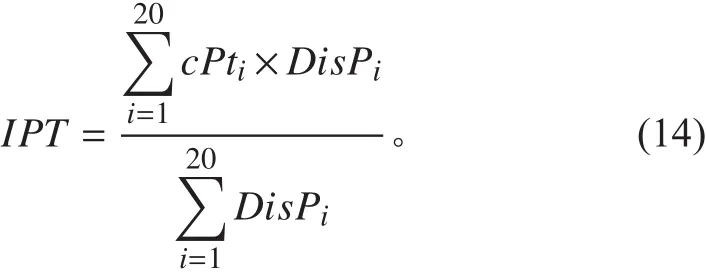
4 應用實例

船舶重量分布載荷強度計算軟件以Excel為計算工具，利用Office軟件內嵌的面向對象編程語言VBA（Visual Basic for Application）語言對其進行了二次開發[8–9]，通過 XML DOM Document對象實現 Excel與PDM之間的數據交互[10]，讀取PDM系統中各設備的坐標信息，如圖6和圖7所示。

以某型船舶為例，其總體參數如表1所示，經船舶某設計專業計算后，該設備重量分布載荷強度如圖8所示。

可知，此重量載荷強度分布方法較為真實地反映了實際的重量分布規律，在此基礎上可進一步實現貨物、燃油、淡水、旅客等重量分布設計，以及靜水剪力、彎矩、擾度等計算。

5 結 語

圖 6 船舶重量分布載荷強度計算軟件界面Fig. 6 Software interface of ship weight distributed loading

圖 7 PDM 中設備重量中心信息Fig. 7 Information of device weight center in PDM

表 1 船舶總體參數表Tab. 1 Overall parameters of ship

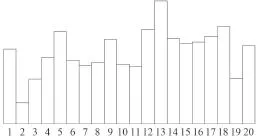
圖 8 重量載荷強度分布圖Fig. 8 Distributed curve of ship weight

本文在分析了船舶重量分布載荷強度分布原則的基礎上，研究了重量分布載荷強度的基本計算模型，設計了將船首、船尾分別視為一個完整的理論站距的重量分布載荷強度計算方法，以Excel為計算工具，通過VAB開發與PDM實現數據交互，讀取PDM系統中各設備的坐標信息，并結合實例進行了應用。該計算方法能夠避免設備在船首、船尾的部分重量缺失或失真，能更真實地反映出船舶的重量分布，也為船舶行業重量分布載荷強度計算提供了一種快速、規范的計算方法。