舷側不連續雙層板架結構穩定性試驗及改進設計

鄧賢輝，梅國輝，駱 偉，閆小順，吳衛國

(1. 海軍駐上海江南造船集團有限責任公司軍事代表室，上海 201913；2. 中國艦船研究設計中心，湖北 武漢 430064；3. 武漢理工大學 高性能艦船技術教育重點實驗室，湖北 武漢 430063)

0 引 言

船舶的極限承載能力是指船舶在航行過程中，在極端荷載條件下抵抗縱向彎曲的能力[1]。其中，甲板與和甲板相連的舷側結構的屈曲失效對整個船舶極限承載能力有著不可忽視的影響[2-3]。當船舶具備舷側大開口結構時，其極限承載能力會因舷側結構的不連續性而明顯降低。因此，針對具有舷側大開口結構的板架模型，研究其板與筋的組合形式以及板厚的分布情況對整個板架結構的極限承載能力的影響，對評估整船結構的極限承載能力有著重要的意義。

針對局部結構的尺寸優化和形狀優化技術已相當成熟。板架優化中多數選取船底板架、艙壁板架結構和上層建筑板架結構等復雜結構，針對結構形狀、構件布置和尺寸優化設計方法等方面進行分析，提高船舶在實際工程設計中的可行性與實用性。優化內容包括板架最佳形式、構件最佳形狀和最佳尺寸等，最終得出基于實際工程設計的優化模型和設計變量形式，以達到增加結構強度、優化結構布置、減輕結構重量等目的[4]。

1 初始舷側大開口板架模型試驗及數值仿真驗證

極限強度定義的船體結構破壞形式包括屈服、屈曲及組合的各種形式和構件之間的非線性影響[5]。由于甲板結構的極限破壞是一個漸進的過程，同時涉及到幾何非線性和材料非線性問題，又存在板和筋的多種組合失效模式，其屈曲失效過程十分復雜。直至目前，試驗研究方法以其直觀性的特點在船舶結構極限強度研究領域具有舉足輕重的地位，對深入認識結構的整個失效過程有著重要的意義。本文首先設計了舷側布置有大開口的雙層板架結構，并開展了舷側大開口結構板架模型的破壞試驗，得到該板架模型的極限承載能力，并在此基礎上采用非線性有限元軟件對其進行了軸向壓載仿真計算。

1.1 板架結構模型

本文選取某具有舷側大開口結構以及甲板大開口結構的雙層甲板板架結構為研究對象，圖1為該結構甲板的CAD圖，圖2為該結構舷側結構的CAD圖。模型長度為 2 858 mm，寬度為 2 580 mm，高度為465 mm。各構件具體尺寸如表1所示，模型材料統一采用屈服應力為345MPa的Q345鋼材。

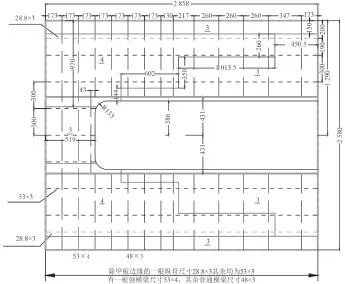
圖 1 甲板結構 CAD 圖Fig. 1 The CAD diagram of the deck structure

圖 2 舷側結構 CAD 圖Fig. 2 The CAD diagram of the side structure

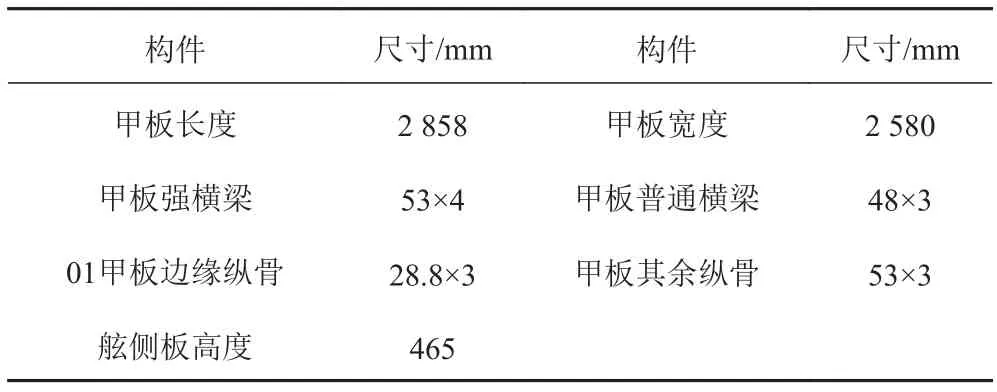
表 1 雙層甲板板架結構主要構件尺寸Tab. 1 The main dimensions of the double deck frame member structure

1.2 試驗加載及數據采集系統

將鋼制模型置于由2個門架組成的自平衡加載系統中，模型采用一端固支、一端簡支的邊界條件[5]。固支端使用工裝固定在橫梁上，簡支端使用液壓千斤頂系統施加軸向載荷。

模型所受軸向載荷使用壓力傳感器測量，壓力傳感器布置于液壓千斤頂和模型加載端之間。模型兩端分別對稱布置3個百分表，以測量結構的軸向變形。模型上布置有66個應變測點，大開口周圍為主要關注區域，均布置三相應變片，其余區域主要布置單向應變片。試驗加載及數據采集系統如圖3所示。

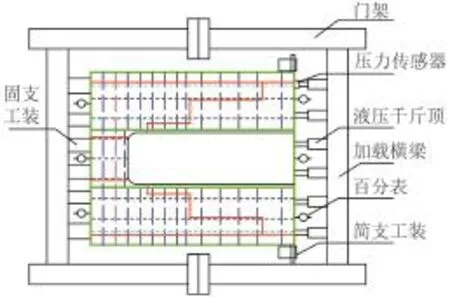
圖 3 試驗加載示意圖Fig. 3 Schematic diagram of the test load

為模擬簡支邊界條件，在圖2中結構左端甲板與舷側板交界處布置橫向銷軸，銷軸可在固定于地基上的方鋼內沿模型長度方向自由滑動，但是無法沿模型高度方向運動。從而限制了模型左端高度方向的位移，放開了長度方向的位移和寬度方向的轉角，滿足簡支邊界條件的需求，工裝如圖4（a）所示。為模擬固支邊界條件，使用十字支柱將圖1 中結構的右端固定在橫梁上，如圖4（b）所示。

1.3 模型試驗及試驗結果

為了減小焊接殘余應力的影響，在破壞性試驗開展之前進行3次線彈性范圍內的載荷加載[6]，同時調試應變測點及數據采集系統。加載過程采用逐步加載方式，設置每級載荷為60 kN。第1次預加載最終載荷為480 kN，然后逐級卸載至0；第2次和第3次預加載最終載荷均為540 kN，然后逐級卸載至0。預加載之后進行破壞性試驗，開始先以60 kN為一個載荷增量步，當載荷達到660 kN的時候，將載荷增量步調整為18 kN，直至結構屈曲失效，無法繼續承載。

在逐級加載的過程中，每達到一個載荷點，待壓力傳感器讀數穩定后，同時采集壓力傳感器讀數、百分表讀數和各應變測點讀數。在壓力傳感器的讀數突然下降的時候，采集最后一組數據。該破壞試驗的載荷位移曲線如圖5所示。

圖 4 模型邊界條件Fig. 4 The boundary condition of the model

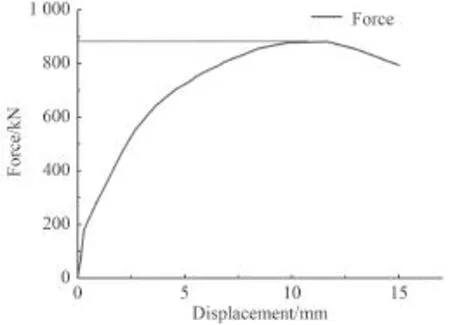
圖 5 破壞試驗結構位移載荷曲線Fig. 5 The load-displacement curve of structure in destructive testing

由圖5試驗數據分析可知，該初始舷側大開口板架模型的極限承載能力為888 kN。

非空間大數據的存儲主要采用Hadoop分布式文件系統，存儲策略主要包括三部分內容：首先根據數據特點進行屬性分類，將同屬同一類的小文件聚合成為一個大的文件，便于提高小文件的讀寫速度；然后在合并小文件的過程中，需要建立相對應的檢索系統，以此快速訪問小文件[5]；最后建立合理的緩存的體系，對文件存放的數據塊進行緩存，從而提高訪問小文件的效率，大大縮短了訪問的時間。

1.4 板架有限元仿真與模型試驗極限強度對比驗證

根據舷側大開口板架CAD模型的設計，采用Solidworks軟件創建仿真實驗模型的三維模型，并利用Hypermesh軟件劃分模型網格，該有限元模型的網格大小為30 mm，整個模型劃分網格38 181個，節點41 320 個。

板架結構有限元模型兩端分別采用MPC約束，在設置邊界條件及載荷施加時，僅對MPC點進行操作即可，如圖6所示。邊界條件詳細設置如表2所示。板架結構的左端工裝完全固支，右側則放開Y軸方向的自由度。

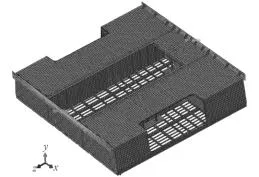
圖 6 有限元模型約束及加載方式Fig. 6 Constraint and loading of finite element model

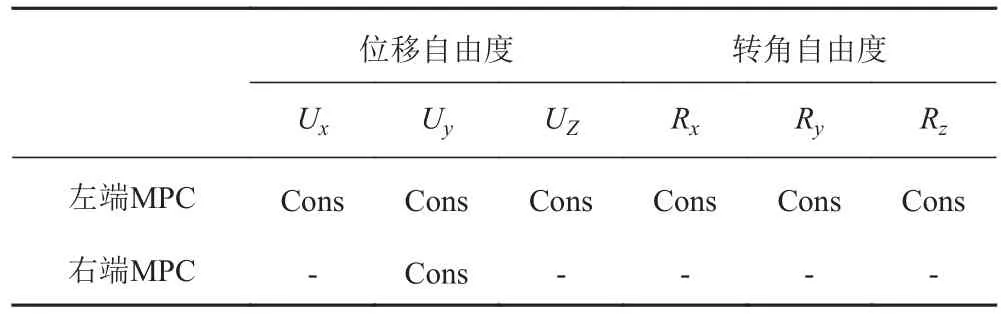
表 2 板架模型兩端邊界約束條件Tab. 2 Boundary constraints on both ends of model

將初始板架有限元模型計算結果與破壞試驗的結果進行對比分析，可得如圖7所示的力載荷-位移曲線。

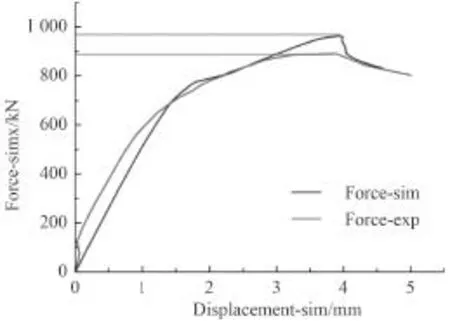
圖 7 有限元模型、試驗模型載荷-位移曲線對比Fig. 7 Comparison of load - displacement curve of finite element model and test model

由有限元模型、試驗模型集中力載荷-位移曲線結合試驗情況記錄圖可知，隨著軸向加載載荷的增大，軸向壓縮的位移呈增長趨勢。隨著載荷的逐漸增大，不連續甲板大開口區域出現屈曲現象；當集中力載荷達到959.02 kN時，縱艙壁處出現屈曲破環，整體板架失穩，同時載荷達到峰值；甲板和縱艙壁作為船體板架主要承力構件發生破壞，失去承載能力，外界載荷無法繼續增加。對比舷側大開口板架試驗模型測試結果曲線Force-exp與有限元模型載荷-位移曲線Forcesim，發現兩者的曲線趨勢大致相同。同時，將試驗與仿真計算的屈曲破壞的形式進行對比，如圖8和圖9所示。

圖 8 試驗模型屈曲破壞圖Fig. 8 The buckling failure diagram of the test model

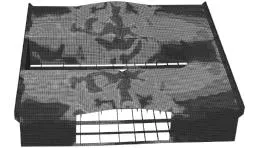
圖 9 有限元仿真計算破壞圖Fig. 9 Damage diagram of finite element simulation calculation

由圖7可知，初始舷側大開口有限元板架模型和試驗板架模型屈曲強度分別為959.02 kN和888 kN。有限元板架模型和試驗板架模型的相對誤差為7.4%，如表3所示符合工程要求。同時，從圖8和圖9的對比可知，試驗模型屈曲破壞的形式同本論文所采用的有限元仿真計算方法得到的破壞形式吻合度較高，本論文所采取的數值仿真方法也同時得到相應的驗證。

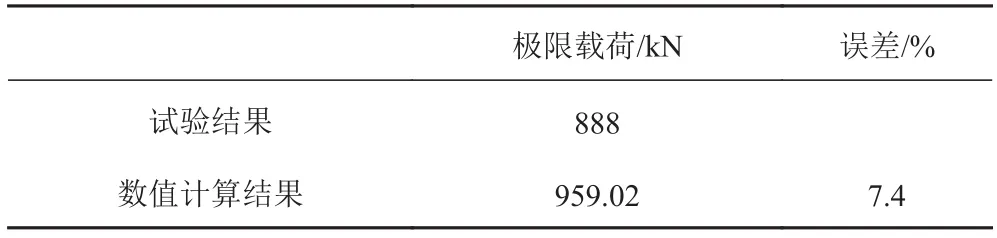
表 3 極限載荷對比Tab. 3 Comparison of ultimate loads

2 舷側大開口板架結構改進方案及仿真結果分析

2.1 舷側大開口板架模型破壞過程及失效誘因分析

通過對試驗及仿真分析過程的觀測，發現隨著載荷的增大，該雙層板架結構在舷側大開口角隅處首先發生明顯的屈曲破壞，甲板與縱艙壁交界處甲板達到屈服應力并發生了屈曲，如圖10（a）所示。同時，甲板大開口角隅處發生應力集中現象，材料達到屈服極限，但未產生屈曲現象。縱艙壁局部應力集中，達到屈服極限但并未產生屈服現象。橫艙壁以及甲板的其他區域材料未達到其屈服極限，如圖10（b）所示。

圖 10 結構破壞模式Fig. 10 Failure mode of the structural

同時，由圖10（b）可知，舷側開口區域縱骨發生側向失穩，且越接近舷側大開口處的甲板屈曲區域縱骨失穩情況越嚴重。這種局部的屈曲失穩導致了整個板架模型最終的破壞。由此可見，甲板板的厚度不足及縱骨的尺寸較小為該結構屈曲失效的主要誘因。

2.2 舷側大開口甲板板架優化思路

通過上述分析可知，舷側大開口的角隅附近的結構強度較弱，易導致結構的整體屈曲失效。可通過增加該區域的甲板板厚、在局部增加橫梁結構以及增大圍緣扁鋼的尺寸等方法來對該區域的結構強度進行加強，從而提高該甲板板架的承載能力。同時，在進行板架屈曲分析時，要考慮筋對其臨界應力的影響，筋尺寸和形式的不同，影響程度也不一樣[6]。

橫艙壁、縱艙壁以及舷側結構的應力值較低，故無需對其進行加強。結構屈曲區域的縱桁和橫梁結構，當甲板發生屈服時，引起了其上的應力突增，產生了較小的塑性變形，由于結構發生屈曲時，縱桁和橫梁的承載能力損失較小，故對其無需進行結構加強。

2.3 改進方案設計

結合上述優化思路，提出4種改進方案（見表4）。具體的改進區域如圖11所示。

2.4 各改進方案數值仿真結果對比與分析

保持載荷加載方式以及邊界條件與原始方案相同，分別對以上4種優化方案進行有限元數值計算，當甲板板架達到極限承載能力時，其應力云圖如圖12所示。

表 4 四種改進方案Tab. 4 Four kinds of improvements

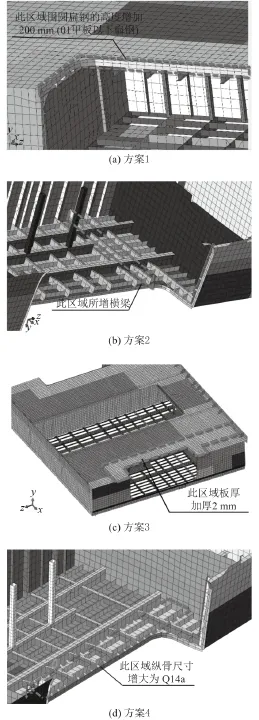
圖 11 改進區域及措施示意圖Fig. 11 Improved area and improved measures

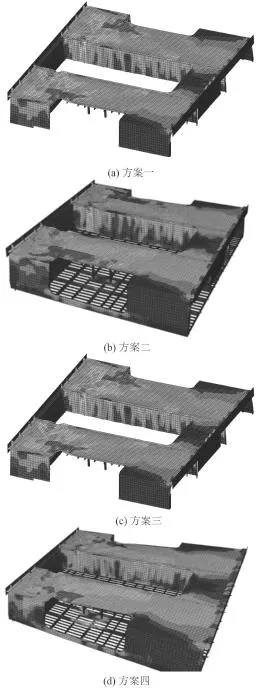
圖 12 四種改進方案仿真結果應力云圖Fig. 12 Simulation results stress cloud of the four kinds of improved schemes

為了對比分析本文對舷側大開口板架模型所采用的4種改進方案與未改進方案的極限承載能力，尋求最佳的改進方案。本文將原始甲板板架模型及4種優化方案的載荷位移曲線進行對比分析，如圖13所示。

對比各種方案的數值計算結果并作出分析，其對比結果如表5所示。

由表可知，與未優化的方案相比，機庫甲板板架的軸向承載能力均有所提高，但各方案的提高幅度有所不同。其中方案四結構的軸向承載能力最好，其提升幅度高達6.14%，且該方案對整體結構改變較小，重量增加只有0.33 t。因此方案四所采用的改進方案能有效地提高具有舷側大開口結構的板架模型極限承載能力，同時對整體結構的重量影響較小。

圖 13 原始甲板板架模型及4種優化方案載荷位移曲線Fig. 13 Load-displacement curves of the original model deck and different optimization scheme

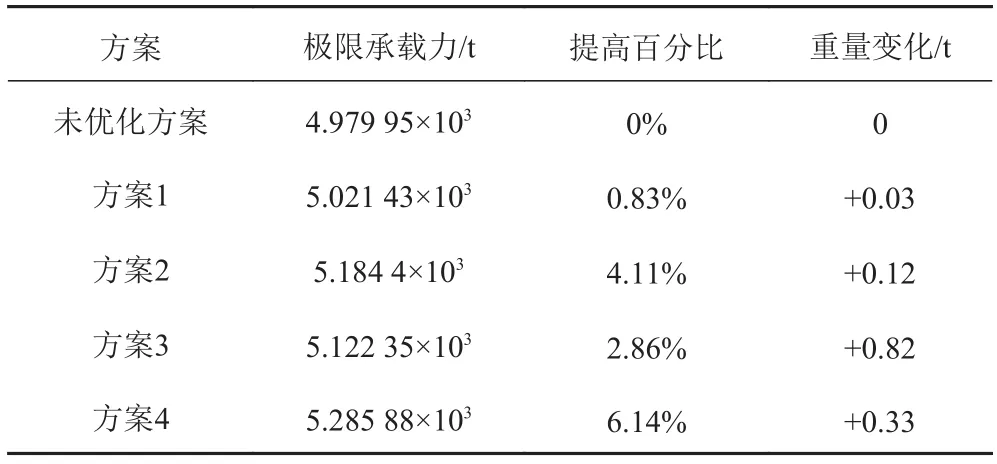
表 5 各種方案對比分析Tab. 5 Comparison of various cases

3 結 語

本文采用有限元軟件對舷側具有大開口結構的甲板板架模型進行軸壓極限承載能力的仿真計算，并開展該板架模型的模型試驗，驗證了本文所采用有限元仿真計算方法的正確性。為了提高舷側大開口板架模型的極限承載能力，采用4種改進方案，并通過這4種改進方案仿真結果的對比分析以及對具有舷側大開口結構的甲板板架模型在承受軸向壓載直至破壞詳細過程的觀測，得到以下結論：

1）非線性有限元方法能夠較為準確地模擬含有大開口的甲板板架結構的穩定性。

2）具有舷側大開口結構的甲板板架模型在承受軸向壓載的過程中，開口角隅處始終為應力集中的區域。設計過程中，應選用高強度鋼加工制造開口角隅處的甲板面板及相應的骨材。

3）在對板架結構整體結構形式及重量影響不大的前提下，增大靠近舷側大開口區域的甲板縱骨的高度，可有效地提高甲板板架的極限承載能力。