基于S函數的異步電機矢量控制仿真研究

余耀威，周少武，李蘇城

（湖南科技大學信息與電氣工程學院，湖南湘潭422201）

1 引言

三相異步電機是一個非線性、強耦合、高階次的控制對象[1]，針對異步電機的多變量數學模型人們已經進行過大量的研究，其建模方法也多種多樣，各有優缺點。傳統使用Simulink中的各個模塊來搭建異步電機模型，它簡單、直觀。但這種利用靜態建模的方法構建的模型，仿真過程中動態性能不佳，連線也比較復雜。因此，本文采取能良好適應動態仿真的S函數建立異步電機仿真模型，它與Simulink通用模塊庫的兼容性好，仿真精度也得到了提高，經過封裝后便可用于異步電機交流調速平臺中。

2 異步電機數學模型

在兩相靜止坐標系下，異步電機的狀態空間方程可描述

式 (1) 中，Usα、Usβ、Isα、Isβ、Rs、Ls分別為 αβ 坐標系下定子電壓、電流瞬時值及電阻、電感值；Irα、Irβ、Rr、Lr分別為 αβ 坐標系下轉子電流瞬時值及折算后的電阻、電感值；Lm、ωr分別為互感、轉子角速度；其中a=1/（LrLs-Lm2）

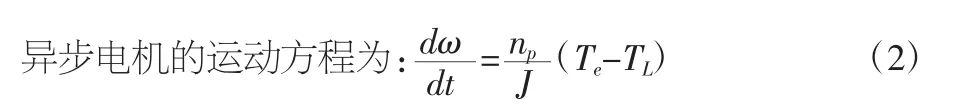
式（2）中，np、J、Te、TL分別為電機極對數、轉動慣量、電磁轉矩、負載轉矩

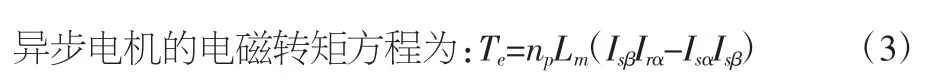
式（1）、式（2）和式（3）構成異步電機在兩相靜止坐標系下數學模型,可以看出異步電機的數學模型是一個具有多參數、強耦合的復雜系統。若采用Simulink用各個模塊搭建，必然復雜，因此有必要用S函數對其進行建模。

3 S函數的編寫與建模

MATLAB是一種交互式仿真系統[3]，其語言可按照所建立的數學模型方便表述。在Simulink工具中，利用S函數對其進行擴展，可大大減少多模塊參與連線的復雜度，方便實現仿真實驗。S函數模型用于仿真狀態空間形式的連續或離散系統的模塊，其基本格式為[4]：Function[sys,x0]=函數名(t,x,u,flag)

其中，t、x、u 分別為時間、狀態變量、輸入參量；flag 為返回變量標志。

針對前面異步電機數學模型的描述，可利用S函數對其進行封裝，如圖1所示。

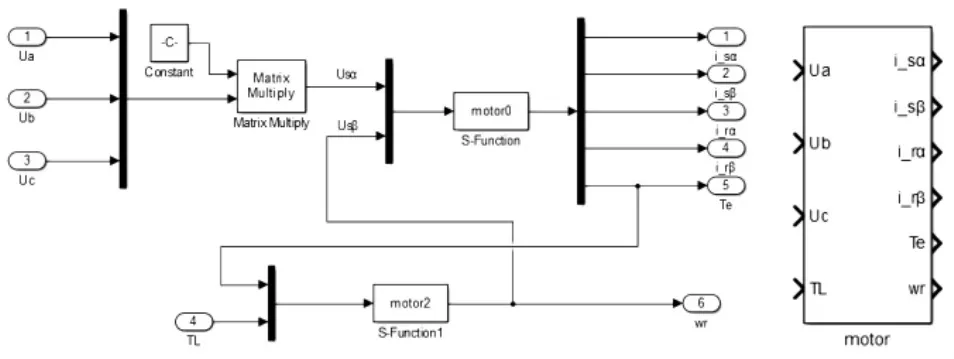
圖1 異步電機仿真模塊

由圖1可見，該模型包括兩個S函數模塊motor1(式(1)和式(3))和(motor2式(2))，下面分別對其部分子函數進行描述。

①motor1 中，根據式(1)和式(3)，可確定

S函數編寫完成后，點擊電機模型中motor1與motor2處，將其添加到S函數模塊中，并在參數欄添加所需的參數以便封裝。

4 仿真及驗證

為驗證上述模型的正確性，下面利用異步電機的矢量控制方法進行仿真。三相異步電機的矢量控制技術就是以異步電機的動態數學模型為基礎，把電機定子上的電流矢量分解成勵磁電流矢量和轉矩電流矢量，并分別控制其大小和方向,使其合并成逆變器可控的有效信號[5]。異步電機矢量控制的原理圖如圖2所示。

由圖2可知，矢量控制包括轉速PI調節器、磁鏈PI調節器、坐標變換模塊、空間矢量脈寬調制（SVPWM）、磁鏈計算等模塊，這些模塊均可使用S函數來實現。

在Simulink中將各模塊連接后，設置電機參數：額定功率Pw=1.7KW，Rs=4.1Ω，Rr=2.5Ω，Ls=0.545H，Lr=0.553H，Lm=0.510H，J=0.02kg*m2，np=2。仿真時采用 ode23tb 算法，可變步長，仿真時間是1.0s。仿真結果如下：

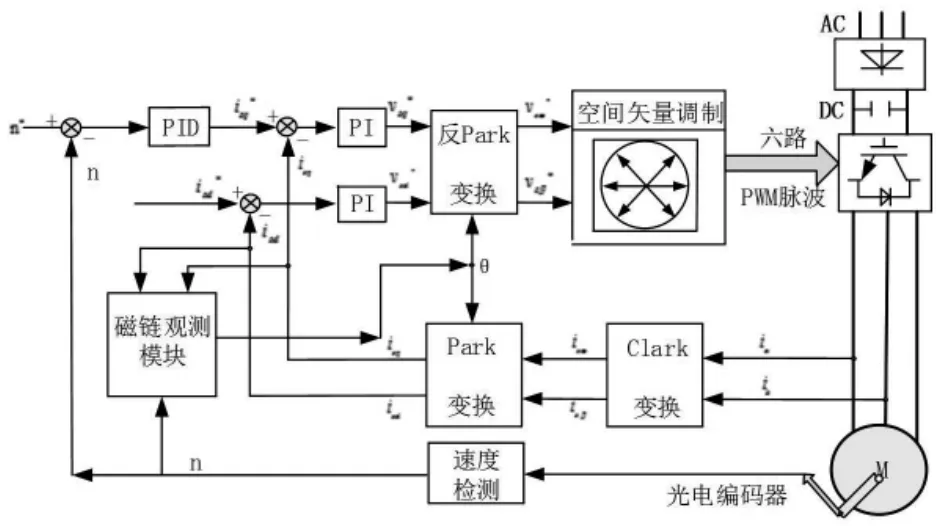
圖2 矢量控制的原理圖

①空載情況下，轉速參考值nr=1500r/min時，電機的定子電流、電磁轉矩及轉速的仿真結果如圖3。②轉速參考值=1500r/min情況下，0～0.5s內空載，0.5s時突加負載 TL=20N*m，電機的轉速的仿真結果如圖4。

從仿真實驗可以看出,異步電動機仿真模型靜態性能穩定，在0.15s內便可達到穩定狀態；在突加負載后，也能在極短的時間內重新達到平衡狀態，說明其動態響應快，故該模型仿真結果與理論分析相一致。

5 結語

本文根據異步電機在兩相靜止坐標系下的數學模型，在MATLAB環境下用S函數建立了電機模型，經過對異步電機矢量控制的仿真實驗，證明了該模塊的動靜態性能良好。由于該模塊簡單方便，擴展性強，故可用于交流調速系統仿真研究中。

圖3 空載仿真圖

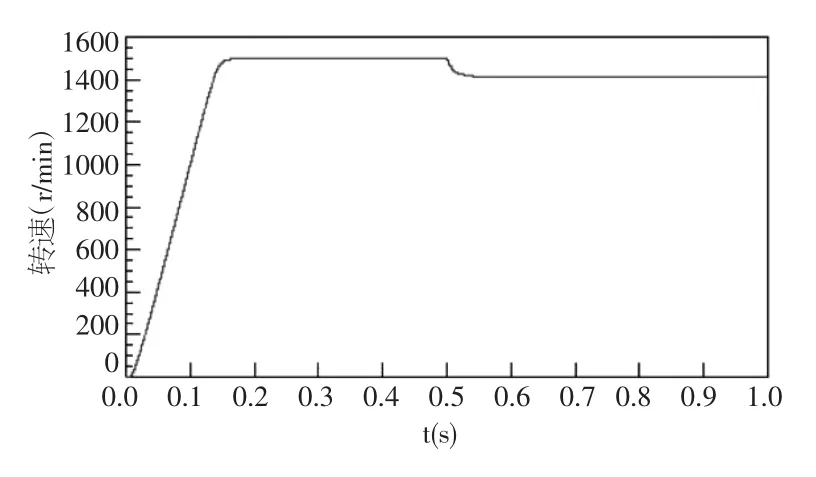
圖4 突加負載仿真圖