三角變換、三角函數及解三角形的經典題型剖析

■山東省臨沂第四中學 李新生 曹 偉

高考對三角主要是圍繞三角變換中的“變角、變名稱、變結構”和“三角函數圖像的性質及應用”，以及“三角形中的最值及范圍”等知識進行考查的，彰顯“等價轉化、整體變量和數形結合”等核心素養的具體應用。

一、三角恒等變換

1.化簡求值。

提煉：解決化簡求值問題，大多數是“切化弦通分利用輔助角公式約項或消項”，其實質是兩角和與差公式的逆用，注意式子的結構特征要和公式對應。

2.條件求值。

提煉：對于條件求值問題，實質是把所求的角用已知角進行表示，借助角的和差變換或倍半變換或互余與互補關系，有時借助換元法溝通這種關系，本題中的溝通實質是關系更加明朗化。

二、三角函數圖像的性質及應用

例3(20 18年湖南省永州市一模)已知函數f(x)=Asin(ω x+φ)，A＞0，ω＞0，

(1)求f(x)的解析式;

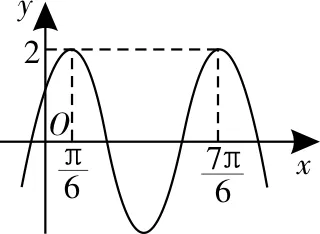
圖1

提煉：利用三角函數的對稱軸、對稱中心及周期性，可探究等高線下的兩變量滿足的關系，可以整體求三角函數值，可以降元轉化求三角函數值，還可以簡化求解三角函數值構成的數列求和問題。

三、三角形中的三角變換

例4(20 18屆江西省k 12聯盟高三教育質量檢測)在銳角△ABC中，c=2，3a=2csinA。

(1)求角C;

(2)求△ABC的周長的最大值。

方法2:用余弦定理溝通轉化均值不等式解范圍，由余弦定理得b2=4=a2+c2-a c=(a+c)2-3a c，所以4+3a c=(a+c)2≤∈(0，+∞)，所以a+c≤4，即當三角形為正三角形時，a+c的最大值為4，即△ABC的周長的最大值為4，此時三角形為正三角形。

提煉：已知三角形的一個內角與該角所對的邊，用兩種方法可探究其周長和面積最大時為等腰三角形，當這個角為時，此三角形為正三角形，對于選擇題和填空題可用此結論簡化求解。