運用平面向量解決解析幾何問題
■江蘇省鎮江第一中學 張弘毅
平面向量具有代數形式和幾何形式的“雙重身份”,能融數形于一體。解析幾何中的有些問題用常規方法去解決往往運算比較繁雜,筆者發現運用向量進行形與數的轉化,則會大大簡化解題過程,為我們提供了一種創造性的解題方法。下面就學習過程中的點滴體會與大家分享,希望對大家有所啟發,能起到拋磚引玉的作用
一、巧妙運用向量垂直的充要條件,輕松化解解析幾何中的垂直問題
解析幾何中的垂直往往利用直線斜率來處理,可由于直線位置的特殊性,使得解題過程不完備,運用向量垂直可以避開這個問題。利用a⊥b?a·b=0,可以解決垂直問題。

二、巧妙運用向量平行的充要條件,靈活轉換解析幾何中的平行或共線問題
已知a,b為非零向量,則a∥b?a=λ b(λ≠0),利用向量平行可以將解析幾何中的平行或者共線問題代數化,從而加以解決。
(1)求橢圓C的方程。

圖1
(2)過點Q(-4,0)任作一動直線l交橢圓C于M,N兩點,在線段MN上取一點R,時,點R是否在某一定直線上運動?若在,請求出該定直線;若不在,請說明理由。
解析:(1)已知△F1A F2是邊長為2的正三角形,則c=1,a=2,故橢圓C的方程為
(2)直線MN的斜率必存在,設其直線方程 為y=k(x+4),并 設 M(x1,y1),N(x2,y2)。

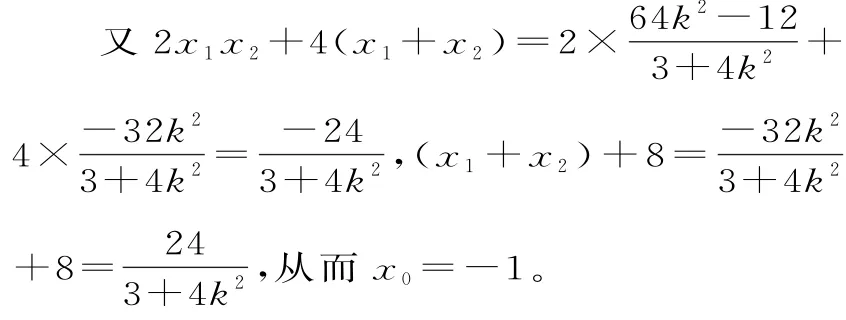
故點R在定直線x=-1上運動。
總結:向量相等的充要條件是解題的關鍵,同時要注意設而不求技巧的運用。
三、充分借助向量的工具性,巧妙求解解析幾何的綜合題
以平面向量為載體的解析幾何問題往往和向量、方程、不等式等知識聯系在一起,解決這類問題的一般方法是利用平面向量的坐標表示方法,將問題中幾何或向量關系,通過向量相關的運算性質轉換成代數關系,即代數問題,利用解析幾何的基礎知識和方法求解。通常在這些試題中向量只是個殼,一些知識點如相等、垂直、平行等借助這個殼,以解析幾何為知識載體,向量為工具,來考查我們分析問題與解決問題的能力。


總結:通觀全題的解題思路,應該說解法還是常規的,在平時的學習中要注重通法。也就是說看到題目之后,就應該明確怎樣往下走。對于這個條件,當然可以換另外一種表述方式,這里使用向量來表達此條件,其實是告訴我們向量在這里只是一種工具而已,而我們所要做的就是借助向量這個工具去解決問題。

