修正組件結構參數對旋轉穩定彈道修正彈穩定性的影響研究

王鈺， 于紀言， 王曉鳴， 馮斌

(南京理工大學 智能彈藥技術國防重點學科實驗室， 江蘇 南京 210094)

0 引言

低附帶殺傷、高打擊精度武器裝備在現代與未來戰場越來越重要，為實現旋轉穩定彈丸的高精度打擊并充分利用庫存，固定鴨翼式減旋修正組件方案應運而生[1]。

Costello等[2]、常思江等[3]和許諾等[4]建立了雙旋七自由度彈道動力學模型，并使用線性化彈道理論分別推導了平直彈道、彎曲彈道下的修正彈丸旋轉穩定性與動態穩定特性。Ollerenshaw等[5]、 Fresconi等[6]和Chang[7]分析了旋轉穩定彈丸在頭部控制力作用下的動態響應與轉彎響應相位。Wernert[8]使用線性化理論分析了鴨翼修正雙旋彈丸的俯仰、偏航角運動。文獻[9-10]使用線性化理論與赫爾維茲穩定性理論推導了含重力情況下的飛行穩定性判據。

徐敏等[11]根據細長體理論、升力面理論等建立了簡化的、不同情況下的彈- 翼組合體氣動特性，并通過數值仿真和實驗方法擬合出相關氣動特性的工程計算模型。針對鴨翼結構的旋轉彈丸氣動特性問題，許巍等[12]、朱少雄等[13]、程杰等[14-16]和張蛟龍[17]對固定鴨翼式雙旋彈丸的氣動特性進行了仿真和風洞試驗分析。

綜上所述，國內外學者已經對控制力作用下旋轉穩定彈丸的穩定性問題進行了定性或定量的建模分析，但這些模型都是基于固定的組件結構與彈丸參數，關于彈體平臺、修正組件的結構參數對彈丸飛行穩定性影響的研究較少，難以支撐雙旋修正組件優化設計與多種彈丸平臺適配性設計的需要。為了對多種彈丸平臺下的修正組件適配性與優化設計提供參考，本文結合修正組件結構與質量分布參數(如組件質量、質心位置、鴨翼翼展、舵偏角)對彈- 翼組合體氣動力的影響分析和控制力作用下的彈丸飛行穩定性判據，推導并分析了修正組件結構與質量分布參數對彈丸飛行穩定性的影響規律。

1 修正組件結構參數對氣動力的影響

旋轉穩定修正/制導彈丸的彈- 翼組合體模型如圖1所示。圖1中D表示翼身組合處彈體平均直徑；l表示鴨翼翼展；b、b0分別表示翼片平均弦長與根弦長；χL、χT分別表示鴨翼的前緣與后緣后掠角；GA表示彈體質心位置；GF表示修正組件質心位置；SW表示鴨翼的參考面積。為研究不同鴨翼舵偏角與翼展對彈- 翼組合體氣動參數的影響，假設：

1)彈體(除鴨翼)整體氣動外形保持不變；

2)鴨翼根弦、后掠角、翼型保持不變；

3)鴨翼的安裝位置保持不變。

由幾何關系可得，鴨翼參考面積SW與平均弦長b分別為

(1)

由組合體質量分布可得，組合體質心無量綱坐標公式為

(2)

彈- 翼組合體所受氣動力可分解為4個部分：彈體氣動力FB、翼面氣動力FW、彈體對翼面影響產生的附加氣動力(ΔFW)B、翼面對彈體影響產生的附加氣動力(ΔFB)W[2].

為方便分析修正組件結構參數對彈丸穩定性的影響，將修正彈組合體所受氣動力分解為兩個部分：單獨彈體(包含無鴨翼組件外形)所受氣動力、鴨翼引起的彈- 翼組合體氣動力(包括FW、(ΔFB)W與(ΔFW)B)，即

(3)

式中：FC表示組合體所受氣動力；δm表示舵偏角。

為簡化分析，假設彈體(包含無鴨翼組件)氣動外形與鴨翼翼型等參數保持不變，僅研究鴨翼外形參數(翼展與舵偏角)和組合體質量分布相關參數對彈丸穩定性的影響。

1.1 鴨翼對升力的影響模型

由于鴨舵厚度很薄，且旋轉穩定彈丸滿足小攻角假設，根據細長體理論，彈- 翼組合體的小擾動流場可簡化成攻角、舵偏和滾轉效應3種效應的疊加[16]。

為求解綜合考慮攻角、舵偏和滾轉效應影響下的單獨鴨翼升力，將滾轉效應分別與攻角和舵偏效應疊加，然后將兩種情況線性疊加。

1.1.1 攻角與滾轉疊加

記彈體飛行高低攻角為α，來流速度為v∞，水平攻角為β，鴨翼滾轉角度為γF，1號～4號鴨翼所受的升力分別為N1、N2、N3、N4. 僅考慮α的含滾轉小擾動分解的攻角效應模型如圖2所示，其中y軸垂直于彈軸向上，z軸指向彈尾視圖向右。

由模型可得：

鴨翼1與鴨翼3在y軸、z軸方向的升力分量分別為

(4)

鴨翼2與鴨翼4在y軸、z軸方向的升力分量分別為

(5)

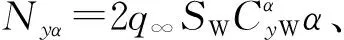
類似地，綜合考慮復攻角對流場的影響，可得復攻角效應下y軸、z軸方向的單一鴨翼升力分別為

(6)

為簡化彈、翼相互干擾升力的計算，使用氣動干擾因子與單一鴨翼升力的乘積表示干擾項。記KW(B)為攻角效應下彈體對鴨翼的氣動干擾因子，KB(W)為攻角效應下鴨翼對彈體的氣動干擾因子。由于攻角與滾轉效應引起鴨翼產生的升力(包含翼身干擾項)可表示為

(7)

1.1.2 舵偏與滾轉效應疊加

含有滾轉角小擾動分解的舵偏效應模型如圖3所示。由模型可得，舵偏效應下的4片舵合升力為

(8)

式中：δm為鴨翼舵偏角。

記kW(B)為舵偏效應下彈體對鴨翼的氣動干擾因子，kB(W)為舵偏效應下鴨翼對彈體的氣動干擾因子。在y軸、z軸方向由于舵偏與滾轉效應引起鴨翼產生的升力(包含翼身干擾項)分量可表示為

(9)

1.1.3 翼面產生的總升力

根據小擾動疊加模型，由(7)式和(9)式的線性疊加可推導出彈軸坐標系下由鴨翼產生的升力(包括鴨翼自身所受升力與鴨翼對彈體升力的影響)為

(10)

式中：FLWy、FLWz分別表示鴨翼產生的總升力在彈軸坐標系y軸、z軸方向的分量；Kαα表示攻角效應下彈頭部對鴨翼升力的干擾系數；Kδ0表示舵偏效應下彈頭部對鴨翼升力的干擾系數。

由單獨外露翼的細長體理論可得

(11)

式中：λW為外露翼展弦比，λW=(l-D)/b.

當滾轉角γp與舵偏角δm均為0時，由細長體理論分析計算獲得攻角效應模型下的Kαα[11]理論計算公式可近似為

(12)

當滾轉角與飛行攻角均為0時，理論計算的舵偏效應作用下Kδ0[11]可近似為

(13)

將(11)式～(13)式代入(10)式，可得

(14)

1.2 鴨翼對阻力的影響模型

彈- 翼組合體的阻力系數可表示為零升阻力系數(Cx0)C和升致阻力系數(Cxi)C之和：

(Cx)C=(Cx0)C+(Cxi)C.

(15)

1.2.1 零升阻力系數

對于中小展弦比的彈- 翼組合體，其零升阻力系數可表示為

(16)

式中：k1、k2為考慮翼身各部件間相互干擾引入的系數；SB和S分別表示彈體和組合體的參考面積；Cx0W、Cx0B分別表示外露翼、彈體的零升阻力系數。

根據線化理論，可得外露翼的零升阻力系數為

(17)

根據中小展弦比彈- 翼組合體的阻力特性可知，系數k1、k2僅與雷諾數、馬赫數和翼片最大厚度線后掠角相關。對于相同的彈體、相同舵形、不同舵偏角、不同翼展的彈- 翼組合體，相同飛行狀態下k1、k2相同。

綜上所述，彈- 翼組合體的零升阻力系數僅與外露翼參考面積相關，結合(1)式可知，外露翼翼展越大，組合體零升阻力系數越大。

1.2.2 升致阻力系數

組合體的升致阻力系數(Cxi)C包括：單獨彈體升致阻力系數CxiB、彈體干擾下外露翼的升致阻力系數CxiW(B)、鴨翼對彈體干擾產生的升致阻力系數CxiB(W). 由跨超音速理論可知，CxiW(B)較小，可忽略，則組合體升致阻力系數可簡化為

(18)

彈體的升致阻力系數CxiB與鴨翼結構無關，可直接由彈體的氣動仿真或試驗測試獲得。結合鴨翼產生的升力表達式(如(10)式)與升致阻力系數的定義，CxiB(W)可寫為

(19)

(20)

由(20)式可得，組合體升致阻力系數隨翼展l和舵偏角δm的增大而增大。

1.2.3 組合體阻力

綜合1.2.1節與1.2.2節的分析可知，組合體阻力可分解為彈身相關阻力與鴨翼相關阻力兩個部分：

(21)

式中：FD表示組合體阻力；FDB為彈身相關阻力，FDB只與彈體相關參數有關，不隨組件結構參數變化而變化；FDW為鴨翼相關阻力，隨鴨翼翼展變化。

1.3 鴨翼對俯仰力矩影響模型

彈- 翼組合體的俯仰力矩，即組合體法向與軸向力對組合體質心的力矩。由于旋轉穩定修正彈的軸向氣動力在不考慮制造偏心時，組合體質心和壓力中心均通過彈軸，故組合體俯仰力矩可表示為

(22)

對于旋轉穩定彈丸，飛行攻角較小，彈- 翼組合體繞組合體質心的俯仰力矩由5個部分組成：1)單獨彈體升力產生的俯仰力矩；2)單獨鴨翼升力產生的俯仰力矩；3)彈體對鴨翼干擾升力增量產生的俯仰力矩；4)鴨翼的壓強場傳遞作用引起的彈體升力變化量產生的俯仰力矩；5)鴨翼的洗流對彈體產生的力偶mzB(W). 根據上述分析，組合體俯仰力矩系數可表示為

(23)

(24)

2)相同展弦比時，舵偏角增大，鴨翼產生的俯仰力矩力臂也有一定的增加；

4)組合體質心位置越靠前，鴨翼產生的俯仰力矩力臂減小。

彈軸坐標系下組合體俯仰力矩可由(25)式計算：

(25)

2 彈- 翼組合體穩定性分析

為分析全彈(含組件)的飛行穩定性情況，從而獲得組件參數對組合體穩定性的影響規律，為組件設計提供參考，下面首先根據組合體運動模型與Murphy復攻角理論推導彈丸飛行角運動方程，然后根據Herwitz穩定性理論推導組合體飛行穩定條件。

在彈道坐標系下建立彈道方程的運動學模型，在彈軸坐標系下建立動力學模型，則包含頭部修正組件的彈丸7自由度模型，如(26)式～(28)式所示：

(26)

(27)

(28)

式中：v表示彈丸速度；m表示組合體總質量；IxA、IxF分別表示尾部和頭部的極轉動慣量；Iy表示組合體赤道轉動慣量；ψi、ψy分別表示速度傾角和速度偏角；φi、φy分別表示彈軸俯仰角和彈軸偏航角；Fxv、Fyv、Fzv表示彈體所受合外力在速度坐標系下的投影；γA、γF表示彈丸尾部和頭部的滾轉角；pA、pF表示彈丸尾部和頭部的滾轉角速度；q、r分別為俯仰角速度和偏航角速度；MAx、MFx分別表示彈軸坐標系下彈丸尾部和頭部所受力矩在彈軸上的投影；My、Mz表示彈丸總體所受合力矩在y軸和z軸上的投影；H*=pAIxA+pFIxF.

2.1 攻角方程推導

高速旋轉彈丸在飛行過程中彈軸與速度軸不重合，使用復擺動角Φ表示彈軸的空間方位，復偏角Ψ表示速度方向[18]。攻角定義為彈軸與速度軸的夾角，故有Δ=Φ-Ψ.

假設彈丸在飛行過程中滿足小攻角假設，引入只考慮阻力和重力的理想彈道模型，此時彈道傾角表示為θi. 基于上述假設，將阻力、重力以外的其他因素均視作彈道擾動，可得7自由度彈道模型中速度高低角ψi=θi+ψp，彈軸高低角φi=θi+φp，且φp、φy、ψp、ψy、δp、δy均為小量，其中δp、δy分別表示俯仰、偏航方向的攻角值。

將(26)式～(28)式代入理想彈道模型，并略去高階小量，可得復偏角方程、復擺動方程分別為

(29)

(30)

(31)

2.2 穩定性判據推導

求解攻角方程(31)式可得彈丸飛行攻角為

Δ=C1eλS+iφ′Ss+C2eλF+iφ′Fs+ΔB，

(32)

當鴨翼轉速不為0時，攻角方程的解為快圓、慢圓和控制相關的周期性強迫干擾疊加的3圓運動，則(32)式可寫為

Δ=C1eλS+iφ′Ss+C2eλF+iφ′Fs+C3eipFs+ΔBG，

(33)

當鴨翼轉速為0時，控制項為常量，相當于在攻角方程中添加了常值強迫項，則攻角運動的解可寫為

Δ=C1eλS+iφ′Ss+C2eλF+iφ′Fs+ΔBC+ΔBG，

(34)

式中：ΔBC為控制常值強迫項。攻角方程的解為快圓、慢圓運動在常值項附近的波動疊加。當λS與λF為負時，波動項隨時間收斂，彈丸角運動穩定；反之攻角隨時間發散，彈丸失穩。雖然穩定的控制力為常值項，但當飛行時突然施加階躍激勵后，攻角通常會出現較大峰值。飛行穩定性設計中，需將最大攻角幅值限定在一定范圍，參考文獻[21]可知，最大攻角值可表示為

(35)

由穩定性分析可知，當(32)式中指數λS與λF均為負，且最大攻角小于最大允許攻角δmax時，彈丸飛行具有穩定性，故可得彈丸飛行穩定性的條件為

(36)

此判據形式與傳統彈丸的穩定性判據類似，但其中參數M、P、H、T中添加了鴨翼對氣動力的影響部分。將(36)式中代入M、P、H、T表達式，并整理后可得與鴨翼引起的氣動參數相關的穩定性判據為

(37)

2.3 組件參數對穩定性的影響

將(14)式、(21)式代入x1、x2的表達式，并略去攻角相關的小量可得：

(38)

結合穩定判據(37)式與質心、壓力中心變化公式(2)式、(24)式可得：

因此，為了在增大鴨翼修正力的同時盡量保證彈體飛行穩定性，應優先選擇增大舵偏角的方案。為保證彈丸射擊初始參量(如初速等)和存速能力，組件質量不可隨意增加，故對于穩定性不佳的彈丸而言，為保證飛行穩定性，可通過彈體配重方式使彈體質心略微前移。

3 仿真與試驗

為定性地驗證上述結論的正確性，分別計算107 mm火箭炮平臺下不同翼展、不同舵偏、不同組件質心位置下的彈丸飛行穩定性情況，并通過飛行試驗對比不同翼展、不同質心位置下的彈丸無控飛行下的穩定性情況。

3.1 仿真驗證

使用滑移網格方法建立含有修正組件的彈- 翼組合體相對滾轉模型，并使用計算流體力學軟件Fluent對進行組合體流場仿真分析，從而獲取不同翼展長、舵偏角、組件質心位置的組合體氣動力(矩)參數，進而求解相同射擊諸元下的組合體飛行攻角曲線。不同情況下的組合體結構參數設置如表1所示。

表1 組合體結構參數表

分別計算不同參數下初速為500 m/s、初始轉速為25 000 r/min、47°射角條件下，20 s起控，鴨翼控制角度γp=180°時的有控彈道，不同組合體對應的時間- 總攻角圖如圖4所示，42～52 s時段內不同組合體的復攻角(α-β)圖如圖5所示。為比較1號與2號組合體的穩定性，統計45～52 s總攻角的攻角平均發散速度(即該時間段內每個波動周期攻角波動幅值相對增大量的平均值)如表2所示。

表2 攻角發散速度

由圖4、圖5與表2可知：1號、2號組合體飛行40 s后出現攻角發散現象，且1號組合體的發散速度大于2號；3號、4號組合體幾乎保持攻角波動幅值不變，且4號組合體的攻角波動幅值明顯大于3號。對比1號、2號組合體的飛行狀態可知，當其余參數相同時，組合體質心位置減小，彈體穩定性增強；對比2號、3號組合體飛行狀態可知，當其他參數均相同時，鴨翼翼展減小，彈體穩定性增強；對比3號、4號組合體的飛行狀態可知，當其余參數一致時，鴨翼舵偏角增大，對彈體穩定性幾乎沒有影響。

3.2 試驗

由于試驗硬件條件限制，未能測量彈丸飛行過程中的角運動參量，僅使用雷達測試彈道位置與速度數據。分別對表1中1號、2號、3號組合體進行飛行試驗，主動段最大速度500 m/s，射角47°，控制狀態相同，不同組合體的微波雷達測量速度如圖6所示。

由圖6可知，3條彈道的初始速度相同，在35 s之前，1號與2號組合體的速度曲線很接近，3號組合體的速度大于1號與2號；1號組合體在約35 s時阻力突然增大，速度突然下降；類似地，2號組合體在約43 s時出現失速現象；3號組合體全彈道過程中飛行速度變化規律正常。由于組合體零升阻力不可能出現突變，組合體的阻力突增、速度陡降是因為攻角增大、發散引起的升致阻力陡增。綜上所述，相同彈道條件下，1號與2號組合體均出現明顯失穩現象，且1號的穩定性劣于2號；3號組合體穩定性狀態較好。試驗結果與理論和仿真分析結果一致。

4 結論

本文在彈- 翼組合體氣動特性理論分析與工程計算方法的基礎上，將組合體主要的氣動力(矩)近似表示為彈體相關項與彈翼相關項。根據組合體動力學建模、復攻角理論與Herwitz穩定性理論，推導出包含修正組件結構參數的彈丸穩定性判據，并進一步獲得組合體結構參數對彈丸穩定性的影響規律如下：

1)當其余參數相同時，翼展越大、舵偏角增大、組合體質心越接近彈尾，修正彈丸飛行穩定性越差。

2)翼展變化對彈丸穩定性的影響明顯大于舵偏角變化對彈丸穩定性的影響。當需要增大鴨翼修正力，并同時保證彈體飛行穩定性時，應優先使用增大舵偏角的方案。

3)為保證彈丸射擊初始參量(如初速等)和存速能力，組件質量不可隨意增加，故對于穩定性不佳的彈丸而言，為保證飛行穩定性，可通過彈體配重方式使彈體質心略微前移；若彈體無法進行配重，則為了優化修正彈丸穩定性，在外形結構不變的條件下，組件質心應盡量前移。

上述分析與結論對修正組件設計與優化，尤其是多平臺適配組件的設計有一定的參考意義。