數學建模在生活應用中的探究

許亞鵬

（山西職業技術學院 山西 太原 030006）

1 引言

數學建模是指通過數學的方法和工具，對現實世界的一個特定對象，依據其內在的規律，作出一些必要的簡化假設后，從而建立一個數學結構的過程。人類在很早以前，就開始用數學去解決天文、農業生產中的各種問題了。如今，數學建模更是人們在分析自然科學和人文社科領域中分析設計、控制預測和管理決策的重要工具。本文主要從數學建模在現實生活中應用的幾方面進行探究。

2 建立整數規劃模型分析企業用料最省問題

線性規劃模型主要用來解決在既定資源配置與利用方式下，如何使其達到最佳效果，實現資源的優化合理配置。在線性規劃模型中，有一類問題，需要變量取整數時才有意義。例如，不可分解的產品數目或只能用整數來計數的對象。

企業在生產和經營時都會考慮成本問題，在成本問題中如何使用料最省顯得尤為重要，以某個企業為例說明。某裝修公司在裝修房屋時需要重新修改水電線路，在改線路時需要7米、5米、4米長的三種規格PVC管分別至少180根、210根、160根，現購置了一批規格為16米的PVC管若干根，如何截取能使16米長PVC管的用料達到最省。

分析上述問題：首先要將16米長的PVC管截成7米、5米、4米的所有可能截取方法列舉出來，分析如表1所示。

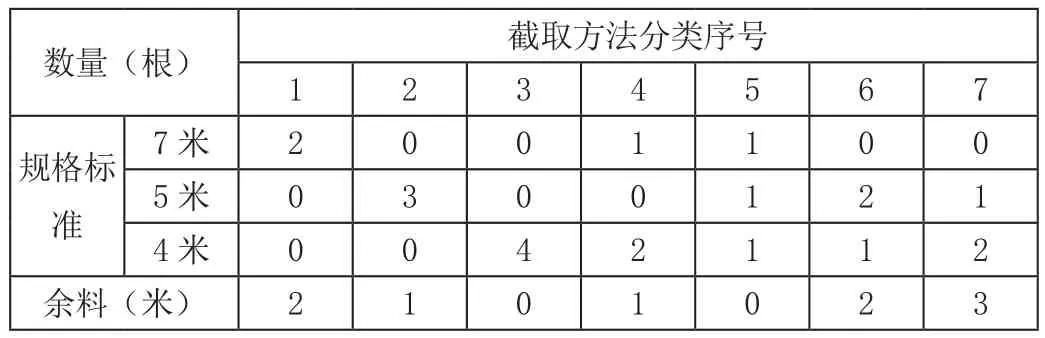
表1

然后根據上表確定決策變量：假設采用第i種截法用去16米長的PVC管χi根（i=1，2，3，4，5，6，7），最后建立如下模型：

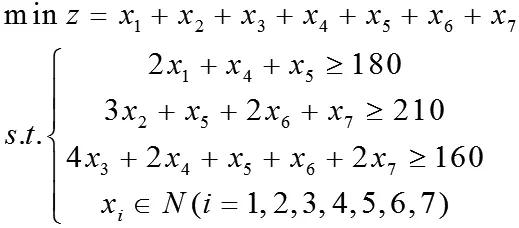
利用lingo求解模型結果。即為了滿足需7米、5米、4米長的三種規格PVC管分別至少180根、210根、160根這一要求，至少需截取16米長PVC管187根，按第一、二，五種截取方法分別截取10根、17根和160根。

3 建立指派模型合理解決工廠用人問題

某工廠引進一套新的流水生產線，這條生產線上有四個環節，各環節依次推進才能完成，現需要在這條流水線上安排合適的人選，經過對該工廠的工人進行技術培訓和幾輪技能實操比拼后留下五人，這五人各方面的條件都很優秀，可以完成任何一個職位，現擬從五人中最后選定四人并分配到合適的環節上，在最終的操作測試中，評申團為每個人在四個環節的操作上分別打分，評分如表2所示，如何合理地選擇其中四人安排在四個環節上以達到用人的最優化。

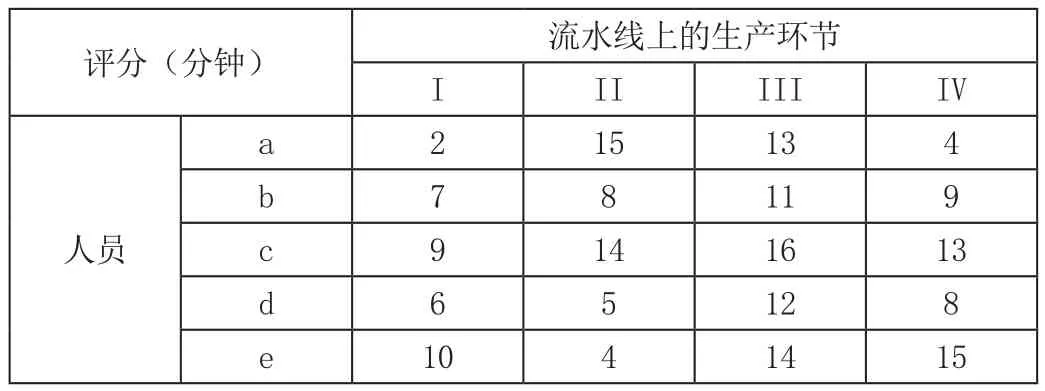
表2

問題分析：該問題屬于指派問題，指派問題需滿足n個人安排n個職務，但該問題中出現人多工作環節少的情況，不能滿足一一對應安排，因此，我們需虛擬一個工作環節，即環節V，將上述評分表修改如表3所示。

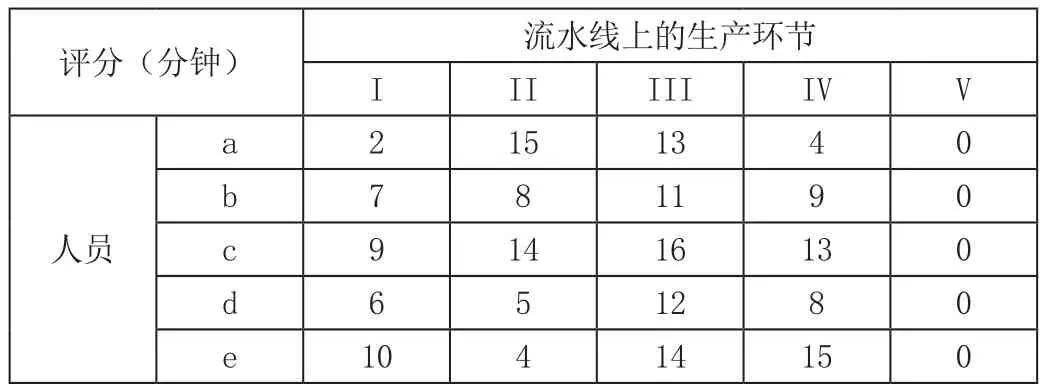
表3

（i，j=1，2，3，4，5）

然后建立這個工廠流水生產線的用人最優化的模型如下：

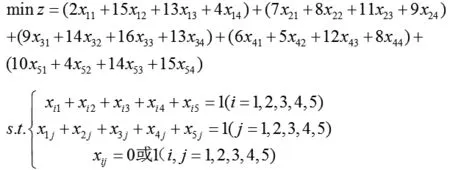
利用lingo軟件求解模型結果。第二個人被淘汰，第一個人安排在流水生產線的第四個環節，第三個人安排在流水生產線的第一個環節，第四個人安排在流水生產線的第三個環節，第五個人安排在流水生產線的第二個環節。

4 建立微分方程模型分析肇事司機醉酒駕車

微分方程模型的應用十分廣泛，在科學研究、工程技術、經濟決策中，我們經常想知道一個變量隨另一些變量的變化關系，即想找出這些一元或多元的函數關系式，然而，我們卻是知道這些函數的導數或微分所滿足的關系，從這些關系出發，把未知函數找出來的方法稱為微分方程法，即建立微分方程模型。

某城市的一條路段上發生了一起交通事故，2小時后，交警測得肇事司機血液中酒精含量為72mg/100ml，過了3小時后，交警又進行了一次酒精檢測，測得該司機血液中酒精含量為37mg/100ml。那么，事故發生時，肇事司機血液中的酒精含量為多少？

利用Matlab求解模型，模型的求解結果表明該肇事司機在事故發生時血液中的酒精濃度為107.0219mg/100ml。交通法規規定：駕駛人員血液中若每100毫升血液中酒精含量達到或超過80毫升則被定性為醉酒駕車。因此分析這起交通事故中的肇事司機屬于醉酒駕車。

論文只是列舉了數學建模在實際生活中應用的一部分，數學已滲透到生活的各個領域，生活中能用數學建模思想去解決的問題不勝枚舉。隨著傳統產業的轉型升級，隨著新知識、新技術的問世和應用，未來，數學建模必將更能為我們解決生活中的實際問題，數學建模在人類的活動中將起到更大的作用。