結構動力有限元分析中材料阻尼模型的注記

宋雪飛

上海建工集團工程研究總院 上海 201114

有限元技術在土木工程振動計算中的廣泛使用，使得結構動力建模越來越精細化，導致了自由度數目巨大的計算模型。對于大量自由度的結構動力模型，阻尼模型和參數的選取是關鍵問題之一。

基于對材料振動耗能的物理機制方面的一些試驗現象的觀察，先后提出了與速度呈線性關系的黏滯阻尼假定、與速度呈線性關系的頻率相關的黏滯阻尼假定和復阻尼假定等，這些阻尼假定和相關分析方法在文獻[1-2]中得到了比較系統的論述。但由于阻尼現象與機理的復雜性，目前尚沒有建立一般的材料阻尼理論來用于土木工程結構的動力設計。

因此建立具有理論和試驗數據基礎、適用于大規模有限元結構動力計算的阻尼理論與模型仍是一個有待解決的重要問題。

本文基于工程材料存在振動耗能常數的假定和結構動力有限元分析理論，推導出了簡單的結構材料阻尼矩陣，與構造質量矩陣和剛度矩陣的規則完全相同，便于動力有限元分析過程的實現。

同時，根據橋梁環境振動阻尼實測數據和模型橋梁阻尼的測試數據，驗證了材料振動耗能常數的存在性。振動解答比較結果表明，基于材料振動耗能常數存在假定得到的振動反應的結果與復阻尼假定下振動反應的結果在數學表達形式上相同，數值差別可以忽略不計。

1 基于有限元理論的材料阻尼模型

1.1 材料的振動衰減常數與單元阻尼矩陣

考慮慣性效應和阻尼效應的彈性介質動力平衡方程如式（1）所示[3]：

式中：A——微分算子矩陣；

σ——應力向量；

p——體力向量；

ρ——質量密度；

ü——加速度向量；

η——振動耗能常數；

式（1）對于阻尼力的處理依賴于2個假定：

1）材料振動耗能常數η存在。

2）結構阻尼力假定等于材料的振動耗能常數η與材料振動速度的乘積。

根據有限元基本原理，基于式（1）可以得到結構的動力學有限元方程〔式（2）〕：

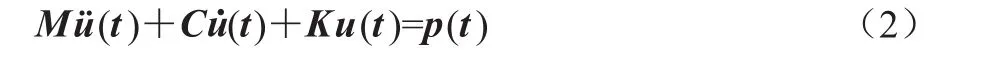
式中：M——結構質量矩陣；

C——結構阻尼矩陣；

K——結構剛度矩陣；

u——節點位移向量；

——節點加速度向量；

p(t) ——節點動力荷載向量。

基于式（1）得到的單元質量矩陣Me和單元阻尼矩陣Ce如式（3）所示：

式中：Ne——單元形函數。

由式（3）可得式（4）：

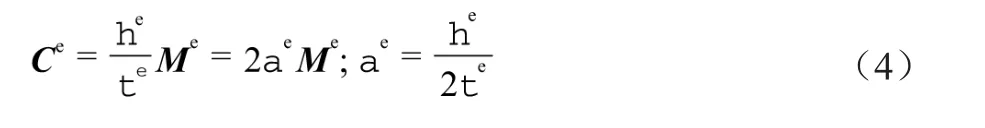
式中：αe——材料的振動衰減常數。

由式（4）可知，基于式（1）得到的單元阻尼矩陣Ce與單元質量矩陣Me成比例，比例系數為αe。當在單元層面上采用Rayleigh阻尼假定，并且只考慮質量相關項時，可以得到與式（4）相同的結果。

αe并不取決于單元材料的振動耗能常數ηe和質量密度ρe的值，而是取決于它們的比值。確切地講，αe并不是逐個單元變化的，而是因材料不同而變化的。對于單一材料構成的結構，αe對全結構取常數α，此時C=2αM，結構動力學方程（2）可以寫為：

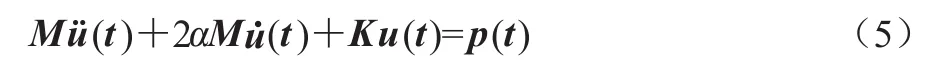
當結構不同區域由不同材料構成時，應根據不同區域確定不同的α值。此時用式（4）計算單元阻尼矩陣Ce，并根據與單元質量矩陣Me集成結構質量矩陣M相同的集成規則集成單元阻尼矩陣C。本文的討論從式（5）開始。

1.2 振型阻尼比與振型頻率之間的理論關系

記由質量矩陣M和剛度矩陣K構成的數學特征值問題所對應的特征值為ω21、ω22、…，特征向量為φ=[φ1,φ2,…]。作變換u=φx，利用φ與質量矩陣M和剛度矩陣K的加權正交關系（且φ關于質量矩陣M歸一化）可以得到：

根據黏滯阻尼假定中振型阻尼比定義，式（6）可以寫為：

比較式（6）和式（7）可知：

由于材料的振動衰減常數α僅依賴于材料特性，根據式（8），必然得到振型阻尼比ζj與振型頻率ωj的乘積為常數的結論。

1.3 阻尼比和自由振動頻率關系的試驗結果

圖1～圖3是3座大橋的振型阻尼比和振型頻率的實測結果，以及得到ζjω?j的結果。由圖可見，振型阻尼比隨振型頻率的增大呈衰減趨勢，而ζ jω?j則基本可以假定為一個常數。圖4是獵德大橋（主跨167 m＋219 m，自錨式懸索橋）幾何相似比1/50的模型在振動臺進行白噪聲激勵所識別得到的自由振動頻率和阻尼比的結果。其與前3座大橋的實測結果所反映的規律相同。

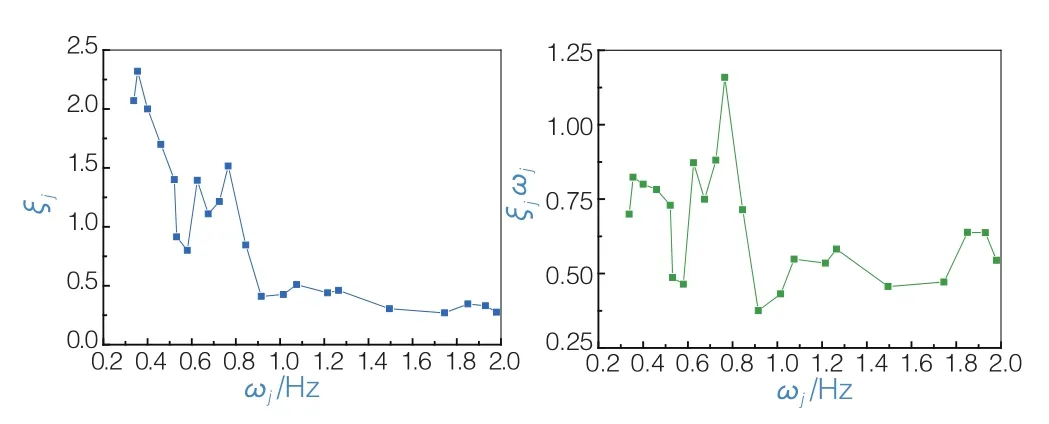
圖1 蘇通長江公路大橋振型阻尼比和自由振動頻率的實測結果

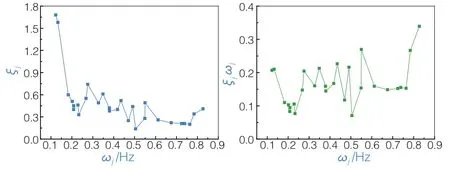
圖2 西堠門大橋振型阻尼比和自由振動頻率的實測結果

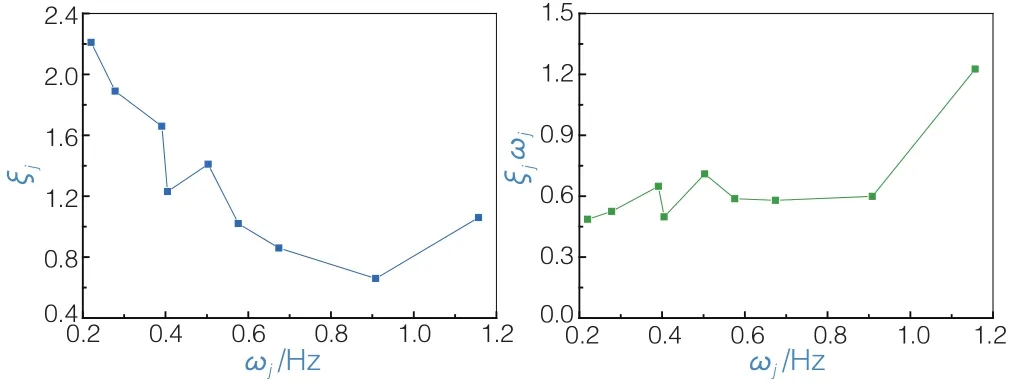
圖3 紅光大橋振型阻尼比和自由振動頻率的實測結果

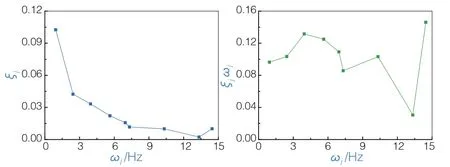
圖4 獵德大橋模型（幾何相似比：1/50）阻尼比與自由振動頻率的實測結果

可見，振型阻尼比ζj與振型頻率ωj之積為常數這一理論結果得到了橋梁原型和模型實測數據的有力支持，驗證了前述材料振動耗能常數η的存在性，表明這是材料耗能機理的一個更符合實際的描述。同時也間接支持了與速度成線性關系的黏滯阻尼假定的合理性。

上述試驗測試結果表明，通常采用的常振型阻尼比假定缺少試驗測試數據的支持，不是一個合理的假定，特別是對具有大量動力自由度的結構進行有限元計算時。試驗結果也輔證了前面數字解答的結論。

2 復雜結構情況

多數土木工程結構是一個復雜體系，耗能機制十分復雜，可分為材料阻尼、節點阻尼和界面阻尼。僅就材料阻尼而言，由于結構的不同部分由不同材料制作，因此材料耗能常數η和振動衰減常數α對于結構不同部分一般不同，也就是說不能針對全結構取相同的α。在這種情況下，結構的振動方程不能寫為式（5），而只能寫為式（2）。

在結構動力有限元建模中，如果不考慮非線性問題，結構的節點阻尼、界面阻尼以及人工阻尼一般可以描述為集中參數的黏滯阻尼。這樣在形成結構體系的材料阻尼矩陣后，可以將其他阻尼作為集中阻尼，按照動力有限元總體阻尼矩陣與單元阻尼矩陣的關系，計入這些阻尼效應。

在上述復雜阻尼情況下，結構的阻尼矩陣不能通過無阻尼實振型解耦。如果仍要堅持采用向量疊加法計算結構的振動反應，則必須解算實對稱矩陣（也可以是實非對稱矩陣）的復特征值問題。關于這一問題的討論可參見文獻[4-7]。

3 結語

通過本文的研究工作，得到了以下結果和結論：

1）提出了工程材料存在振動耗能常數假定。基于此假定，在理論上證明了結構振型阻尼比和振型頻率的乘積為常數的結論，3座原型橋梁和1座模型橋梁振型阻尼比和振型頻率的實測數據驗證了上述理論結論和材料存在振動耗能常數假定的合理性。

2）基于材料存在振動耗能常數的假定，給出了面向大量自由度土木工程結構動力有限元分析的阻尼矩陣構造方法，其規則與構造質量矩陣和剛度矩陣的方法相同，便于動力有限元方法的軟件實現。

3）本文阻尼假定下，結構動力學方程和解答以實數表達，避免了復阻尼假定下繁瑣的復數運算。