多級加載測試路基土石混合料抗剪強度研究
秦為將
(福州市規劃設計研究院 福建福州 350000)
0 引言
在山區修筑高填公路路基時,由于其地形、地貌和地質水文條件的限制,往往采用山體開挖得到的土石混合料作為筑路材料,其具有顆粒粒度變化大、含水率不均勻的特點,較難以統一控制[1]。相對于低路基,高填路基中土石混合料處于高應力狀態,若其抗剪強度不足,容易導致路基沉陷或坍塌,使路面結構過早破壞,造成較大的經濟損失。因此,抗剪強度是衡量土石混合料工程性質優劣的重要指標[2-3]。
土石混合料通常含有礫粒、卵石或巖塊,考慮到粒徑效應,對土石混合料開展抗剪強度測試往往需要采用大型三軸試驗儀進行[4]。對此,國內學者已經陸續開展了一些相關的研究。韓世蓮[5]通過大型三軸試驗發現,土石混合料的抗剪強度主要取決于顆粒之間克服咬合作用相對位移時的摩擦阻力,此阻力受到顆粒大小、級配、壓實度和應力水平的綜合影響。陸建明[6]研究了土石混合料抗剪強度的影響因素,指出顆粒破碎與粗粒含量是最主要的影響因數,含水率對抗剪強度影響不大。王冠[7]認為,土石混合料的抗剪強度主要由顆粒間粘結強度以及顆粒本身的特性決定,土顆粒的水穩定性越好,水對抗剪強度的劣化作用越弱。王星宇[8]系統研究了土石混合料的應力—應變關系,指出高壓實度、高圍壓易導致的剪脹效應,而低壓實度、低圍壓易導致剪縮效應。
以往對土石混合料開展的三軸抗剪強度試驗往往采用單級加載方式,即每更換一種應力加載方式需要采用新的試樣,最終通過對一系列平行試樣(通常為3個)在不同應力水平下的應力—應變關系,得出試樣破壞的強度包絡線,從而獲取抗剪強度參數。然而,一般大型三軸試驗的土石混合料試樣尺寸為300mm×600mm(直徑×高度),需要的備料多,壓實、脫模等過程較為麻煩,且飽和、固結所耗費的時間也遠遠大于普通的小型三軸試驗。此外,各個平行試樣壓實度、含水率、初始結構的相似性很難得到保障,容易出現較大的離散性,有時甚至采用4~5個平行試樣也很難得出合理的強度包絡線。
為解決上述問題,本文嘗試在土石混合料抗剪強度試驗中采用多級加載方式,即僅對一個試樣施加多個水平的應力(圍壓和偏應力)來獲取抗剪強度參數,以減少在單級試驗中使用多個平行試樣所產生的結果偏差,簡化試驗過程,縮短試驗周期,同時開展了采用單級加載方式的對比試驗,以驗證多級加載方式的可靠性。
1 試驗材料
試驗材料取自湖南省武陵山區某高速公路路基,從兩個標段各選取了一種土石混合料(圖1)進行研究,其級配曲線如圖2所示。
根據《公路土工試驗規程》(JTG E40—2007)[8],土石混合料A包含1.7% 的粉粒和粘粒 (φ<0.075mm)、12.3% 砂粒 (0.075mm <φ<2mm)、84.5% 礫粒(2mm <φ<60mm)和1.5% 卵石(60mm <φ<200mm),最大粒徑為76.1mm,均勻系數為9.64,曲率系數為1.95;土石混合料B包含1.0%粉粒和粘粒、15.5% 砂粒、83.5%礫粒,最大粒徑Dmax為50.8mm,均勻系數為13.3,曲率系數為2.1。相對普通土質路基填料,這兩種土石混合料都具較高的最大干密度ρdmax(2.36g/cm3、2.23g/cm3)和較低的最優含水率wopt(8.3%和10.2%)。

圖1 散狀土石混合料
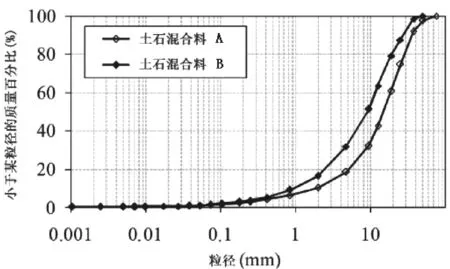
圖2 土石混合料的級配曲線
2 試驗過程
將散狀土石混合料的含水率配比至最優含水率,在金屬分裂模中將其壓實制成圓柱體試樣(圖3),尺寸為300mm×600mm(直徑×高度),壓實度為93%,試樣的壓實分為5次,每次取等量混合料,壓實到指定高度,裝下層混合料前,用工具刮毛試樣表面,讓層與層之間緊密連接,防止試樣發生層面斷裂現象。制樣完成后,取小部分樣品進行含水率和干密度的檢驗。當檢驗值與預設值的偏差小于5%時認為制樣合格,隨后裝機(圖4)進行試驗。當需要對試樣進行飽和時,采用水頭飽和方式,使其孔隙水壓力系數B至少達到95%,此過程通常需要18h以上。表1為所有壓實試樣的物理參數和三軸試驗參數。
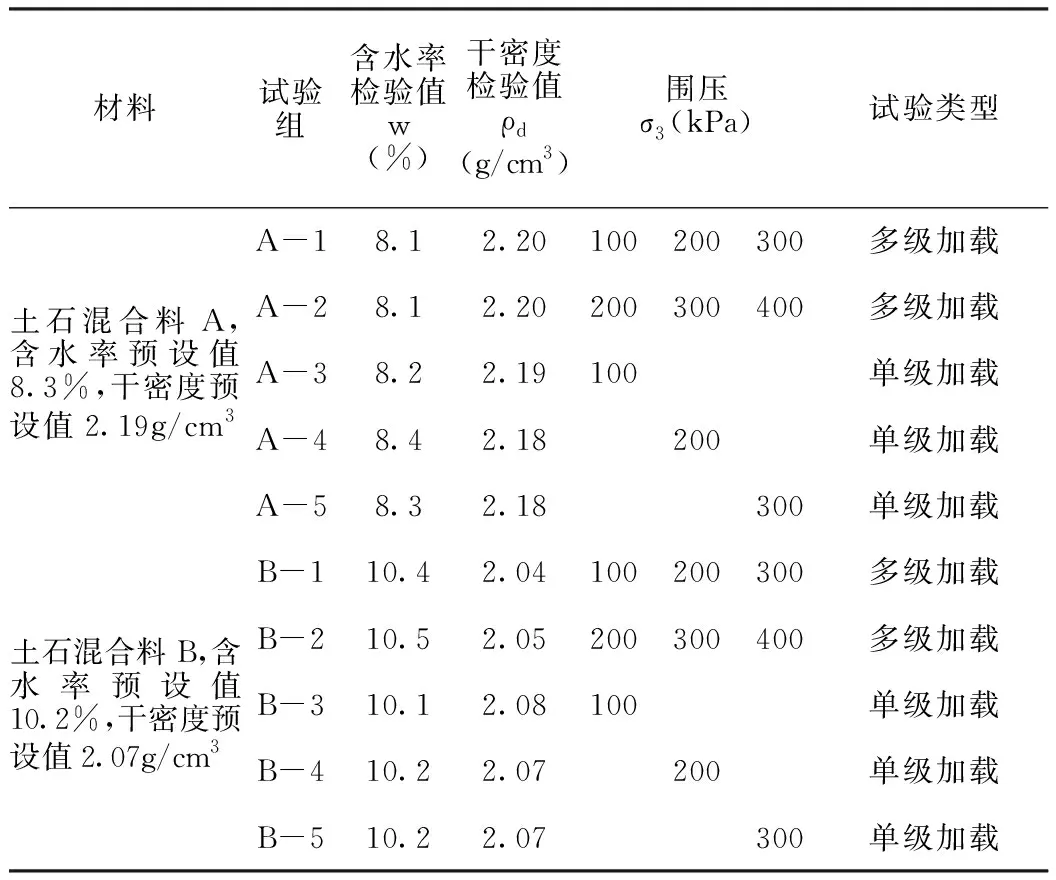
表1 試樣的物理參數和三軸試驗參數

圖3 土石混合料試樣
對于A-1和B-1,首先采用100kPa的圍壓進行等壓固結,隨后采用應變控制方式進行軸向加載,加載速率為0.03mm/min;加載時,同時打開排水閥門;當軸向偏應力出現峰值時進行卸載;隨后將圍壓分別設置為200kPa和300kPa;重復上述過程。最后,在300kPa條件下對試樣進行飽和,再進行一次加載試驗。A-2和B-2的試驗方式與上述相同,但圍壓分別為200kPa、300kPa和400kPa。對A-3~A-5和B-3~B-5進行的是單級加載試驗。試樣首先在指定的圍壓下進行等壓固結,隨后進行傳統的單級加載試驗。上述試驗方案,一方面是為了驗證多級加載試驗結果是否與單級加載試驗結果接近;另一方面,是探索由最優含水率狀態進入飽和狀態時,土石混合料的抗剪強度是否會發生較大變化,從而評價土石混合料的水穩定性。

圖4 大型三軸試驗儀
3 試驗結果分析
3.1 應力-應變關系
圖5和圖6分別為兩種土石混合料的應力-應變曲線,其中q為軸向偏應力(q=σ1-σ3),ε1為軸向應變。可以看出,土石混合料的應力-應變關系是非線性的,第一級圍壓下試樣產生的軸向應變最大,后續各級圍壓下試樣的軸向應變大小接近;當圍壓增加時,應力峰值也會增加,試驗結果規律性較好。
當試樣飽和時,應力達到峰值后逐漸下降,應力-應變曲線屬于加工軟化型[10],圍壓越大,試樣的殘余強度越大。同一圍壓下,飽和狀態應力峰值與非飽和狀態應力峰值接近,含水率對混合料的應力-應變行為影響不大。這可能是兩種土石混合料的細粒(d<0.075mm)含量較小所致(均小于2%),可見兩種土石混合料的水穩定性較好。
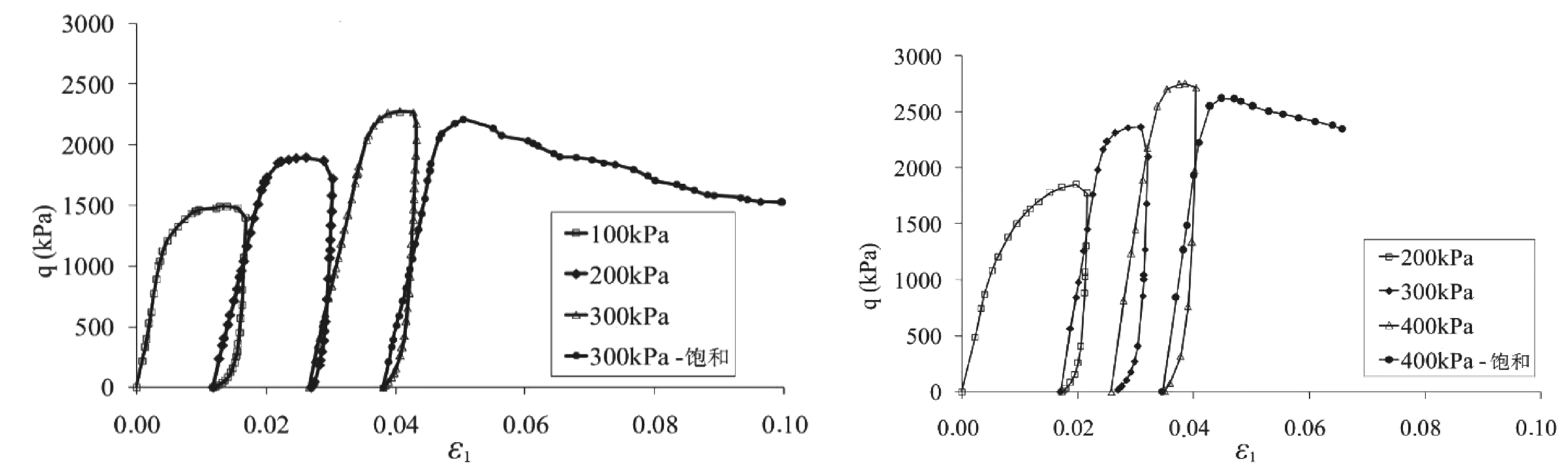
圖5 各圍壓下多級加載試驗的應力-應變關系(土石混合料A)
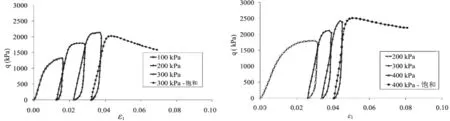
圖6 各圍壓下多級加載試驗的應力-應變關系(土石混合料B)
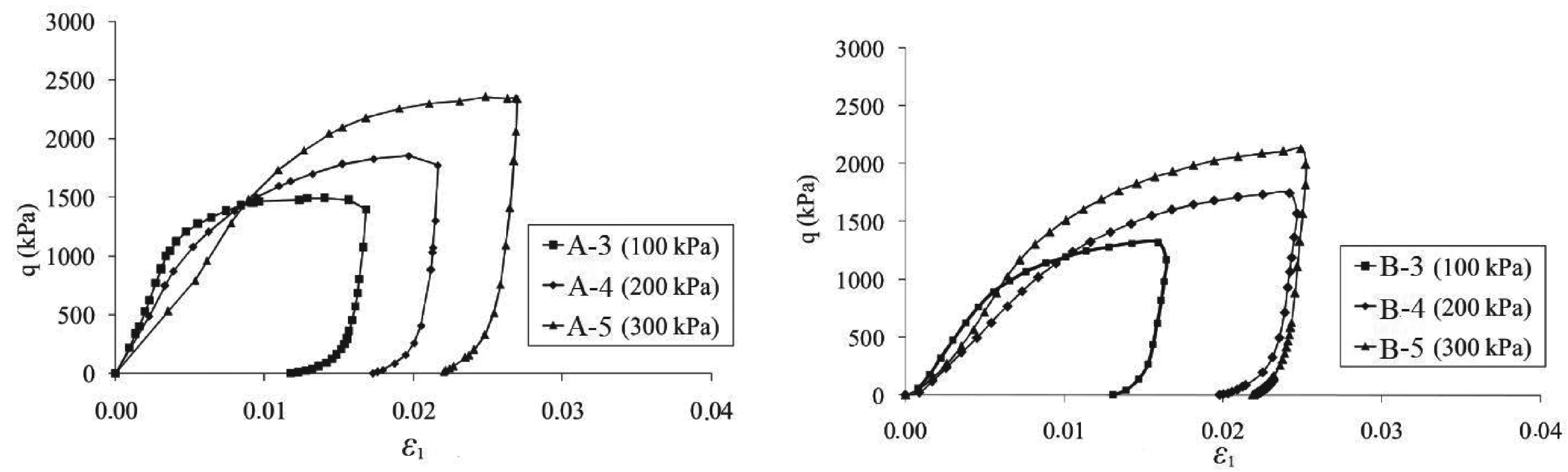
(a)土石混合料A (b)土石混合料B圖7 單級加載試驗的應力-應變關系
圖7為單級三軸試驗試樣的應力—應變曲線。可見圍壓越大,產生的豎向應變越大。值得注意的是,從圖7(b)可以看出,盡管B-4和B-5兩個試樣的偏應力峰值有明顯差異,但兩者產生的軸向應變十分接近,這可能是兩個平行試樣的差異性較大所致。
3.2 多級加載下強度包絡線分析
多級加載三軸試驗中,試樣在施加I級應力(含圍壓和軸向應力)而達到破壞后,相應的莫爾圓如圖8中的①圓,它與強度包絡線相切于P點,相應于P點的正應力為σI,剪應力為ηI,此時可得:
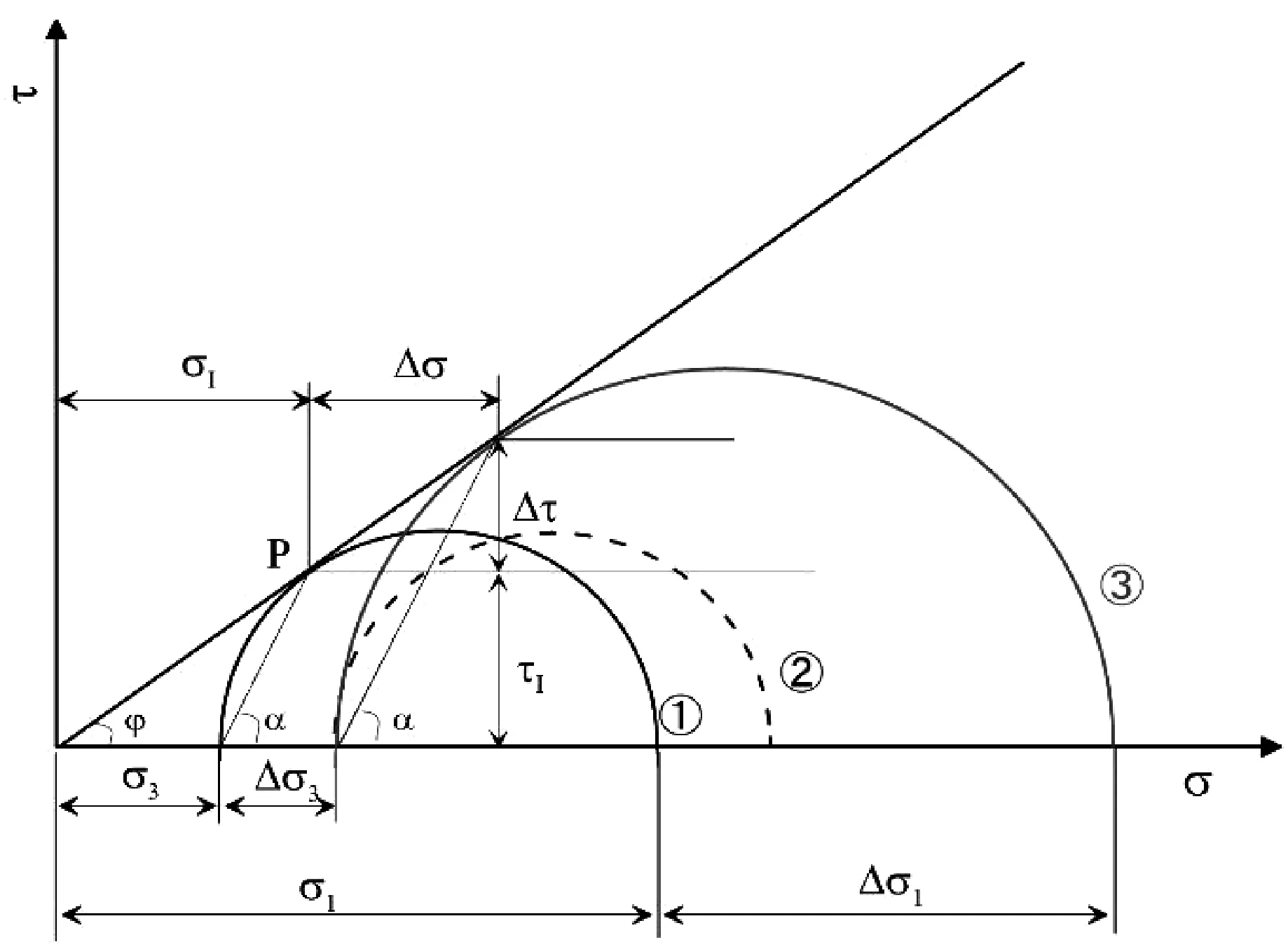
圖8 多級加載下試樣的應力莫爾圓
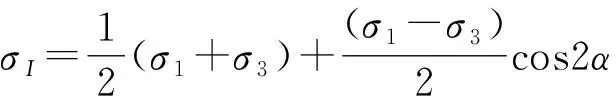
(1)
(2)
破壞面的傾角α=(45°+φ/2)在以后各級應力下均保持不變。對處于該極限應力狀態的試樣繼續施加圍壓增量Δσ3,則圖中①圓變為處于穩定狀態的②圓,在此情況下對試樣施加軸向力使之達到極限狀態,此時的莫爾圓由②變為③,II級應力下破壞面上的正應力σII和剪應力τII分別為:
(3)
(4)
從式(3)和式(4)中分別減去式(1)和式(2),可得:
(5)
(6)
上述推導表明,對試樣施加第一級荷載后再施加第二級荷載,破壞面上正應力和剪應力的增量分別為Δσ和Δτ,由此在每一級加載下可以求出σ和τ,從而可繪制出相應的莫爾圓,并確定強度包絡線。
圖9和圖10分別為土石混合料A和B的強度包絡線。該包絡線可以采用式(7)進行表示,可以看出擬合效果較為理想。由于土石混合料屬于散粒材料,粘聚力c僅具有數學意義,因此本文不進行相關探討。土石混合料的內摩擦角φ可以通過式(8)求出。
Lp=a+sptanα
(7)
sinφ=tanα
(8)
表2總結了本試驗所得到的抗剪強度參數,其中①、②、③為多級加載試驗結果,④為單級加載試驗結果。對于土石混合料A,①、②、③與④的相對差異分別為-3.7%、-8.0%、5.9%,對于土石混合料B,①、②、③與④的相對差異分別為3.3%、-1.5%、2.8%,可見多級加載方式結果與單級加載方式結果比較接近。同時可以看出,兩種土石混合料的粒徑差異,對內摩擦角的影響參數不大,且內摩擦角普遍較高。
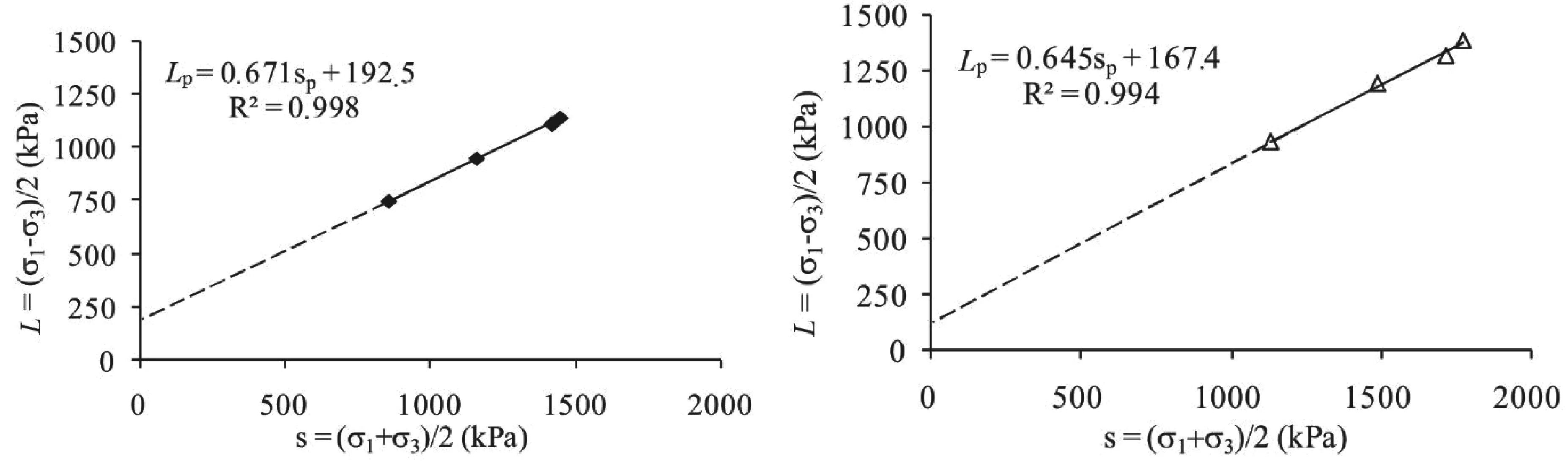
(a)A-1 (b)A-2圖9 土石混合料A的強度包絡線
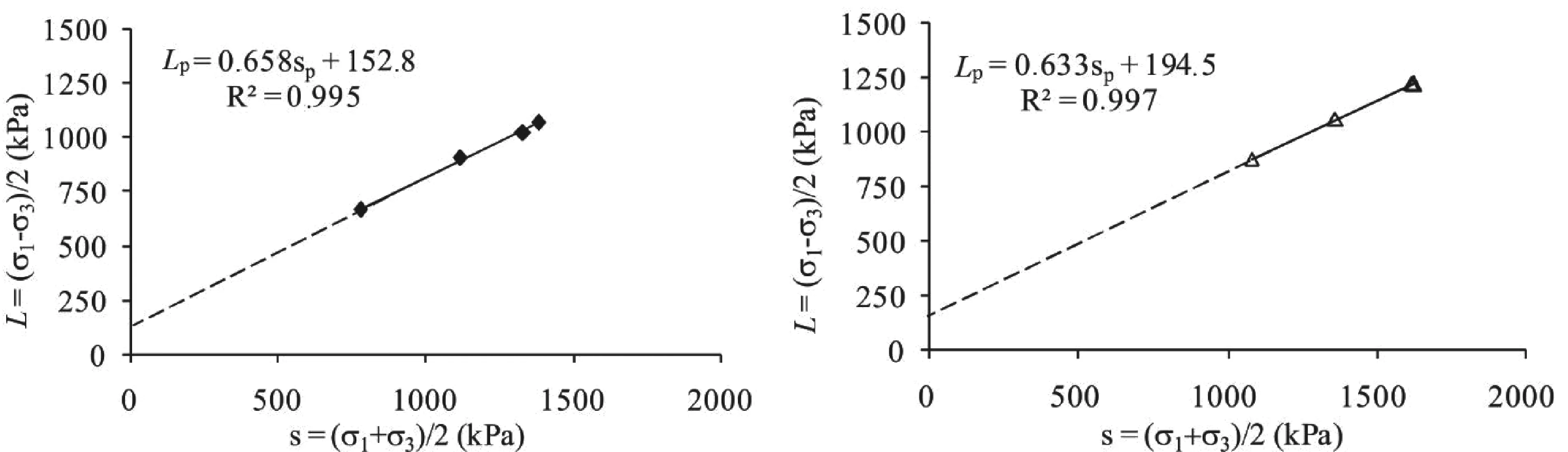
(a)B-1 (b)B-2圖10 土石混合料B的強度包絡線
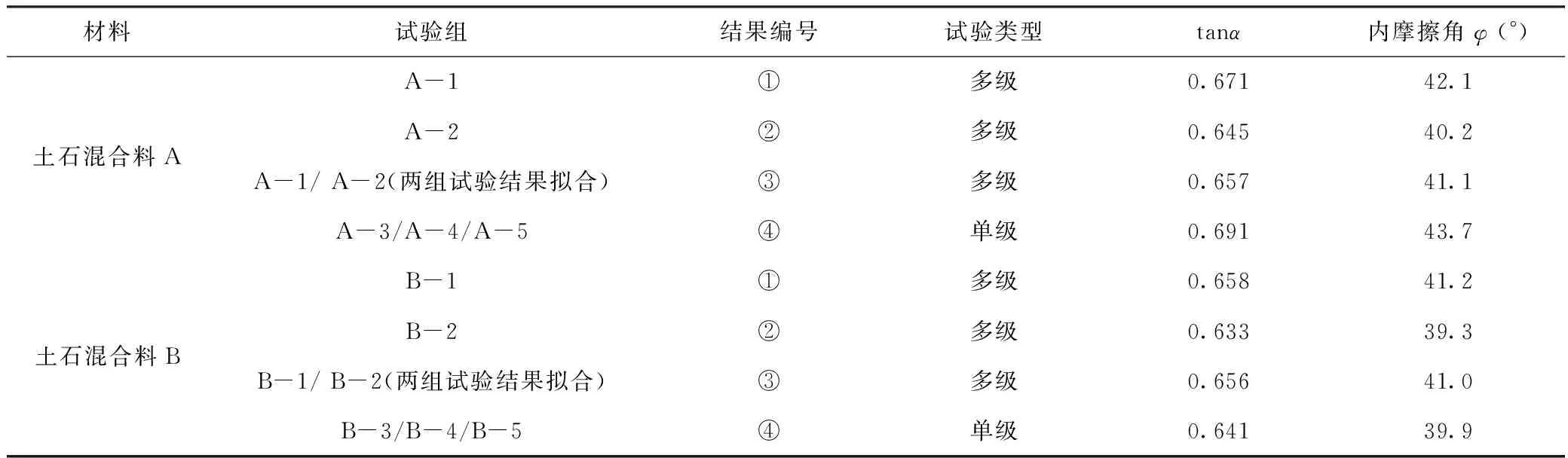
表2 多級和單級三軸試驗結果的比較
圖11為結果③與結果④的比較。結果④的強度包絡線采用了3個單級試驗的數據進行確定,結果③的強度包絡線則采用了所有多級試驗的數據進行確定。可以看出,兩者較為一致。
綜上所述,采用多級加載方式測試土石混合料的抗剪強度是可靠的,可以大大簡化試驗過程,而且對同一種類型的混合料只需要制備一個試樣,減少了制備多個平行試樣時由于試樣差異導致的結果偏差。
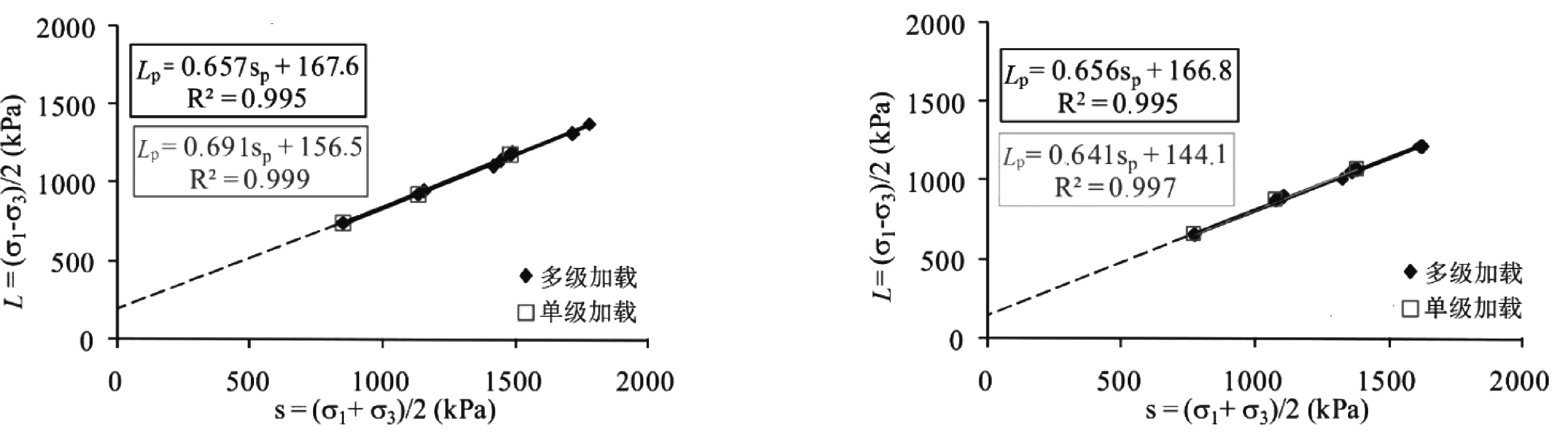
(a)土石混合料A (b)土石混合料B圖11 多級加載和單級加載試驗的強度包絡線比較
4 結論
本文探討了多級加載方式下建立強度包絡線的理論基礎。通過比較兩種不同加載方式 (多級和單級)所獲得的抗剪強度參數,驗證了采用多級加載方式測試土石混合料抗剪強度的可靠性,同時分析了抗剪強度參數與含水率的關系,得到如下結論:
(1)壓實土石混合料的應力—應變關系是非線性的。多級加載試驗中所有試樣的應力—應變關系較為規律;而在對土石混合料B的單級加載試驗中,盡管B-4和B-5兩個試樣的偏應力峰值有明顯差異,但產生的軸向應變十分接近,體現了單級加載試驗中平行試樣差異對試驗結果的影響。
(2)兩種土石混合料的抗剪強度受含水率影響較小,因而具有較好的水穩定性。這可能是由于細粒(d<0.075mm)含量較小所致。
(3)通過多級加載試驗測得的內摩擦角與單級試驗結果接近,對于土石混合料A,①、②、③與④的相對差異分別為-3.7%、-8.0%、5.9%,對于土石混合料B,①、②、③與④的相對差異分別為3.3%、-1.5%、2.8%,總體上相對差異絕對值小于8%,從而驗證了多級加載試驗的可靠性,為測試大型土石混合料試樣的抗剪強度提供了簡化、經濟的方法。

