分數(shù)導(dǎo)數(shù)Kelvin粘彈性土中管樁的扭轉(zhuǎn)振動

劉林超，閆啟方，牛潔楠

(信陽師范學(xué)院 建筑與土木工程學(xué)院，河南 信陽 464000)

樁土動力相互作用問題作為一個研究熱點得到了眾多學(xué)者的關(guān)注和重視，但無論是研究實芯樁還是管樁的振動特性，對土體本構(gòu)模型的選取十分關(guān)鍵，這關(guān)系到土體力學(xué)行為的描述與實際工況的符合程度，通常情況是將土體視為彈性或粘彈性介質(zhì)，將土體視為彈性介質(zhì)，Novak等[1]和Nogami等[2]較早地對實芯樁的振動進行了研究，王國才等[3]借助于積分方程研究了均質(zhì)彈性地基中單樁的扭轉(zhuǎn)振動問題，Lü等[4]利用Rayleigh-Love桿理論和樁土摩擦模型對層狀土中樁的縱向振動進行了研究，劉林超等[5]將樁周土、樁芯土和管樁視為軸對稱模型研究了彈性土中管樁的縱向振動，欒魯寶等[6]在考慮樁體剪切變形的情況下得到了PCC樁水平振動響應(yīng)的解析解，吳文兵等[7]采用Rayleigh-Love動力桿件模型和附加質(zhì)量模型建立了樁側(cè)土-管樁-土塞系統(tǒng)的縱向振動控制方程，同時，運用積分變換和阻抗函數(shù)傳遞技術(shù)給出了頻域內(nèi)任意荷載形式下管樁樁頂速度響應(yīng)的解析解；將土體視為粘彈性介質(zhì)，Novak[8]給出了樁基的動力剛度和阻尼，Yao等[9]研究了粘彈性Winkler地基中單樁在水平循環(huán)荷載作用下的振動問題，周緒紅等[10]在考慮軸力作用的情況下研究了粘彈性介質(zhì)中樁基的動力問題，楊驍?shù)萚11]采用三維軸對稱模型得到了粘彈性端承樁的軸對稱解析解，鄭長杰等[12-13]對單相和飽和粘彈性土中大直徑管樁的水平振動進行了研究，吳文斌等[14]利用虛土樁模型研究了均質(zhì)粘彈性地基中樁土縱向耦合振動問題。需要指出，將樁周土或樁芯土視為彈性介質(zhì)則不能考慮土體的粘性性質(zhì)，將土視為粘彈性介質(zhì)較為符合工程實際，但需選擇合理正確的土體粘彈性本構(gòu)模型。

當將樁周土或樁芯土視為粘彈性介質(zhì)時，合理的本構(gòu)關(guān)系對于土體力學(xué)行為的準確描述至關(guān)重要。目前，對于粘彈性材料應(yīng)力-應(yīng)變關(guān)系的刻畫主要是采用經(jīng)典的粘彈性模型。然而，對于經(jīng)典的粘彈性本構(gòu)模型，整數(shù)階微分算子的性質(zhì)決定其蠕變?nèi)崃亢退沙谀Ａ恳话阒荒芡ㄟ^指數(shù)函數(shù)的組合得到，且通過取消高階的微分項或者降低本構(gòu)模型的應(yīng)用范圍來精確擬合實驗數(shù)據(jù)[15]。隨著分數(shù)階微分和分數(shù)階積分的發(fā)展，借助于分數(shù)導(dǎo)數(shù)理論建立起來的分數(shù)導(dǎo)數(shù)粘彈性本構(gòu)模型由于具有確定模型需要較少的實驗參數(shù)和能在較寬的頻率范圍內(nèi)擬合材料的力學(xué)行為而得到了廣泛的應(yīng)用。將樁周土體視為粘彈性介質(zhì)并采用分數(shù)導(dǎo)數(shù)粘彈性模型來描述其應(yīng)力-應(yīng)變關(guān)系，劉林超等[16-17]、聞敏杰等[18]研究了實芯樁的水平、豎向和扭轉(zhuǎn)振動問題。本文將樁周土和樁芯土都利用分數(shù)導(dǎo)數(shù)Kelvin粘彈性本構(gòu)模型來描述，研究分數(shù)導(dǎo)數(shù)Klevin粘彈性土中管樁的扭轉(zhuǎn)振動特性。

1 數(shù)學(xué)模型與土體運動方程

圖1為粘彈性土與端承管樁的動力相互作用模型，管樁樁頂作用一集中扭轉(zhuǎn)荷載T(t)，粘彈性土層厚度和管樁長度均為H，管樁外半徑和內(nèi)半徑分別為r1和r2。為了建立管樁與粘彈性土體的動力相互作用模型，假設(shè)管樁樁芯土體和樁周土體均為粘彈性土體，且樁芯土和樁周土均與管樁完全接觸；管樁底部為基巖，管樁底端為固定端；管樁、樁周土和樁芯土均為小變形。

圖1 粘彈性土-管樁扭轉(zhuǎn)相互作用模型Fig.1 Torsional interaction model of

這里以β=1代表樁周粘彈性土體，β=2代表樁芯粘彈性土體，可以建立軸對稱坐標下樁周粘彈性土和樁芯粘彈性土的運動方程和幾何方程分別為[19]

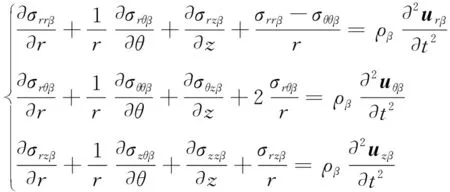
(1)

(2)

式中:σrrβ,σθθβ,σrzβ分別為粘彈性土體徑向應(yīng)力、環(huán)向應(yīng)力和剪切應(yīng)力，urβ，uθβ，uzβ分別為粘彈性土體的徑向位移、環(huán)向位移和豎向位移，ρβ為粘彈性土體的密度，uβ為粘彈性土體的位移張量。

為了更合理地考慮樁周土和樁芯土的粘彈性性質(zhì)，采用分數(shù)導(dǎo)數(shù)Kelvin粘彈性模型構(gòu)建樁周土和樁芯土的三維本構(gòu)關(guān)系，即[20]

(3)

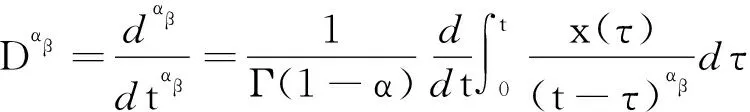
對于粘彈性土體中管樁的扭轉(zhuǎn)簡諧振動問題，為了簡化計算，這里只考慮樁周土和樁芯土的環(huán)向位移uθβ，其他位移忽略不計，在此情況下由式(1)～式(3)可以建立分數(shù)導(dǎo)數(shù)粘彈性土體以環(huán)向位移表示的樁周土和樁芯土的扭轉(zhuǎn)振動控制方程為

(4)

很明顯，式(4)即適用于分數(shù)導(dǎo)數(shù)Kelvin粘彈性土體的扭轉(zhuǎn)振動，也適用于經(jīng)典Kelvin(αβ=1)粘彈性土體以及彈性土體(aβ=bβ=0)的情形。

2 分數(shù)導(dǎo)數(shù)Kelvin粘彈性土層的扭轉(zhuǎn)振動求解

令式(4)中β=1和β=2可得分數(shù)導(dǎo)數(shù)Kelvin粘彈性樁周土和樁芯土的扭轉(zhuǎn)振動方程分別為

(5)

(6)

對方程式(5)和式(6)兩端分別進行Fourier變換可得

(7)

(8)

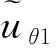
(9)

(10)

(11)

(12)

(13)

(14)

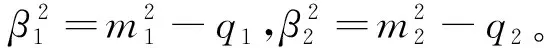
(15)

(16)

式(11)和式(14)中，I1(·)、K1(·)分別為1階第1和第2類虛宗量貝塞爾函數(shù)，A1、B1、C1、D1、A2、B2、C2、D2為待定系數(shù)。

cos(m1δ)=0，cos(m2δ)=0

(17)

由式(17)可得到

(18)

則分數(shù)導(dǎo)數(shù)Kelvin粘彈性樁周土和樁芯土的環(huán)向位移可以分別用級數(shù)表示為

(19)

(20)

式中：A2n、B2n為待定系數(shù)。考慮分數(shù)導(dǎo)數(shù)Kelvin粘彈性體本構(gòu)關(guān)系式(3)，并對其進行Fourier變換，則有

(21)

(22)

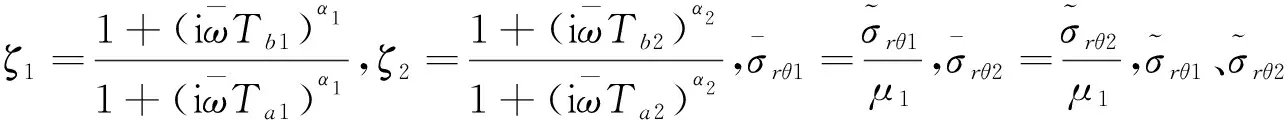
(23)

(24)

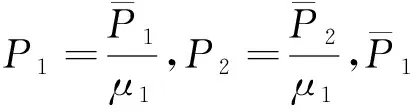
3 分數(shù)導(dǎo)數(shù)Kelvin粘彈性土端承管樁的扭轉(zhuǎn)振動求解

以管樁樁身微元作為研究對象可以建立分數(shù)導(dǎo)數(shù)Kelvin粘彈性土中管樁的扭轉(zhuǎn)振動控制方程為

(25)

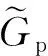
(26)

(27)

(28)

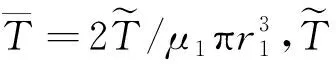
(29)

考慮管樁與樁周土和樁芯土接觸面邊界條件式(28)，由式(19)、式(20)可得

(30)

(31)

(32)

(33)

由此可得分數(shù)導(dǎo)數(shù)Kelvin粘彈性土中管樁扭轉(zhuǎn)振動的扭轉(zhuǎn)角為

(34)

進而可以得到頻率域內(nèi)分數(shù)導(dǎo)數(shù)Kelvin粘彈性土管樁樁頂?shù)呐まD(zhuǎn)復(fù)剛度

(35)

4 數(shù)值算例分析與討論

為了研究分數(shù)導(dǎo)數(shù)Kelvin粘彈性土中管樁的扭轉(zhuǎn)振動響應(yīng)特性，根據(jù)式(35)得到的管樁樁頂扭轉(zhuǎn)復(fù)剛度編寫計算程序并進行數(shù)值分析，圖2—圖11為：管樁與樁周土剪切模量比Gp=2 000，分數(shù)導(dǎo)數(shù)階數(shù)α1=α2=0.5，管樁長徑比δ=20，管樁與樁周土密度比ρp/ρ1=2.0，土體分數(shù)導(dǎo)數(shù)本構(gòu)模型參數(shù)Ta1=Ta2=2.0，Tb1=Tb2=4.0，樁芯土與樁周土剪切模量比μ=1.0，以上參量的取值是在樁身混凝土和土體實際常用參量值的基礎(chǔ)上確定的，土體分數(shù)導(dǎo)數(shù)模型參數(shù)可以通過實驗數(shù)據(jù)擬合的方法得到[22]。圖2給出了管樁扭轉(zhuǎn)振動的分數(shù)導(dǎo)數(shù)粘彈性解、經(jīng)典粘彈性解和彈性解的對比，可以看出，分數(shù)導(dǎo)數(shù)粘彈性解可退化到經(jīng)典粘彈性和彈性解的情況，間接說明采用分數(shù)導(dǎo)數(shù)粘彈性模型分析管樁扭轉(zhuǎn)振動的可行性和正確性，且彈性解的扭轉(zhuǎn)復(fù)剛度要較粘彈性解大。圖3和圖4分別給出了樁周土和樁芯土本構(gòu)關(guān)系中分數(shù)導(dǎo)數(shù)的階數(shù)α1、α2不同時對管樁扭轉(zhuǎn)復(fù)剛度的影響，可以看出，樁周土分數(shù)導(dǎo)數(shù)的階數(shù)α1對扭轉(zhuǎn)復(fù)剛度的實部和虛部的影響相對較大，且分數(shù)導(dǎo)數(shù)的階數(shù)越大，扭轉(zhuǎn)復(fù)剛度實部和虛部隨頻率變化曲線的峰值越小；而樁芯土分數(shù)導(dǎo)數(shù)的階數(shù)α2對扭轉(zhuǎn)復(fù)剛度的影響與頻率有關(guān)，頻率較低時α2幾乎沒有影響，而高頻時有一定的影響。圖5和圖6給出了參數(shù)Tb1和Tb2不同時復(fù)剛度隨頻率的變化曲線，Tb1和Tb2對扭轉(zhuǎn)復(fù)剛度的影響與分數(shù)導(dǎo)數(shù)的階數(shù)α1和α2的影響規(guī)律類似，即Tb1的影響較大且Tb1越大扭轉(zhuǎn)復(fù)剛度的實部和虛部隨頻率變化曲線的峰值越小，而Tb2的影響與頻率有關(guān)。由圖7和圖8可知，當樁芯土與樁周土剪切模量比μ大于1時，其對管樁樁頂扭轉(zhuǎn)復(fù)剛度幾乎沒有影響，這可能是因為樁芯土與管樁接觸面相對較小，導(dǎo)致增大樁芯土剪切模量時其對管樁的剪切作用力增大不明顯；當μ小于1且較小時剪切模量比對管樁復(fù)剛度有一定的影響但不是太大，但當μ較大時扭轉(zhuǎn)復(fù)剛度實部和虛部隨頻率變化曲線波動則較大。管樁壁厚對扭轉(zhuǎn)復(fù)剛度的影響較大(如圖9)，隨著樁周內(nèi)半徑的增大，即管樁壁厚的減小，扭轉(zhuǎn)復(fù)剛度實部和虛部隨頻率變化曲線峰值對應(yīng)的頻率越小，曲線波動越大。與實芯樁一樣，管樁長徑比(圖10)和管樁與土體的剪切模量比(圖11)對管樁的影響也較大，管樁長徑比越大復(fù)剛度的實部和虛部越小，樁長較長時長徑比的影響程度將減小；隨著管樁與土體剪切模量比的增大，管樁樁頂復(fù)剛度實部和虛部越大，這可能是因為管樁模量較大時管樁抗扭剛度大，管樁扭轉(zhuǎn)角小而導(dǎo)致復(fù)剛度增大。

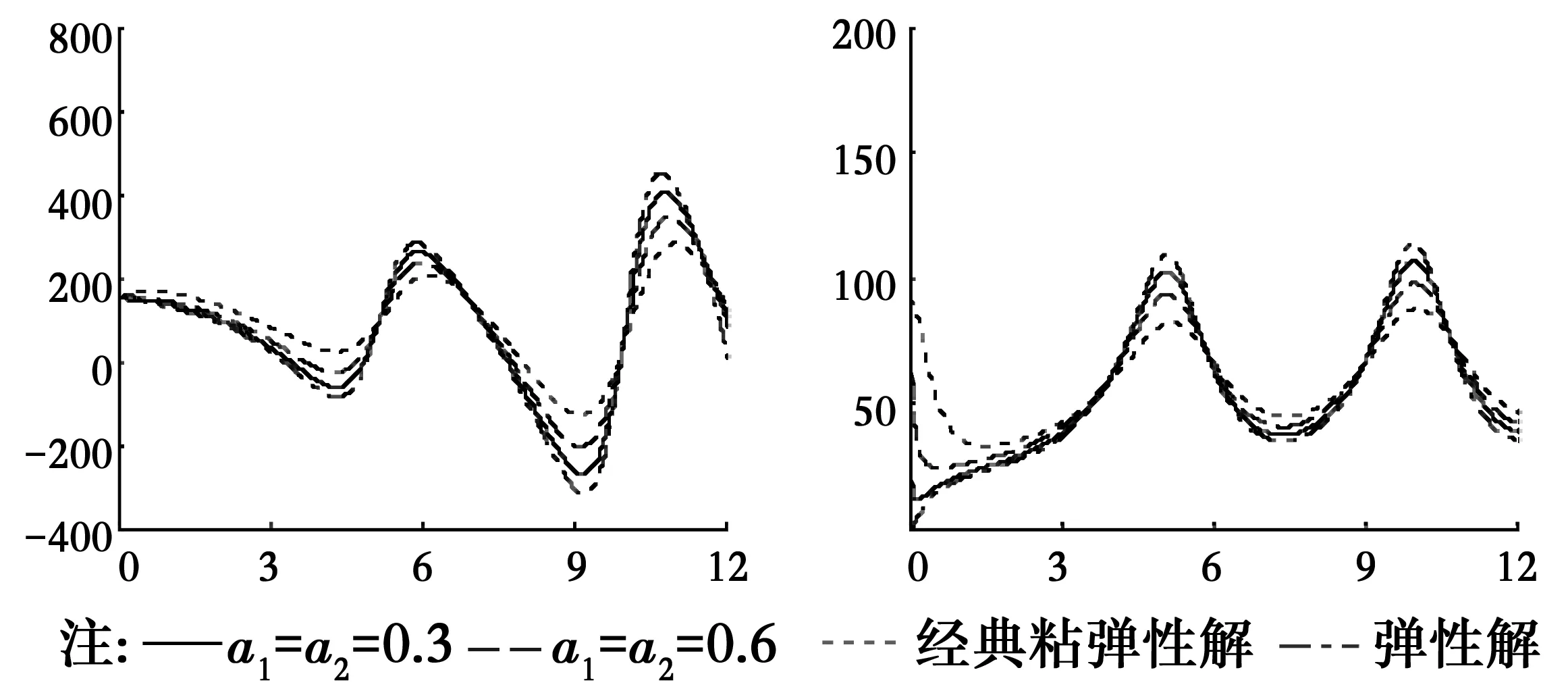
圖2 α13種模型對比分析Fig.2 Contrastive analysis of three models

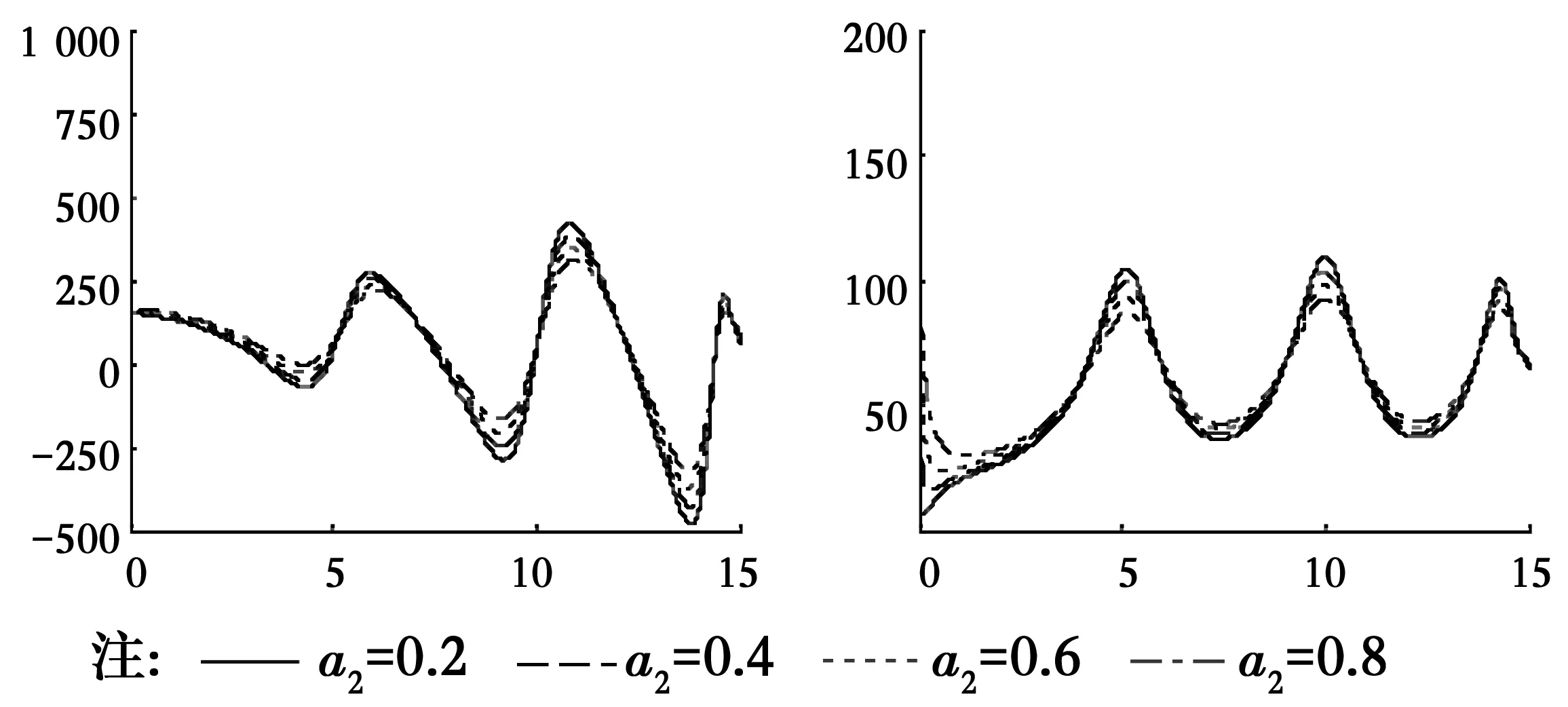
圖3 α1不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.3 Curves of the torsional complex stiffness varying with frequency for different α1

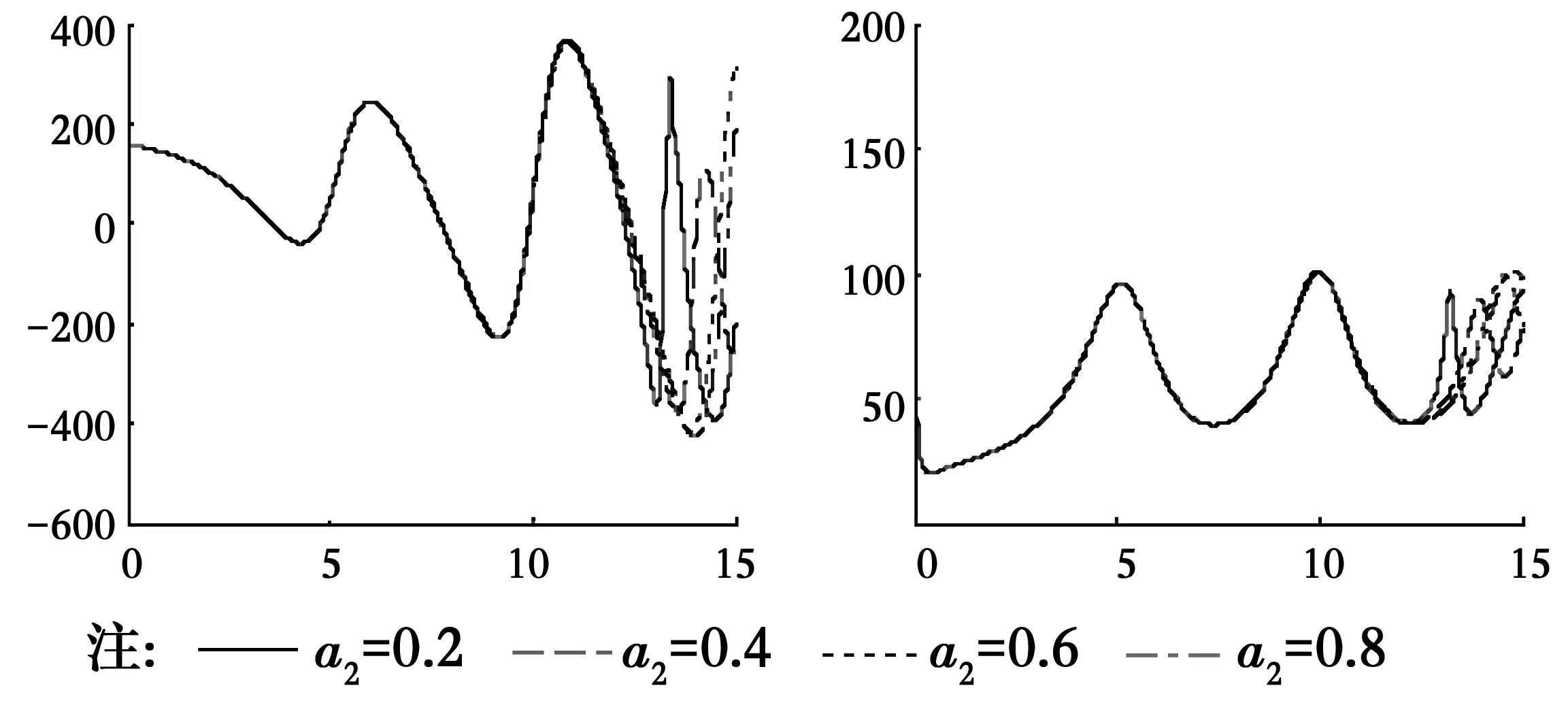
圖4 α2不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.4 Curves of the torsional complex stiffness varying with frequency for different α2

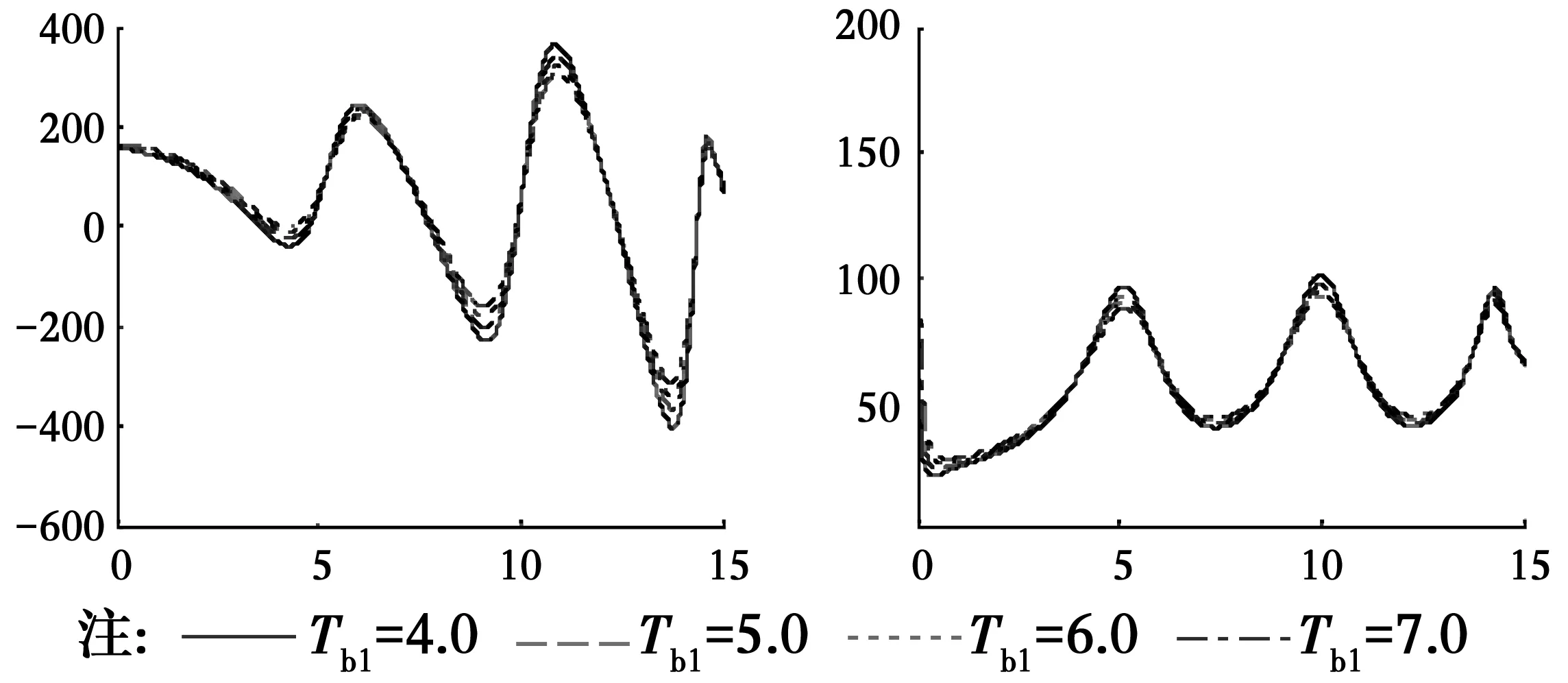
圖5 Tb1不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.5 Curves of the torsional complex stiffness varying with frequency for different Tb1

圖6 Tb2不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.6 Curves of the torsional complex stiffness varying with frequency for different Tb2

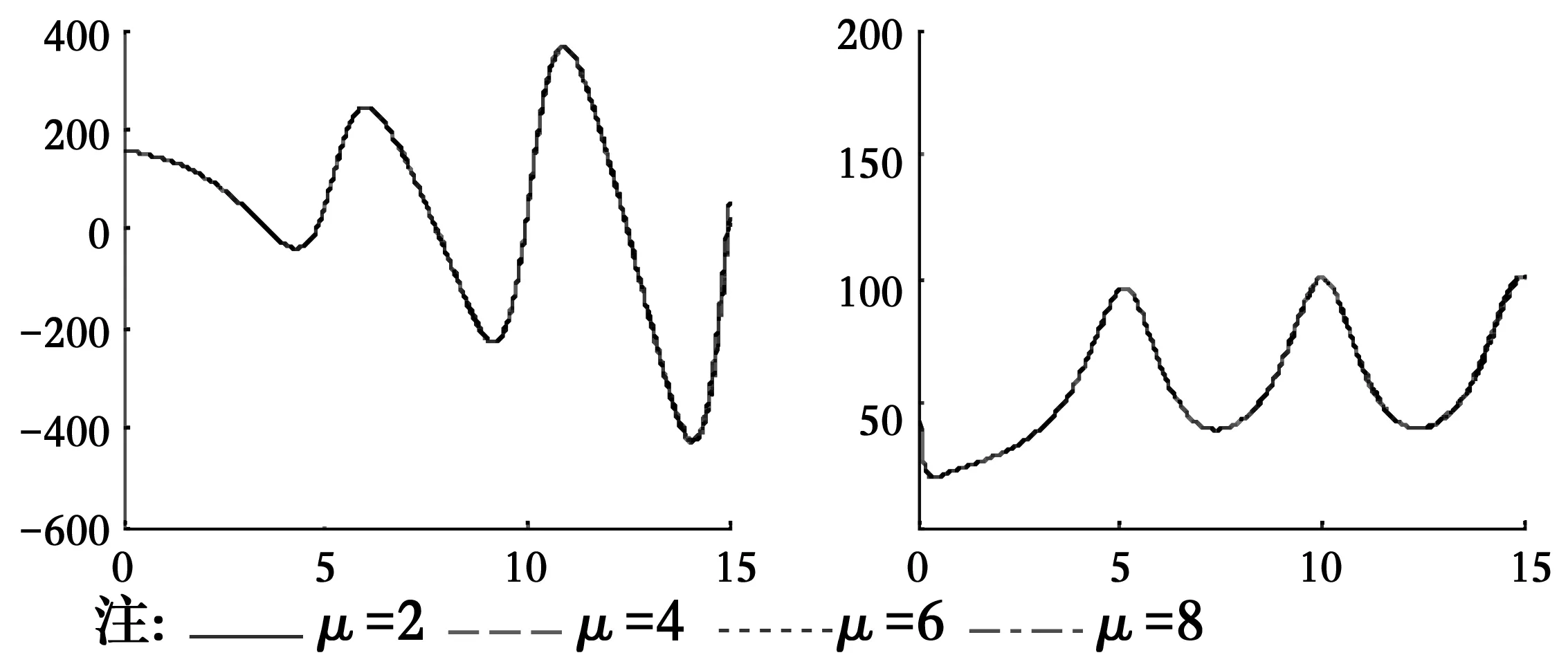
圖7 μ不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.7 Curves of the torsional complex stiffness varying with frequency for different μ

圖8 μ不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.8 Curves of the torsional complex stiffness varying with frequency for different μ

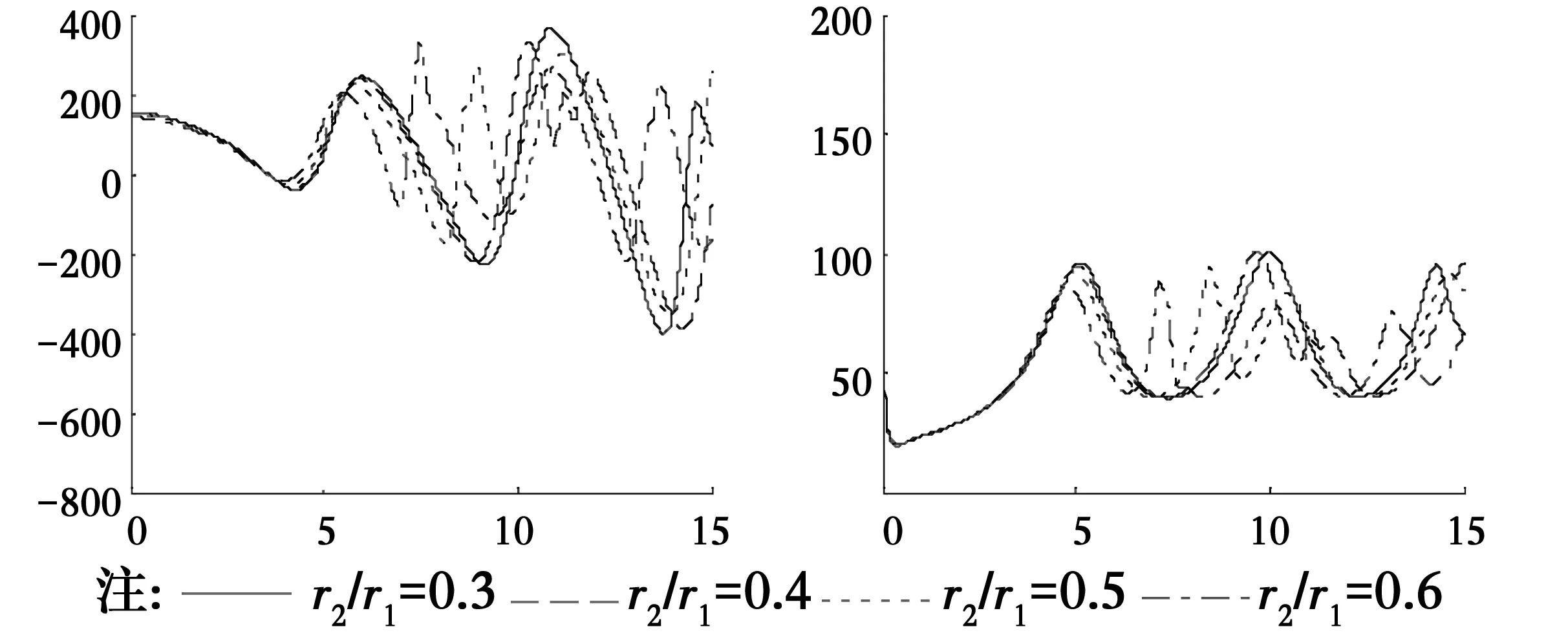
圖9 r2/r1不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.9 Curves of the torsional complex stiffness varying with frequency for different

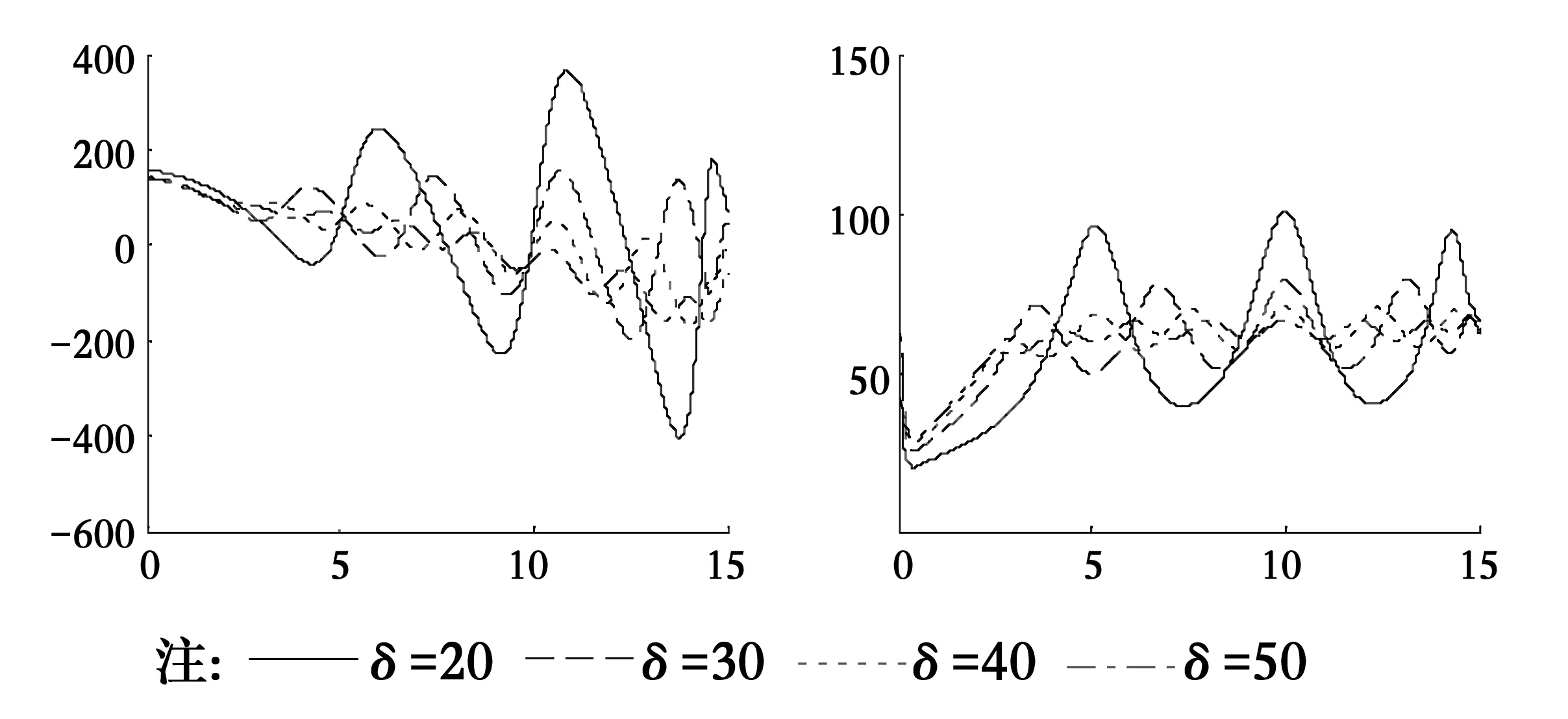
圖10 δ不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.10 Curves of the torsional complex stiffness varying with frequency for different δ

圖11 Gp不同時樁頂扭轉(zhuǎn)復(fù)剛度隨頻率變化曲線Fig.11 Curves of the torsional complex stiffness varying with frequency for different

5 結(jié)論

考慮樁周土和樁芯土的粘彈性特性，并借助分數(shù)導(dǎo)數(shù)Kelvin粘彈性模型描述土體的應(yīng)力-應(yīng)變關(guān)系，研究了分數(shù)導(dǎo)數(shù)粘彈性土中管樁的扭轉(zhuǎn)振動。得到以下主要結(jié)論：

1)樁周土本構(gòu)模型參數(shù)α1和Tb1對管樁的振動的影較大，而樁芯土本構(gòu)模型參數(shù)Tb2和和α2對管樁的扭轉(zhuǎn)振動的影響與頻率有關(guān)，即高頻時有影響低頻時幾乎沒有影響。

2)樁芯土與樁周土剪切模量比μ大于1和小于1時對管樁樁頂扭轉(zhuǎn)復(fù)剛度的影響規(guī)律不同，當樁芯土剪切模量較小時需要考慮樁周土和樁芯土力學(xué)性質(zhì)的差異的影響。

3)管樁內(nèi)外半徑比和長徑比等幾何特性和樁土模量比等力學(xué)特性對管樁扭轉(zhuǎn)振動影響較大，需要重點考慮。