基于模糊數學理論的預制梁場規劃建設及施工管理

梁允偉

(廣西路建工程集團有限公司，廣西 南寧 530001)

0 引言

隨著我國經濟的高速發展和綜合國力的不斷增強，國家對于基礎設施的需求也與日俱增，其中，高速公路建設得到了空前的發展。在高速公路建設過程中，橋梁建設是必不可少的環節。在橋梁工程施工過程中，一般都是在預制梁場中制作預制梁，這是因為采用預制梁結構具有施工方便、施工效率高、施工周期短、便于現場管理等特點。同時，在預制梁場內制作的成品梁經過運輸和吊裝安放到設計位置上，其質量與生產進度直接影響整個工程質量與工期進度[1]。因此，在橋梁的施工期，對于預制梁場的選址以及設計都是極其重要的。針對預制梁場的選址與設計內容包括兩個方面：預制梁場的宏觀選址與細觀設計。本文基于模糊數學的相關方法與應用，利用多屬性模糊決策理論對預制梁場場內布置方案進行評價，建立模糊多屬性決策模型進行計算分析，并驗證其是否與項目實際相符合。

1 預制梁場選址的基本原則與影響因素

1.1 預制梁場選址的基本原則

通常，在主體工程的施工過程中，雖然預制梁場是作為附屬工地，但是其選址的好壞影響著整個工程的工期進度以及施工成本。因此，通過對國內外工程實例的預制場選址分析，總結預制梁場選擇位置時須遵守的原則：

(1)預制梁的生產與橋梁主體工程的施工之間不能相互干擾、相互影響。

(2)應在施工區范圍內或者施工區附近選擇合適的場地作為預制梁場。

(3)預制梁的制作受制作材料的影響，為方便施工，應與工程主體材料相互利用。

(4)地形和地質條件滿足預制梁的生產要求并能盡量減少臨時工程量。

1.2 預制梁場選址的影響因素

除了遵守上述幾項原則之外，預制梁場選址根據項目的生產、進度、工期以及成本的不同要求，其位置選擇有很大的區別。因此，在這里總結以下幾個方面的因素影響[2]：

(1)場地因素，是否具有合適作業面積的場地。

(2)運輸因素，對外交通和對內交通條件是否便利。

(3)費用因素，在保證預制梁的生產效率和質量的前提下，工程成本控制是施工單位考慮的主要目標。

綜上所述，一般情況下預制梁場選址思路如圖1所示。

2 三角模糊決策模型

目前模糊數學的相關方法在工程施工中已經廣泛應用，不斷參照具體適用工程，其研究已經取得巨大的成功[3]。我們可以利用多屬性模糊決策理論對預制梁場場內布置方案進行評價，建立模糊多屬性決策模型進行計算，并驗證其結果是否與項目實際相符合。

2.1 建立評價指標體系

根據預制梁場布置的依據以及影響因素分析，設計方案評價體系見圖2。

(1)生產安全性：指預制梁場的場內布置設計是否能夠保證施工人員安全。

(2)基本生活條件：勞動者在整個工程順利進行中屬于不可缺少的部分。

(3)生產便利程度：根據預制梁生產工序的要求，安排合理的空間布局，在生產預制梁時各種資源的使用有比較好的流水作業線路，避免回流作業，增加成本。

(4)對外交通：若對外交通方便快捷，顯然能夠增加生產效率，有利于成本控制。

(5)內部交通：預制梁生產是一個連續的過程，各個相關功能區的運輸需方便快捷，并且盡可能減少運輸距離，提高工作效率，節約成本。

(6)梁體運輸：在預制梁場設計布置時，必須將梁體運輸的運輸工具、道路情況充分考慮以滿足生產施工需求。

(7)機械化程度：為了提高預制梁場的生產效率，預制梁場在設計的時候應該最大限度發揮機械設備的作用。

(8)土地利用率：預制梁場的布置應該因地制宜，力求以最小的布置用地達到最大的生產力度，滿足項目工程的需要。

(9)梁臺和模具利用率：通過比較精確的定量分析得到合理的生產設計，保證工程能夠按時按質完成目標。

(10)租地與征地費用：通常是采用租賃的形式來獲得場地使用權，要合理地進行租地與征地，在不影響工程進度的情況下，盡可能地節約成本。

(11)場地平整費用：不同的地段，因其地質情況不同可能平整地面的費用也不相同，因此，在合理滿足工程需要的情況下，須盡量減少土地的平整費用。

(12)設備運行和勞動力成本：合理地對機械設備和人工勞動力需求進行分析，得到最適合的配比，達到比較好的成本控制目標。[4]

圖2 評價指標體系示意圖

2.2 構造模糊決策模型

模糊多屬性決策模型相對于傳統的經典多屬性決策模型來說，多了一個模糊因子，使最后的決策更加合理。下面對該模型進行定義：令被評價的方案的集合為C={C1，C2，…，Cm}，每一個方案都有一個自己的屬性，故令屬性集為D={D1，D2，…，Dn}，與此同時，每一個屬性的重要程度不一樣，因此令其相對重要程度權重的集合為ω={ω1，ω2，…，ωn}，但是，在實際的應用中，指標屬性和其權重一般都是語言描述的，有的描述很準確，有的就比較模糊，例如：“不行”表示確定不好，“可能”則表示很模糊，因此，必須利用模糊子集或模糊數來度量這些指標屬性和權重，將具有不確定性的屬性指標、權值和語言描述等都定義成相應的模糊子集或模糊數。其模糊指標矩陣可以定義為R：

(1)

于是模糊決策矢量可表示為：

W=ω⊙R={w1，w2，…，wn}⊙

(2)

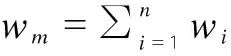
2.2.1 建立綜合三角模糊數互判矩陣

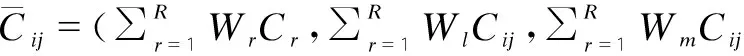
(3)

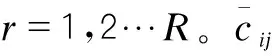
2.2.2 計算評價指標的三角模糊數權重

(4)

2.2.3 建立綜合三角模糊數屬性評價矩陣

一般情況下，我們將傳統的評價語言轉化為具體的數字來表示。但是，數字一旦定下就是一個固定不變的精確值了。然而，對于評價來說，過度的精確評價顯然是不現實的，也不客觀。因此，為了追求更高的準確性和客觀事實性，本文利用三角模糊數來對語言變量進行描述。為了讓計算更加簡便，建立權重相同的三角模糊數等級，此處與語言描述相對應的三角模糊數等級見表1。

表1 語言描述和三角模糊數的轉換關系表

每位專家根據三角評估指標，結合表1中的模糊語言變量數量，建立綜合三角模糊數評估方案得分矩陣，然后通過綜合模糊評估方法的疊加獲得專家權重，綜合三角模糊數評估方案得分矩陣如表2所示。

表2 綜合三角模糊數評估方案得分矩陣表

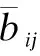
2.2.4 計算三角模糊數總評結果

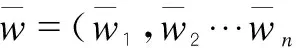
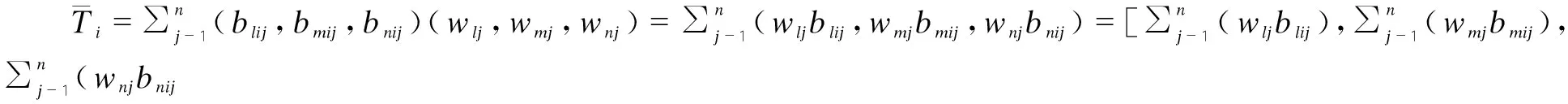
(5)

2.2.5 對被評價方案總評結果的三角模糊數進行排序決策

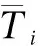
(6)

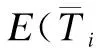
3 應用實例

廣西某高速項目標段，沿線地質條件復雜，是該項目最為突出的一個特點。途經喀斯特巖溶地貌區，山嶺重丘區，地面起伏大，山體陡峭、溝壑沖槽分布廣泛。為了滿足高等級公路所需的技術標準，克服各種不利地形，該高速公路主線的橋梁隧道總長超過70 km，橋隧比高達34.3%，這一比重僅次于河池至百色高速公路。

對常見的預制場以及廣西某高速項目標段預制梁場的布置設計進行評價，分析得到三個預制梁場的布置方案中最符合工程實際需求的布置方案，并對其最后的結果評價，輔助決策者做出正確的選擇。在評價之前，應該找到具有一定權威的專家組成專業評分小組：三位專家的評分結果組建三角模糊互補評價指標矩陣，另有五名專家建立屬性評分矩陣。[5]方案分析如下：

3.1 建立綜合三角模糊數互判斷矩陣

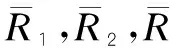
3.2 計算評價指標三角模糊權重

根據公式(3)、(4)，利用MATLAB編程進行數據計算，最終得到關于評價指標的三角模糊數權重值，見表5。

3.3 建立綜合三角模糊屬性評分矩陣

專家打分后，對評分結果進行匯總分析，假設每位專家都具有相同的權威性，方便計算，取等權重wr=1/3，計算結果如下頁表6所示。

表6 綜合三角模糊數評價矩陣表

3.4 計算三角模糊數總評分值

根據公式(5)，對專家判斷信息進行匯總分析得到評價對象的最終三角模糊總評分值如表7所示。

表7 三角模糊總評分表

3.5 計算評價對象的三角模糊數總分值的期望值排序

根據公式(6)，計算評價對象的三角模糊數期望如表8所示。

表8 三角模糊總評分的期望值表

最后，決策者可以根據表8中的評價對象的總體評估水平的預期值和項目實際情況做出全面的決策。如果僅考慮本文所列指標，應選出具有最高預期值的方案，符合項目實際情況。

4 結語

本文在總結施工經驗的基礎上，系統分析了基于模糊數學理論的道路橋梁工程預制梁場的選址與設計。主要研究結果如下：

(1)對比分析了各類型預制梁場特點，總結預制梁場選址的原則與影響因素。

(2)分析預制梁場場內細觀布置的影響因素，從工作環境、交通條件、資源利用、生產成本等四個方面建立預制梁場場內細觀布置方案的評價指標體系，考慮細觀布置方案屬性指標的隨機性與模糊性，運用三角模糊數方法，構建預制梁場場內細觀布置方案優選模型。

(3)以廣西某高速公路中第二標段項目為實例，利用上述模型進行預制梁場的宏觀選址和細觀場內布置方案優選，并與項目實際布置情況進行對比分析，驗證了本文理論模型的可行性與合理性。