基于彈性半空間體理論的路基工作區深度研究
李長鋒
(廣西壯族自治區林業勘測設計院,廣西 南寧 530011)
0 引言
路基承受著自重荷載和從路面傳遞下來的車輛荷載的綜合作用,并在一定深度范圍內處于受壓狀態。路基土作為一種顆粒性材料,自身的空隙特征使其在受壓的情況下極易產生變形,而這種變形如果無法得到有效控制,將使路面由于失去路基均勻的支撐而產生各類病害,如斷裂、板底脫空、車轍以及沉陷等。合理的結構設計,應對路基在正常使用狀況下的受力狀態、變化規律和力學響應進行分析,使豎向變形處于可恢復的彈性范圍,以保障路基結構的強度和穩定性以及與路面的協調變形[1]。路基工作區作為現行設計規范中表征路基主要承受車輛荷載范圍的控制指標,通過對不同區域填料和壓實度的要求,很好地指導了工程實踐,但目前仍然存在著概念不清晰和缺乏具體的工作區深度計算方法的問題,以致于在路基設計時盲目套用規范給定的壓實、淺層換填或地基處理范圍,造成了資源浪費,不利于工程人員進一步挖掘規范的內涵及深入理解路基結構在荷載作用下的應力應變特性。
本文以彈性半空間體上作用集中荷載來模擬路基的受力狀態,并通過Boussinesq法計算推導出典型路面結構下路基工作區的深度,為工程應用提供理論依據。
1 Boussinesq法求解荷載豎向附加應力
為了模擬車輛荷載作用對路基所產生的附加應力狀態,并求出該荷載所產生的豎向應力σZ,現將路基土假定為在水平方向和向下深度上都是無限延伸的各向同性的均質線彈性變形體。同時,可認為路基中某應力計算點位與車輪印跡所產生的均布荷載的距離遠大于均布荷載本身的面積,這樣就可將車輪荷載用一個集中力來代替,應用Boussinesq法求解半空間體路基內部任何一點的應力和位移。
這是一個空間軸對稱問題,車輪荷載簡化成的集中力P的作用線即為對稱軸,半空間內任意一點M的坐標為(x,y,z),對M點的正六面體單元體進行應力狀態分析可得到6個應力分量和3個位移分量,R為M點至原點的距離,如圖1所示。
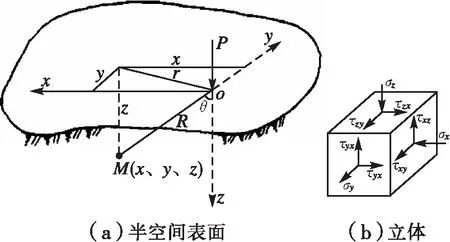
圖1 集中力作用下彈性半空間內任意點的應力狀態示意圖
利用彈性力學對單元體進行分析,解得:
(1)
σz:τzy:τzx=z∶y∶x
(2)

(3)


2 當量土層厚度換算及自重應力計算
由于路基在實際工作中只是作為路面結構的支撐,車輪荷載并不直接作用在路基上,路基只承受著荷載的擴散作用。考慮到路基路面之間的材料特性和彈性模量相差較大,因此,為了滿足彈性半空間體均質和各向同性的假設,必須進行當量換算[2]。
根據彈性力學中相同荷載作用下,路面結構變形或應力與各層次的回彈模量、泊松比以及厚度密切相關的性質,可將某一已知彈性參數和層厚的結構層按照彎沉不變的原則,等效換算成另一種模量和層厚,這種彈性原理也是應用半空間體進行有鋪面情況下路基土內荷載附加應力計算模型的基礎,如圖2所示。

圖2 路面結構等效換算示意圖
以瀝青路面為例,按照彎沉等效的原則,換算公式如下:
(4)
公式中:hi——瀝青路面各結構層厚度,以cm計;
鴨瘟俗稱大頭瘟,是由鴨瘟病毒(DPV)感染鴨、鵝和其他雁形目禽類引起的一種急性、熱性、敗血性傳染病。臨床特征主要表現為高熱、兩腳無力、下痢、口渴、流淚,部分病鴨頭頸部腫脹。大腸桿菌病是一種能以多種病病型表現的疾病,其發病與環境因素密切關系,在臨床上多以原發或繼發于其它疾病而出現。
Ei和E0——各結構層及路基土對應的回彈模量值,以MPa計。
由(4)可知,路面結構層材料的回彈模量越大,換算成當量土層厚度就越厚,可解釋為路面層的應力擴散效應越明顯。
根據現行規范定義,是以路基內某一深度處荷載產生的豎向附加應力與土體自重應力的比值為0.1~0.2時,該深度區間即為路基工作區,該區域路基土體受車輪荷載影響較大,需采取更好的填料或更高的壓實標準。所以,若在計算時不考慮路基土與路面材料的重度差異,路基工作區Za可按下式推導得出:
(5)
(6)
公式中:γ——路基土重度,以kN/m3計;
n——0.1~0.2。
若需要考慮路面各結構層自身重度的差異,則可用試算法求得Za。
3 軸載參數分析
為了求解方便,將標準軸一側的車輪荷載采用單圓圖示進行換算[3],如圖3所示。
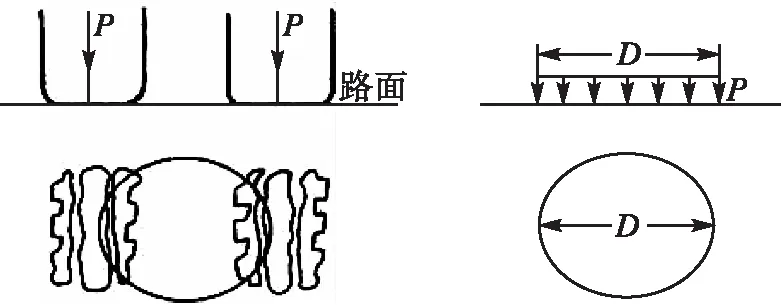
圖3 單圓荷載計算示意圖
根據路面設計,標準車黃河JN150,路面承受的標準荷載為100 kN,由于標準軸一側輪載為50 kN,并且取輪胎接觸壓力為0.70 MPa。經過單圓圖示的計算公式,求得荷載的半徑為15 cm,由于確定路基工作區范圍的應力計算點與均布荷載的距離遠大于均布荷載本身,所以可進一步簡化為作用于彈性半空間體上的垂直荷載,這樣就建立了Boussinesq的荷載模型。
4 工程應用
在工程實踐過程中,經常會遇到各種地基不良現象或低路堤情況,前者通常為承載力不足的軟土地區,若車輛荷載傳遞到軟土層的應力過大,則極易產生變形沉陷;而在平原地區修筑公路,受標高的限制,低路堤是普遍存在的路基形式,為了保證路基的強度和穩定性,必須對原地面一定深度的土層進行特殊處理[4][5][6]。
現以某省一級公路路基淺層換填為例,通過定量計算路基工作區來明確換填深度。
4.1 工程概況
該設計路基段為低填方路基,平均高度h=0.8 m,土質為粉質黏土,重度為18 kN/m3,荷載等級為重交通,路基頂面回彈模量E0=70 MPa。路面結構層從上至下依次為4 cm厚細粒式瀝青混凝土AC-13、6 cm厚中粒式瀝青混凝土AC-20、8 cm厚粗粒式瀝青混凝土AC-25、30 cm厚水泥穩定基層、20 cm厚級配碎石底基層、路面總厚度h1=68 cm。
經查閱可知交通荷載參數,路基路面結構層物理力學參數如表1~2所示。

表1 交通荷載參數表

表2 路基路面結構層物理力學參數表
4.2 換填深度計算
路面結構層當量換算厚度:
路面結構底層以下工作區深度:
H=Za-Ze=2.981-2.237=0.744 m
該計算結果與重交通一級公路路床范圍(0~80 cm)基本相符,說明基于彈性半空間理論的路基工作區深度計算方法可信。
則路基換填深度:
hc=H+h1-h=0.744+0.68-0.80=0.624 m
5 結語
本文詳細推導和總結了基于彈性半空間理論的車輪荷載豎向附加應力的取值換算原則,明確了路基工作區深度的計算過程,并進行多種軸載試算以研究超載對路基的影響,為實際工程應用中關于淺層換填、地基處理深度提供了理論依據和計算實例。進一步研究建議如下:
(1)垂直荷載作用于彈性半空間體模型對于分析有路面結構的路基應力經過換算和假設,與實際情況相差較大,特別是路面結構對荷載的擴散效應未進行充分考慮,可利用計算機程序深入研究彈性層狀體系模型下的應力響應。
(2)現規范對汽車荷載的簡化仍然基于靜態垂直荷載,為了更準確地反映汽車的實際作用狀態,應對動載進行深入研究,分析路基結構在動載作用下的附加應力。
(3)對路面結構進行當量土層厚度換算時采用彎沉等效的原則,而路基工作區的計算卻以應力之比作為控制指標,存在設計方法與評價指標不一致的缺陷,可深入研究采用荷載附加應力等效的方法重新換算土層厚。
(4)引入路基工作區概念的本質是限制路基在車輪荷載高應力區的塑性變形,以免路面失去有效均勻的支撐而產生破壞,但工作區的計算卻忽視了對變形這個核心參數的限制,可繼續研究基于控制應變的計算方法。
(5)工程應用中,用理論計算的方法確定了淺層換填或地基處理的深度,但未考慮換填填料的物理力學性質或處理措施不同而帶來的差異,可根據工程中常用的填料類型進行分組試驗,并通過回歸分析引入材料參數,進一步修正理論公式。

