機載衛星雙星天線饋源運動學分析與ADAMA仿真

吳碩才 ，徐 雷 ，任清川 ，何思奇

（1.四川大學 制造科學與工程學院，成都 610000；2四川九洲電器集團有限公司，綿陽 621000）

由于目前大多數衛星天線都只能跟蹤一顆衛星，利用龍伯透鏡多焦點的特性，設計雙星跟蹤天線成為未來衛星發展的方向。對雙星系統饋源進行運動學分析，解算出雙星天線俯仰軸與方位軸與空間坐標系之間的轉換關系，能夠為雙星系統運動避障問題奠定基礎。文獻[1]直接運用幾何關系，對機器人雙臂末端的坐標進行運動學分析，最終實現了雙臂機器人的實時避障。文獻[2]通過向量相加，對三自由度搖擺臺實現不同坐標系之間的相互轉化，從而對其進行運動學分析，并且運用Matlab與ADAMS進行仿真，結果表明Matlab數值計算與ADAMS仿真結果一致，證明了運動學分析的正確性。文獻[3-7]采用標準的DH法對機器臂進行運動學建模，然后利用反變換法結合幾何法將機械臂的姿態用角度表示。文獻[8]運用閉環理論對一種新型結構的機器人進行運動學分析，使得運動學等式的建立更加簡單。DH建模法適用于關節個數較多的機構進行運動學分析，由于機載衛星通信雙星天線的關節個數較少，直接采用幾何法建立正運動學模型，能夠簡化運動學模型，使得求解逆運動學表達式更加簡便，從而提高計算效率。通過Matlab對所得表達式進行數值計算，將所得結果與AMAMS仿真結果對比，驗證求解表達式的正確性，為雙星天線運動規劃和避障奠定基礎。

1 雙星系統虛擬樣機的建立

1.1 建立三維實體模型

該衛星雙星系統主要由2個重疊的俯仰軸和方位軸、4對電機和減速器、支撐座以及龍伯透鏡組成，其中4對電機和減速器分別驅動2個重疊的俯仰軸和方位軸旋轉，使得2個饋源能掃描完龍伯透鏡的整個半球面，由于2個饋源底面距離透鏡中心的距離相等，因此在運動的過程中就有可能發生碰撞。運用三維建模軟件UG建立了機載衛星通信雙星天線實體模型，其三維模型如圖1所示，各關節的運動范圍為 0°～180°。

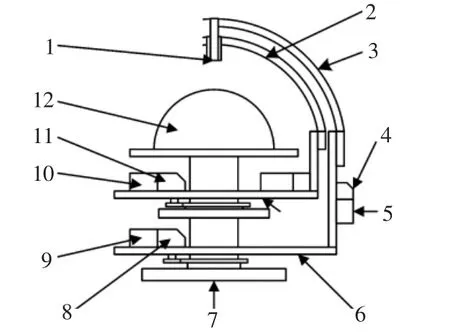
圖1 機載衛星通信雙星天線實體模型Fig.1 Airborne satellite communication binary star antenna solid model

其機構運動簡圖如圖2所示。

圖2 雙星天線機構運動簡圖Fig.2 Schematic diagram of the motion of a two-star antenna mechanism

1.2 建立雙星系統的數學模型

由于俯仰軸與方位軸具有重疊效應，因此只選用其中一個方位軸與對應的俯仰軸進行運動學分析。由幾何關系可知俯仰軸和方位軸的旋轉運動可以轉化為饋源在球面上的復合運動，其簡化數學模型如圖3所示。當俯仰軸轉動一定角度等價于饋源在豎直平面內轉過相同的角度，而方位軸轉動一定角度等價于饋源在水平面內轉過相同的角度。

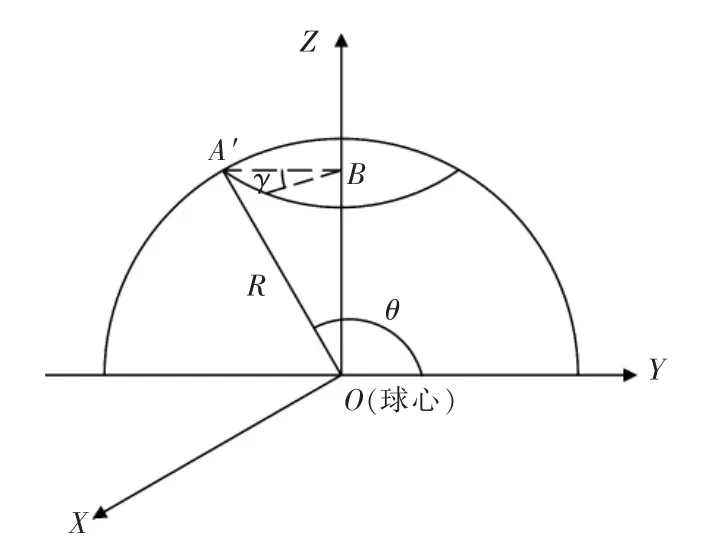
圖3 數學簡化模型Fig.3 Mathematical simplification model

圖3中假設饋源底面中心點到龍伯透鏡球心的距離為R，θ為俯仰軸從零點開始轉過的任意角度，γ為方位軸從零點位置轉過的任意角度，反映了雙星天線運動過程的運動規律。

2 雙星系統運動學分析

對于雙星饋源的運動控制其實質就是對俯仰角、方位角的控制，直接的控制量是俯仰軸和方位軸的運動角度，而同時饋源也處于三維坐標空間當中，因此三維坐標與俯仰角、方位角之間的轉換關系是雙星系統避障策略研究的重點問題。這過程主要包括2個方面的內容，一是給定雙星系統俯仰角和方位角，求雙星系統饋源的位置，稱之為運動學正問題；二是給定雙星系統饋源的位置，來求雙星饋源的俯仰角和方位角。

2.1 運動學正向解

將雙星天線的運動分解為俯仰運動和方位運動，假定俯仰軸轉過θ角度，而方位軸轉過γ角度，饋源離龍伯透鏡球心的距離為R。由幾何關系可得：

因此可以得到當俯仰軸轉過任意θ角、方位軸轉過任意γ角，饋源底面中心點在空間三維坐標系OXYZ 中的坐標為（-Rcosθsinγ，Rcosθcosγ，Rsinθ）

2.2 運動學逆向解

當只知道饋源在空間坐標系中的空間坐標，而不知道各個俯仰角和方位角時，此時就必須要求出運動學的逆向解，即求出各個俯仰軸和方位軸的旋轉角度。 假設某時刻饋源的坐標為（x，y，z），由前式（1）～式（3）可以反解出俯仰角 θ和方位角 γ。

3 數值計算及ADAMS模型軌跡運動仿真

3.1 數值計算

按照上述討論提出的算法，取R=150 mm，以轉過為分界線，分4種情況在Matlab軟件內編寫m函數進行數值計算，得到4種情況下的數值計算軌跡。其 4 種情況分別為①θ≤90°，γ≤90°；②θ≤90°，γ＞90°；③θ＞90°，γ≤90°；④θ＞90°，γ＞90°。

3.2 數值計算及ADAMS仿真結果

ADAMS虛擬樣機仿真能夠直觀地觀察到雙星天線在給定的俯仰角和方位角下饋源的運動軌跡，并能得到饋源在運動過程當中的位移參數變化情況，對上面數值計算進行一定的驗證。

3.2.1 仿真設置

通過對機載衛星通信雙星天線的運動過程分析，對天線的運動結構進行簡化，其簡化模型如圖4所示。

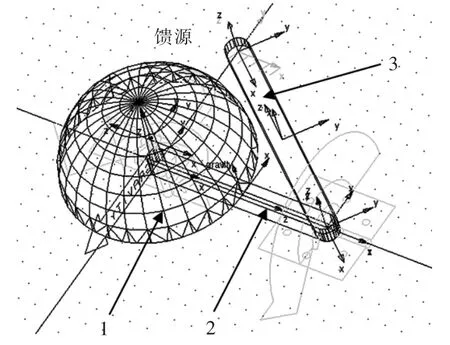
圖4 饋源運動簡化模型Fig.4 Simplified feed source motion model

為了保證與數值計算的參數一致，仿真時同樣選擇 4 組數據進行實驗，即：①θ＝0～60°，γ＝0～60°；②θ＝0～60°，γ＝0～120°；③θ＝0～120°，γ＝0～60°；④θ＝0～120°，γ＝0～120°。在對俯仰軸和方位軸施加驅動時選擇ADAMS中的STEP階躍函數[9]定義旋轉驅動，如第一種情況采用 step（time，0，0d，10，120d）；step（time，10，0d，20，120d）。

接著對仿真控制器進行設置。持續時間選擇20 s，輸出仿真結果的步數設置為500。仿真開始以后，饋源首先以（0，150，0）點為零點，在 Y-Z 平面 0～10 s內繞X軸旋轉，10 s～20 s內改變方向，在X-Y平面繞著Z軸旋轉。

3.2.2 仿真結果

將ADAMS環境中仿真測量的數據導入到Matlab中，將這兩類數據在一張圖中繪出進行比較，其結果如圖5～圖8所示。

從上述4張圖中可以看出，無論俯仰軸與方位軸如何變化，數值計算結果與仿真結果所得曲線均完全重合，由此可見Matlab數值計算結果與ADAMS仿真結果完全一致，從而驗證了推導的運動學正向解的正確性，為雙星天線的運動規劃和避障奠定基礎。

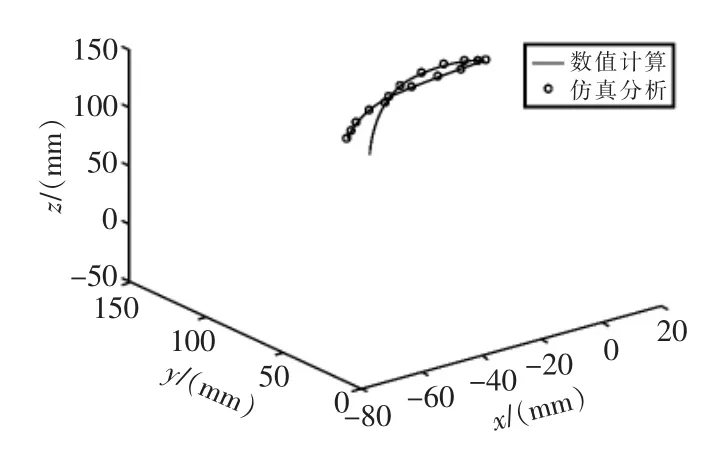
圖5 θ＝0～60°，γ＝0～60°的數據對比圖Fig.5 Data comparison diagram of θ＝0～60°，γ＝0～60°

圖6 θ＝0～60°，γ＝0～120°的數據對比圖Fig.6 Data comparison diagram of θ＝0～60°，γ＝0～120°

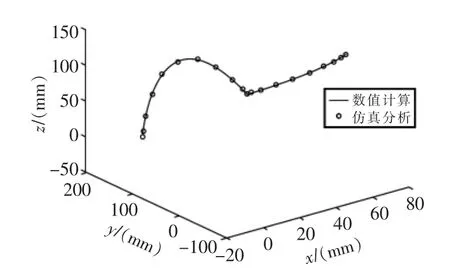
圖7 θ＝0～120°，γ＝0～60°的數據對比圖Fig.7 Data comparison diagram of θ＝0～120°，γ＝0～60°

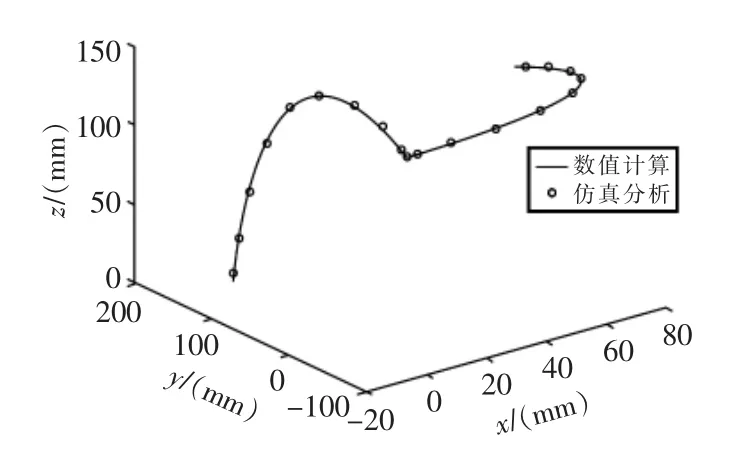
圖8 θ＝0～120°，γ＝0～120°的數據對比圖Fig.8 Data comparison diagram of θ＝0～120°，γ＝0～120°

4 結語

隨著衛星通信在日常生活中越來越重要，雙星天線將有著巨大的發展潛力。對機載衛星雙星天線饋源進行運動學分析，解算出雙星天線俯仰角、方位角與饋源在空間坐標系OXYZ中的位置坐標之間的數學關系，對于解決雙星天線碰撞問題有著重要作用。同時ADAMS擁有強大的運動學和動力學分析功能，運用軟件進行仿真，將所得結果與Matlab數值計算所得結果進行比較，能夠在很大程度上對所得結果進行驗證。