極值分布模型在動車組空調機組可靠性分析中的應用研究*
錢小磊
(北京縱橫機電技術開發公司,北京 100081)
極值分布模型是可靠性建模中常用的一種,模型具有參數少、實用性強的特點。以實際運行動車組空調機組的故障數據為對象,研究了極值分布函數在動車組空調機組可靠性建模中的應用,重點研究了參數估計和分布擬合檢驗的方法及應用,期望為其他動車組產品的可靠性建模提供借鑒和參考。
1 動車組空調機組故障數據處理
可靠性試驗一般的做法是從總體中隨機抽取n個樣品,在規定的工作條件下將其全部試驗至發生故障并記錄其觀測值,得到樣本故障數據。與常規可靠性試驗不同的是,動車組每臺空調機組裝車上線運行的時刻不完全相同,即各個樣品開始試驗的時間起點不完全相同。為研究動車組空調機組的可靠性或故障規律,可引進空調機組發生故障時的運行里程T作為隨機變量,將所有空調樣品的試驗“拉回”里程零點(即從里程t=0起計)統計各個空調的故障里程,如圖1所示。
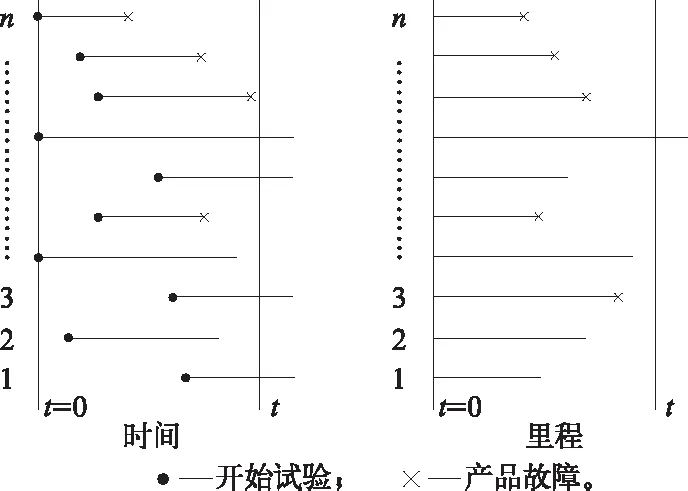
圖1 空調機組可靠性試驗數據
根據現行動車組檢修規程,空調機組五級修(運行480萬km或12 年)時其主要部件如壓縮機、換熱器、風機等需要更新,修復程度接近再制造,因此可將空調機組的可靠性試驗看作試驗終止里程為480萬km的定時截尾試驗。將試驗終止里程均分成k個里程區間 ,統計每個區間的故障(須為首次故障)空調臺數 和該區間內的空調機組總臺數 (與固定樣本容量不同,每個區間的樣本數量為實際已運行至該區間下限里程的空調機組數量,因此各區間的樣本數不完全相同,數據具有變樣本容量的特點),則故障頻率為:
(1)
累積故障頻率為:
(2)
2 極值分布可靠性建模基本原理
2.1 模型介紹
極值分布概率密度函數:
f(t)=λexp[-λ(t-μ)-e-λ(t-μ)]
(3)
分布函數:
F(t)=exp[-e-λ(t-μ)]
(4)
2.2 參數估計
參數估計的常用方法有矩估計、極大似然估計、最小二乘估計等,考慮極值分布函數表達式可經變量變換轉化為線性形式,采用最小二乘估計法。F(t)兩邊取對數有:
ln[-lnF(t)]=-λt+λμ
(5)
令yi=ln[-lnF(ti)],a=λμ,b=-λ,則分布函數變為:
yi=a+bxi
(6)
(7)
(8)
則參數估計值:
(9)
2.3 擬合檢驗
(1)χ2擬合檢驗
設總體X的分布函數為F(x;θ1,…,θl),θ=(θ1,…,θl)是未知參數,檢驗假設:
H0為總體X的分布函數為F(x;θ1,…,θl)
H1為總體X的分布函數不是F(x;θ1,…,θl)

(10)
對于給定的顯著性水平α,拒絕域為:
(11)

(2)線性回歸假設檢驗
極值分布模型經變量變換可轉化為線性回歸模型,因此也可運用回歸分析的假設檢驗方法,文中采用t檢驗法。
設線性回歸模型:
Y=a+bx+ε,ε~N(0,σ2)
(12)
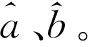
H0:b= 0
H1:b≠ 0
經證明,當H0為真時b=0,此時
(13)

(14)
當假設H0被拒絕時,認為回歸效果是顯著的;反之則認為回歸效果不顯著。
3 實例分析
以某型動車組客室空調機組為例,將該型空調的0~480萬km總運行里程劃分為16個里程區間,統計每30萬km區間內的樣本空調數、首次故障空調數Δri,根據前文公式計算出故障頻率、累積故障頻率等可靠性指標,結果如表1所示。

F(t)=exp[-e-0.014 7(t-133.803)]
(15)


表1 某型客室空調機組可靠性指標計算細表

圖2 某型客室空調機組故障頻率直方圖
因此認為線性回歸的效果是顯著的。該型客室空調機組故障概率分布擬合的效果可見圖3。

圖3 某型客室空調機組故障 概率分布擬合效果
4 結束語
針對動車組空調機組現場故障數據具有變樣本容量、截尾性質的特點,以極值分布模型的應用為例研究了可靠性建模過程。通過對常規可靠性指標計算和假設檢驗方法作適當變化和合理運用,參數估計和分布擬合檢驗均取得理想效果。實際算例表明,極值分布模型可較好反映某型動車組空調機組的可靠性特征,卡方擬合檢驗法可有效用于極值分布函數的假設檢驗。

