分數階控制器在光電吊艙控制中的應用

長春理工大學 電子信息工程學院，吉林長春 130022

一、引言

20世紀80年代，基于各種復雜系統研究基礎之上，分數階微積分在控制領域的應用受到研究者關注[1]。目前工業控制系統中大多采用傳統的PID控制器，分數階PIλDμ是傳統PID的一般性，因其多了兩個參數λ、μ，其過程更細膩、更具有靈活性，分數階PIλDμ控制器比整數階PID控制器有更好的控制品質、動態特性和更強的魯棒性[2]。

在實際控制系統中，常常會伴有強干擾和噪聲的影響，1960年卡爾曼（Kalman）提出了卡爾曼濾波理論，把狀態空間概念引入估計理論中，采用時域上的遞推算法在數字計算機上進行數據濾波處理，卡爾曼濾波在控制領域得到廣泛應用[3]。

本文首先運用MatLab軟件中可視化系統辨識工具箱模塊對光電吊艙俯仰環進行數學模型參數辨識，在不考慮擾動條件下對系統模型設計分數階控制器進行仿真分析，通過改變系統增益大小分析對比得出，采用分數階控制器控制，系統具有較強的增益魯棒性。實際控制系統中常伴有擾動和噪聲，單純的分數階控制器無法抑制擾動的影響，在分數階控制器基礎上加入卡爾曼濾波器對噪聲進行濾除，仿真結果顯示，卡爾曼濾波器與分數階控制器結合對吊艙系統控制，可以有效濾除噪聲，增強系統魯棒性和抗干擾能力。因此，對分數階控制器和卡爾曼濾波器的理論與應用研究有重要意義。

二、分數階微積分及分數階控制器

1、分數階微積分理論

分數階微積分主要研究任意階次的微分、積分算子的特性及其應用。其一般分數階表達式為：

t1—微積分的上限；

t0—微積分的下限；

α—實數或復數；

Re(α)—復數α的實部。

對于分數階微積分的定義，不同的數學家給出不同定義，在實際控制系統應用中，Caputo分數階微積分定義更適合分數階微積分初始值問題的求解[4]。

2、分數階控制器

分數階控制系統采用分數階微分方程描述，對于單輸入單輸出的分數階系統模型，可描述為：

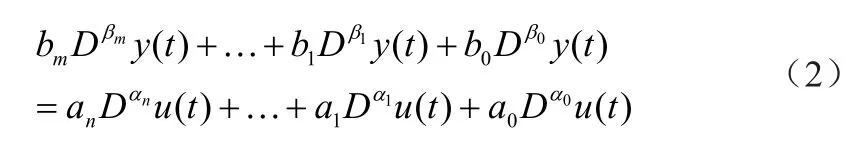
其中，αi(i=1, 2,…,n)、βj(j=1, 2,…,m) —任意實數；

滿足αn>αn-1>…>α0>0，βm>βm-1>…>β0>0，對上式進行拉普拉斯變換，可得到分數階控制系統的傳遞函數為：

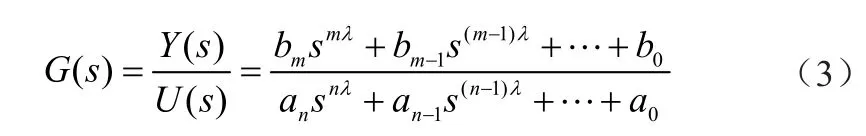
不同的控制系統和不同的控制器，可以將其分為以下幾類：

（1）整數階控制器控制的整數階控制系統；

（2）整數階控制器控制的分數階系統；

（3）分數階控制器控制的整數階系統；

（4）分數階控制器控制的分數階系統[5]。

對于分數階控制器，微分方程式為：

其中，Kp—比例系數；

Kd—微分系數；

Ki—積分系數；

μ—微分階數；

λ—積分階數。

經拉式變換得到對應時域傳遞函數表達式：

控制器對應的結構框圖如圖1所示。

三、卡爾曼濾波器和分數階控制器實現

1、分數階控制器實現

分數階PIλDμ控制器設計是根據系統性能指標，得到滿足系統要求的分數階PIλDμ控制器優化Kp、Ki、Kd、λ、μ參數的過程。控制器參數的選擇對控制系統起關鍵性作用，采用幅值裕量和相位裕度法對分數階PIλDμ控制器進行參數整定。對于給定的相位裕度φm和截止頻率ωc，根據參數整定規則，利用MatLab優化工具箱中fmincon非線性優化函數方法，可以求得分數階 PIλDμ控制器Kp、Ki、Kd、λ、μ參數值[6]。控制器表達式為：

利用AL-Alaoui+CFE脈沖響應不變法對分數階控制器進行離散化數字實現[7]。

2、卡爾曼濾波器實現

卡爾曼濾波理論以最小均方誤差為估計的最佳準則，對于狀態空間模型為：

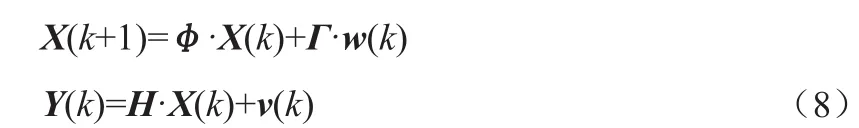
其中，A—狀態矩陣；

B—輸入矩陣；C—輸出矩陣；

D—前饋矩陣，一般為零。離散化后狀態空間模型為：

Γ—噪聲驅動；

H—觀測噪聲；

k—離散時間；

X(k) —表示系統在k時刻的狀態；

Y(k) —對應狀態的觀測信號；

w(k) —白噪聲；

v(k) —觀測噪聲。

卡爾曼濾波的遞推算法流程圖如圖2所示[8]。在一個濾波周期內，由預測狀態變量可知，根據k時刻的狀態估計預測k+1時刻狀態，預測誤差協方差是對預測的質量優劣做定量描述，該預測描述了卡爾曼濾波時間更新過程，測量更新中各式是用來計算對時間更新值的修正量，該值由等信息所確定，最終結果可以合理利用觀測信號Y(k)。只要給定初值和P0，根據k時刻的量測Zk，就可以計算得到k時刻的狀態估計

四、算法仿真分析

1、光電吊艙俯仰環模型建立

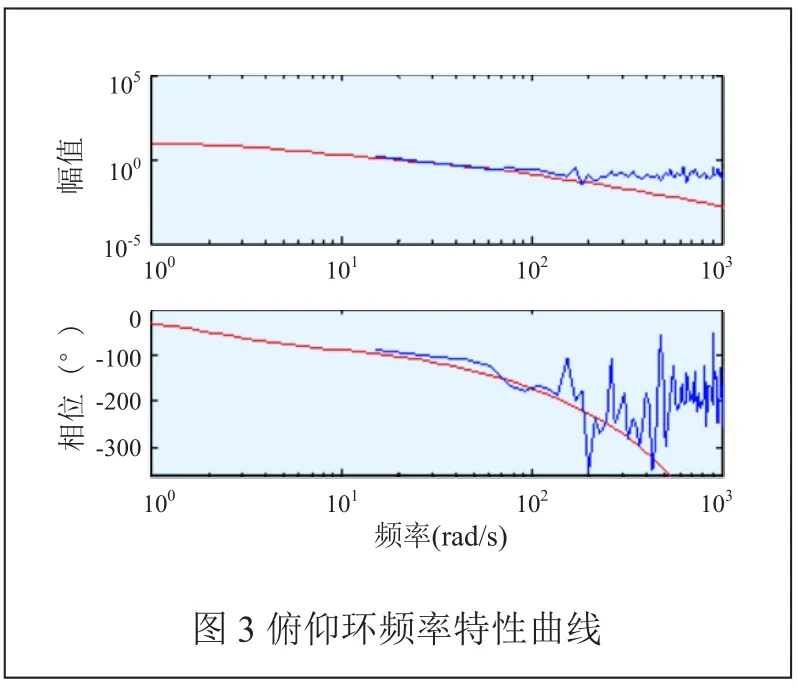
光電吊艙是包含線性和非線性因素的負載系統，難以通過物理建模法得到準確的系統模型，因此采用系統辨識的方法建立數學模型，通過實測輸入輸出數據對模型進行參數辨識。將某光電吊艙航向掃頻信號作為系統輸入，求得吊艙俯仰環在不同頻率段的響應特性，最后通過系統辨識法求取系統的頻率特性[9]。

通過可視化系統辨識工具箱對系統進行參數辨識[10]，最后取部分實驗數據對辨識模型進行驗證，擬合得到俯仰環頻率特性曲線如圖3所示，不考慮延遲環節，近似得俯仰環的傳遞函數如下：

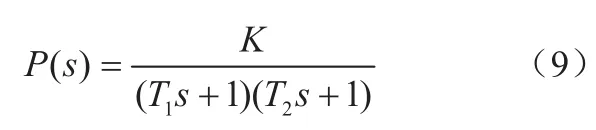
其中，K=1.449、T1=0.11、T2=0.0091。

2、仿真分析

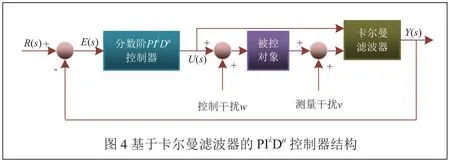
基于卡爾曼濾波器的分數階PIλDμ控制器結構框圖如圖4所示。其中，被控對象采用零階保持器進行離散化，分數階控制器根據前文研究方法進行離散化實現，在系統運行和測量過程中產生的擾動經過濾波器濾除后的值Y(s)反饋到輸入端與預定值進行比較后得E(s)，作為控制器的輸入值，U(s)為控制器的輸出，w為控制干擾（過程噪聲），v為測量噪聲。

采用分數階控制器與卡爾曼濾波器結合控制，假設系統開環截止頻率ωc=90rad/s，相位裕度φm=60°，采樣時間ts=0.001s，系統過程噪聲和測量噪聲均為協方差1，幅值0.02的白噪聲，即Q=1，R=1，初始值P0=B*Q*B′。

由已知條件，根據參數整定規則，得分數階控制器各參數為Kp=7.7212、Ki=35.6517、Kd=1.5847、λ=0.7404、μ=0.2558，傳遞函數表達式為：

加入噪聲前改變系統增益大小，Kp分別取原值的0.8倍、1.0倍、1.2倍，輸入階躍信號，仿真結果如圖5所示。根據仿真結果可以得出系統動態響應特性，如表1所示。

根據結果分析可以得出，改變系統增益大小，系統動態響應特性變化較小，證明系統具有較強的增益魯棒性，參數攝動不敏感，系統對控制輸入信號具有良好的跟蹤能力[11]。

加入濾波后，系統狀態描述如下

將連續時不變系統轉換線性離散時不變系統：初始誤差協方差P0為：

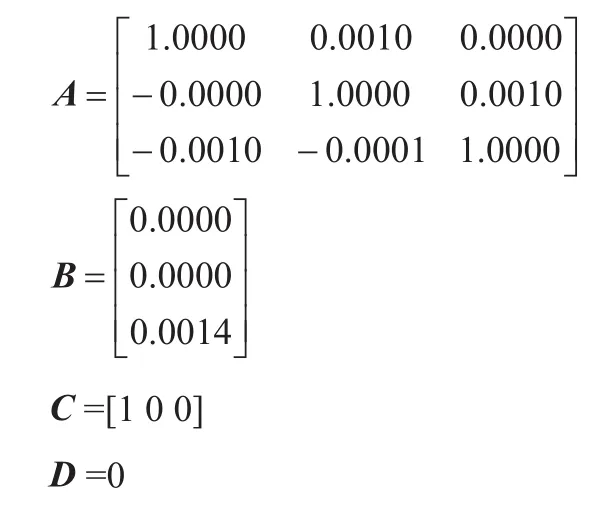
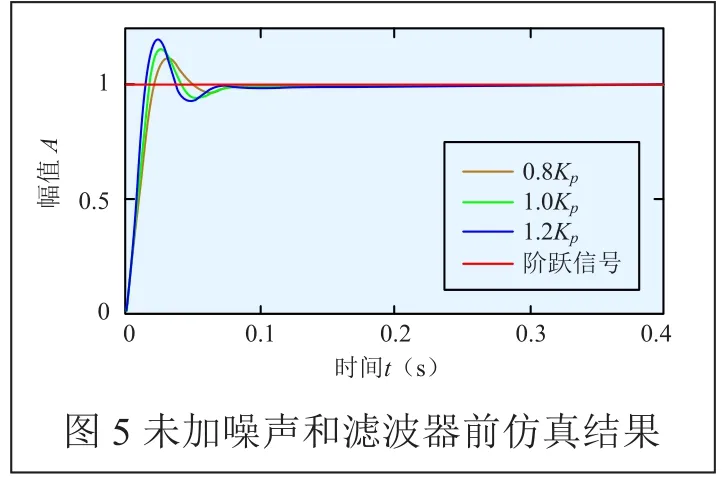
表1 系統動態響應特性

實驗噪聲大小情況如圖6所示。加入濾波器后仿真結果如圖7所示。由圖7可以得出，系統在加入噪聲和擾動后，未加入濾波器的動態響應特性，上升時間tr=0.0175s，系統加入干擾后，產生隨機抖動，無法達到穩定狀態，系統超調量σ%=22.5%；加入濾波器后的動態響應特性，上升時間tr=0.0175s調節時間ts=0.177s，系統超調量σ%=22.2%，系統在經過0.177s后達到穩定狀態，響應速度較快。

實際系統中，噪聲影響比實驗中要復雜的多，卡爾曼濾波器在實際應用效果中有一定偏差，但整體滿足到控制性能的要求。

五、結束語

本文主要以光電吊艙俯仰環為被控對象進行系統建模，通過改變系統增益大小，加入噪聲干擾等條件，采用基于卡爾曼濾波器的分數階PIλDμ控制方法與純分數階PIλDμ控制方法進行仿真對比研究，結果顯示系統未加入噪聲和濾波器前，純分數階PIλDμ控制器具有較強的增益魯棒性，加入噪聲和濾波器后，單純的分數階 PIλDμ控制器無法滿足系統要求。基于卡爾曼濾波器的分數階 PIλDμ控制器控制效果有明顯改善，滿足系統需求。