流媒體系統中內容分發網絡的服務器部署優化

徐錫健，鄔惠峰，吳海列

(杭州電子科技大學 計算機學院，浙江 杭州 310018)

0 引 言

近年來隨著流媒體的應用和普及，如何保證用戶體驗及降低成本成了研究熱點。袁小群等[1]提出并分析了服務器優化部署對流媒體系統的重要性。

內容分發網絡(content delivery network，CDN)被廣泛應用到流媒體的內容分發研究中。CDN網絡中服務器的放置至關重要，曾明霏等[2]就P2P服務器如何放置以滿足盡量多節點進行了研究，鄭晶晶等[3,4]分別提出分布式交互應用中服務器放置問題的模擬退火、禁忌搜索和改進遺傳算法的解決方案。此外，Hamid Jabraili等[5,6]也研究了服務器部署中提高延時性能，優化服務質量的啟發式算法。Darothi Sarkar等[7,8]調查了多種CDN網絡中副本服務器的放置算法并概括了他們的特點。時延性能是他們的主要研究問題，但是在流媒體CDN中，帶寬保證比時延更重要，只要能保證分發給用戶的流內容最低吞吐量，流媒體播放器的緩沖機制就能控制延遲抖動在一個有界范圍內，從而保證用戶體驗[9]。同時考慮時延性能和帶寬約束的數學模型太過復雜，不易處理，本文建立了考慮服務器部署成本、網絡租用成本、帶寬約束和用戶流量需求的MCMF(minimum cost maximum flow)模型[10]，并用模擬退火遺傳算法求解該模型，同時與文獻[10]中該問題的混合整數規劃模型求解結果進行了比較，確定了算法的可行性和有效性。

1 數學模型

1.1 問題描述

流媒體內容服務器部署問題可以描述為：在給定的網絡拓撲圖中，有N個網絡節點，其中有M個消費節點。從網絡結構模型中選擇一部分網絡節點，在其上一對一的部署流媒體內容服務器。提供的部署方案需要使得媒體流從內容服務器經過一些網絡節點和鏈路到達消費節點。兩個網絡節點之間最多僅存在一條鏈路，每條鏈路有相應的帶寬限制和單位帶寬租用費，求滿足所有消費節點的流量需求下總成本最低的服務器部署方案。

1.2 符號說明

設G=(V,E)為賦權圖，V={0,1,2,…,N-1}，{v0,v1,…,vn-1}為頂點集，E={e1,e2,…,en}為邊集，xi-j為節點vi和vj之間的鏈路總帶寬，wi-j為該鏈路的單位帶寬租用費，fi-j為從i到j的流量，每個服務器的部署成本是cost。為了符合MCMF模型，需要在圖上添加一個虛擬源節點和一個虛擬匯節點，源節點序號為N，與所有服務器節點相連，假設所有流量都從源節點輸出；匯節點序號為N+1，與所有消費節點相連，假設所有流量最終都傳輸到匯節點，設V’={0,1,2,…,N+1}{v0,v1,…,vn+1}為包含源匯節點的頂點集，以源節點和匯節點為端點的鏈路帶寬無限制，網絡租用費為0。對于第i個節點，設

(1)

設有M個消費節點的集合為VU={vu1,vu2,…vuM}，其中VU?V，每個消費節點的需求是NE={nu1,nu2,…,nuM}。

1.3 目標函數及約束條件

本文綜合考慮服務器部署成本，網絡租用費，鏈路帶寬限制，用戶流量需求，如下雙目標規劃模型

(2)

(3)

其中，pi表示第i個節點是否是服務器節點，約束條件1說明這是一個二值項，cost為每部署一個服務器的成本，wi-j與fi-j的乘積是一條鏈路的實際網絡租用費，條件2表示每條鏈路的實際流量不會超過該鏈路的流量上限，條件3表示每個消費節點的流量需求都恰好被滿足，條件4表示除了源匯節點的其它節點的流量入度和初度總和是相等的，以此確保從服務器輸出的流量能全部傳輸到消費節點。

原網絡拓撲圖的一個實例如圖1所示：正方形代表服務器節點，三角形代表消費節點，圓圈代表普通節點，鏈路上的標記(x,y)中，x表示鏈路總帶寬(單位為Gbps)，y表示每Gbps的網絡租用費(千元)。添加了源匯節點的網絡拓撲圖如圖2所示，流量從源點S出發經過若干服務器節點，普通節點和消費節點最終到達匯點E。

圖1 原網絡拓撲圖

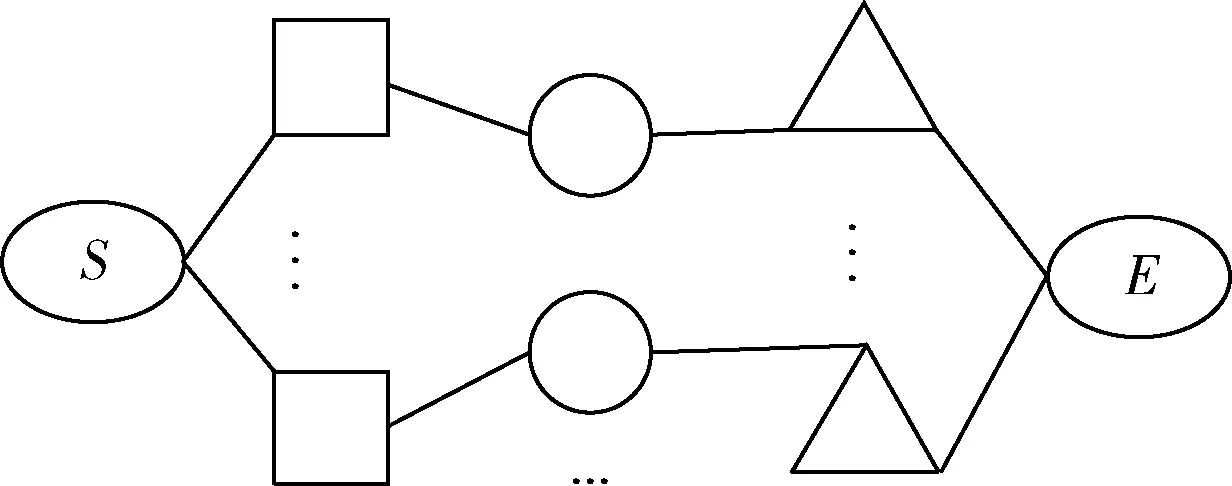
圖2 帶源匯節點網絡拓撲圖

2 算法設計

2.1 算法描述

本文提出的問題是一個多目標優化問題，相對于單目標優化，多目標的主要特征是權衡各個目標使其達到綜合的最優解，此類問題多采用啟發式算法解決，本文采用自適應模擬退火遺傳算法解決此問題。

2.1.1 遺傳算法

遺傳算法(genetic algorithm，GA)的定義請參見文獻[11]。遺傳算法的全局搜索能力強，但是存在早熟問題，詳情請參見文獻[12]，需要進行優化，因此本文根據適應度的變化，自適應地變化種群交叉概率pc和變異概率pm，而適應度的集中程度用最大適應度fitmax、最小適應度fitmin和適應度平均值fitave這3個變量來衡量。可以利用如下公式對pc和pm進行自動調整

(4)

(5)

實驗表明，本文的問題中a取0.78，b取0.66可以達到很好的效果。自適應遺傳算法雖然運行效率上比改進前算法有了顯著的提高，但其局部搜索能力還有改進空間。

2.1.2 模擬退火算法

模擬退火算法(simulated annealing)的定義及原理請參見文獻[13]。模擬退火算法的局部搜索能力強，但對于基本的模擬退火算法，在問題規模很大時想要得到一個高度接近最優解的結果需要花費的時間過長。

2.1.3 模擬退火遺傳算法

模擬退火遺傳算法是在遺傳算法的基礎上引進模擬退火思想的一種改進算法，能有效避免兩者的缺點，結合兩者的優點。模擬退火遺傳算法分內外兩層，外層從一個較高溫度開始逐漸下降，期間運行遺傳算法，內層進行子種群的尋優，當溫度到達下限或者連續若干代迭代的最優解一直沒有變化時，算法結束。

2.1.4 SPFA算法

SPFA算法是一種對任意有向圖求單源最短路徑的算法，夏正冬等對其正確性和效率都有分析[14]。本文的圖結構的鏈路中實際流量的流動方向是不確定的，因此若將一個方向作為正向，該邊就是正權邊，其反向邊就是負權邊，這時一些最短路徑算法如Dijkstra算法等就無法處理了，而Bellman-Ford算法的復雜度過高，因此本文選用了SPFA算法。

2.2 算法實現

2.2.1 編碼

遺傳算法將實際問題抽象成染色體編碼的方式進行求解，每一條染色體對應一個該問題的解決方案。遺傳算法的編碼方式有多種，本文采用二進制編碼，一條染色體是一條0/1序列，分別對應非服務器節點和服務器節點兩種情況，序列下標代表網絡節點序號。

2.2.2 產生初始種群

初始種群是利用隨機數函數生成若干條染色體組成的，種群規模跟網絡節點個數存在一定聯系，起初網絡節點越多，種群規模越大，隨著網絡節點不斷增多，計算單個染色體方案的路徑搜索耗時急劇增加，此時需要減小種群規模以保持迭代速度。初始種群可表示為A={X1,X2,…,Xn},其中Xi是種群中的第i條染色體。

2.2.3 適應度函數設計

針對本文多目標優化求最小代價問題，代價越高，個體適應度越差，同時為了提高算法效率，將代價設置上界，當且僅當在所有消費節點都部署服務器時，代價達到可接受的最大值max，此時所有消費節點的流量需求都被滿足，再增加一個服務器都是多余的，適應度函數構造如下

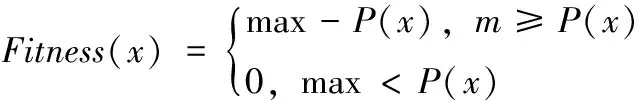
(6)

其中，P(x)為當前方案的代價。

2.2.4 選擇

每次迭代需要從種群中挑選出適應度高的個體用以進行后續操作。本文采取的選擇策略是錦標賽選擇法，每次從種群中隨機抽出兩個個體，適應度較大者遺傳到下一代，另一個個體以模擬退火的方式按一定的概率接受，這個概率為

(7)

式中：dE是適應度的變化量(負數)，取該個體的適應度與fitmax的差值，與fitmax相差越小，表示該個體適應度較優，P(dE)越大，由于dE總是小于0，所以P(dE)取值在0到1之間。k為常數，T表示溫度，為正數，設定初始值后，迭代過程中T按一定比率降低，算法初期溫度高，P(dE)一般較大，保持種群多樣性，后期溫度低，P(dE)小表示種群靠近最優解鄰域，逐漸穩定。

2.2.5 自適應交叉

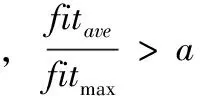
2.2.6 自適應變異

模擬退火遺傳算法的基本流程如圖3所示。

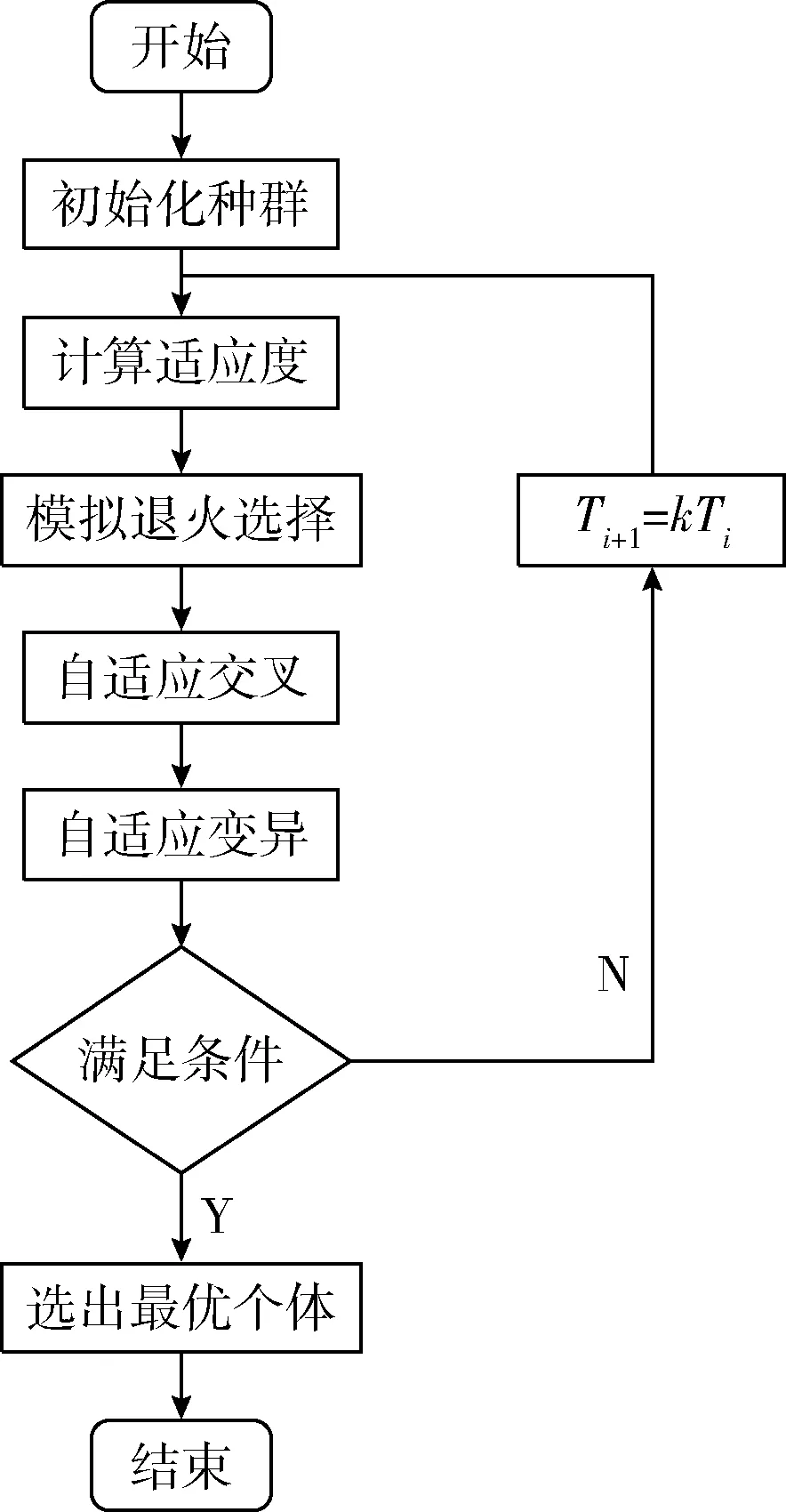
圖3 模擬退火遺傳算法流程

2.3 MCMF模型與SPFA算法

遺傳算法過程中計算個體適應度的時候需要根據服務器的分布狀況確定網絡中各節點間的流量大小和流向，使得網絡租用費最小，這是一個MCMF問題，尋路過程中存在負權邊，因此選用SPFA算法。

2.3.1 MCMF問題求解

MCMF問題是結合網絡流的費用和流量問題，尋找最優解的問題[16]，在一個網絡的每段路徑都受容量和費用限制的條件下，該模型試圖計算出從一個點到另一個點的流量最大，費用最小的解決方案。本文中，MCMF的實現步驟如下：

步驟1 初始化圖中所有邊xi-xj之間的當前流為0,xi,xj為圖中任意連通的兩個點，初始化每條邊的剩余流量帶寬bw，費用流總代價totalCost和當前流大小為0。

步驟2 調用SPFA算法搜尋到一條從起始節點S到終止節點E的增廣路徑，按順序記錄路徑上從S到E的網絡節點{x0x1…xi…xj}，若找不到增廣路徑，跳到步驟4。

步驟3 從步驟2中記錄的路徑中找出限制可行流大小的關鍵邊xi-xi+1，若此邊的當前流為負，則以此當前流的絕對值作為這條路徑可行流的大小minf，否則，以此路段的剩余流量帶寬bwi-(i+1)作為這個可行流的大小minf。修改殘留網絡信息并更新totalCost和currentFlow。

步驟4 重復步驟2和步驟3，直到找不到新的增廣路徑為止。此時若所有消費節點需求都被滿足，則方案合法，否則非法。

2.3.2 SPFA算法實現

求解過程中的尋路算法采用SPFA算法，該算法可分為初始化和松弛兩步操作，其實現步驟為：

步驟1 初始化。建立源點S到圖中各點的距離數組distSPFA[N+1]，S到本身距離為0，到其它所有點距離初始化為正無窮。然后建立訪問數組visited[N+1]，表示一個節點是否正在隊列中，每個元素都初始化為false。路徑記錄數組parentSPFA[N+1]用于記錄每個節點在路徑中的前驅節點，所有元素初始化為-1。建立一個隊列queue，初始時隊列里只有源點S。進隊次數記錄數組enterQueueCount[N+1]用于記錄每個點的進隊次數，所有元素初始化為0。

步驟2 松弛操作。queue非空時，隊首元素i出隊，對以i為尾節點的所有邊ei,j的頭結點進行松弛操作：若distSPFA[i]+ei,j比distSPFA[j]小，則將前者賦值給后者，若j不在隊中，則j入隊，其入隊次數enterQueueCount[j]加1，記錄路徑中j點的前驅為i，parentSPFA[j]=i，visited[i]設為1。若隊列為空，結束算法。

2.4 實例分析

圖4是一個實例的網絡拓撲圖。

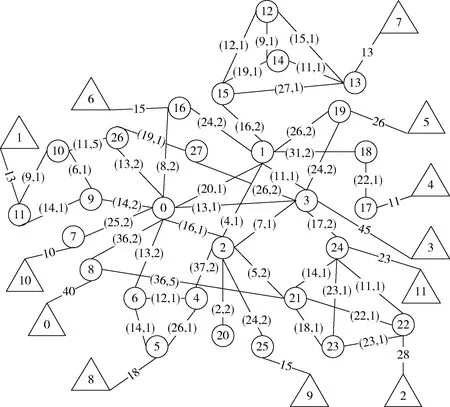
圖4 實例網絡拓撲圖

圖4中圓圈為網絡節點，三角形為消費節點，網絡節點間鏈路上的標記(x,y)如章節1.3所述。每個消費節點只與一個網絡節點直接相連，其對應的鏈路帶寬租用費為0，鏈路上的數據表示該消費節點的帶寬需求。本文算法需要從網絡節點中選出部分節點部署服務器，以滿足所有消費節點的帶寬需求，同時使服務器部署成本及網絡租用成本之和達到最小。

以上網絡拓撲結構以文本文件形式記錄下來作為程序的輸入，文件格式如下：

網絡節點數x1 網絡鏈路數x2 消費節點數x3

單個視頻內容服務器部署成本

鏈路起始節點ID鏈路終止節點ID總帶寬 租用費

……(如上鏈路信息x2-1條)

消費節點ID相連網絡節點ID視頻帶寬消耗需求

……(如上消費節點信息x3-1條)

以圖4為例其輸入文件形如：

28 45 12

100

0 16 8 2

……(如上鏈路信息44行)

26 27 19 1

……(如上消費節點信息11行)

由于輸入文件篇幅過長，部分相似信息省略。文件輸出格式如下：

網絡路徑數Line

(空行)

從服務器節點到消費節點的路徑路徑所占帶寬

……(如上路徑信息Line-1條)

cost:成本(千元)

算法耗時(毫秒)

圖4實例的解決方案如圖5所示。

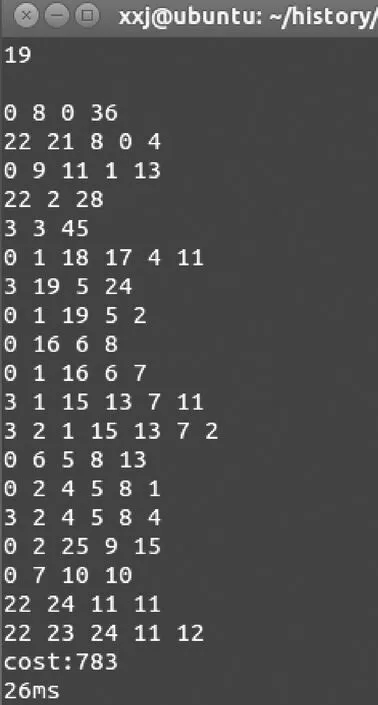
圖5 解決方案

解決方案給出19條路徑，對應圖5中的19行輸出路徑，每行第一個數據是服務器節點序號，后跟若干普通網絡節點序號，倒數第二個數據是消費節點序號，最后一個數據是該條路徑所占帶寬。從圖5中第3,4行可以看出，0號消費節點的帶寬需求可由0號和22號服務器節點滿足，帶寬路徑為0->8->0(分配了36 Gbps)和22->21->8->0(分配了4 Gbps)，其它消費節點以此類推，如圖6所示，0,3,22號網絡節點為服務器節點，它們滿足了所有消費節點的帶寬需求，刪去不必要的鏈路，剩下每條鏈路都標明了帶寬大小和方向。該方案成本為783(千元)，算法耗時26 ms。

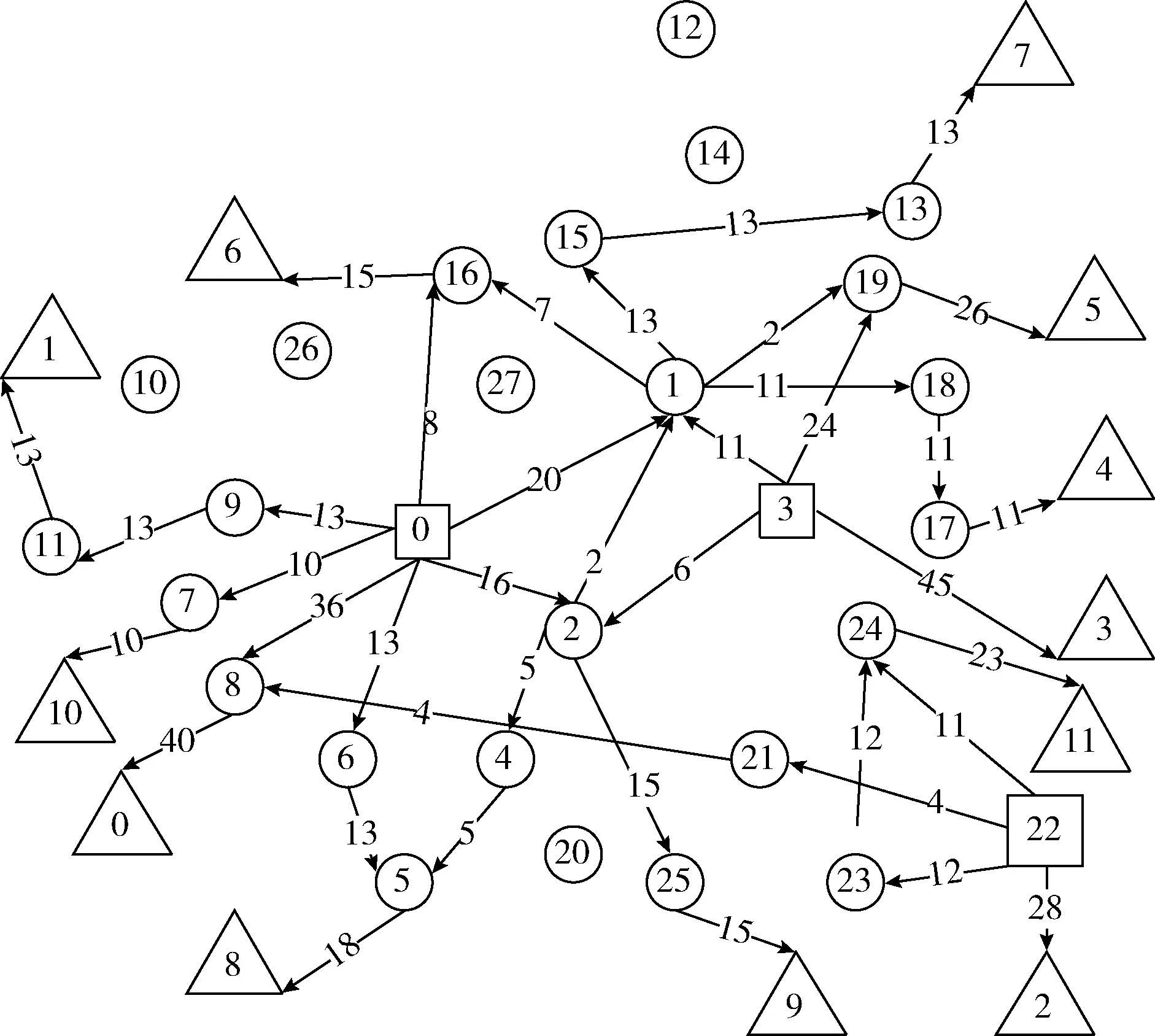
圖6 解決方案

3 實驗與結果分析

3.1 實驗環境

本文使用的編程語言是C++，仿真環境如下：

CPU：intel(R) Core(TM) i3 CPU 550 @ 3.20 GHz 3.19 GHz

內存：2.00 GB

內核：單核

編譯器：gcc 4.8.4

操作系統：linux Ubuntu 14.04.4 LTS 64位，內核版本Linux version 4.2.0-27-gineric

為了保證客觀性和普適性，本文的實驗數據來自第三屆華為軟件精英挑戰賽提供的案例。

3.2 實驗步驟

(1)輸入：算法需要的輸入數據從文件中讀取，文件格式請參見2.4節，本次實驗采用了4組不同規模的用例，分別是初級用例：50個網絡節點，97條網絡鏈路，9個消費節點；

低級用例：160個網絡節點，606條網絡鏈路，72個消費節點；

中級用例：300個網絡節點，1134條網絡鏈路，135個消費節點；

高級用例：800個網絡節點，2939條網絡鏈路，360個消費節點。

(2)輸出：實驗結果輸出到文本文件中，文件格式請參見2.4節。

(3)結果分析：對上述多個案例的實驗結果進行統計，并將計算結果與文獻[9]提出的混合整數規劃模型的計算結果進行性能比較。

3.3 仿真結果對比與分析

在不同規模下計算出的部署方案總成本(千元)和消耗的時間(ms)見表1和表2。

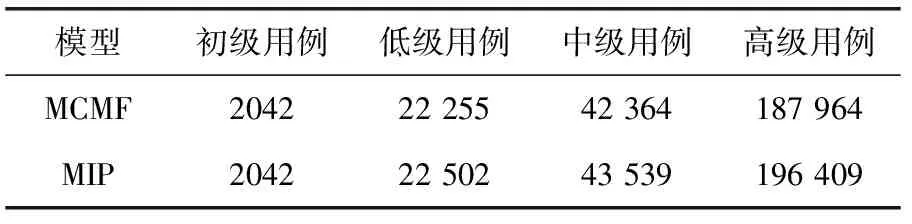
表1 兩種模型在不同規模用例下的成本

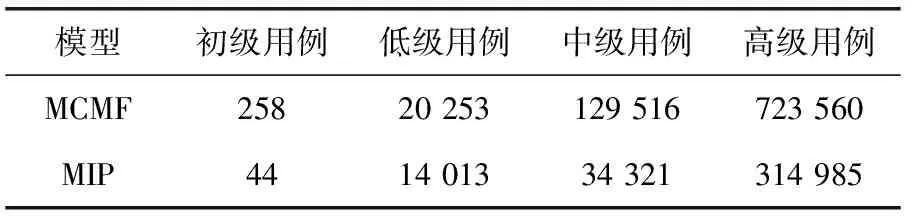
表2 兩種模型在不同規模用例下的耗時

由表1可以看出，初級，低級，中級，高級用例中MCMF模型分別比MIP模型減少了0%，1.1%，2.7%，4.3%的成本。可見對于小規模用例，前者與后者求取的最優解相差不大，隨著規模的增加，MCMF的優勢越趨明顯，這個由圖7更能直觀地表現出來。

由表2可以看出，MCMF模型耗時比MIP模型多，這是因為前者求解最優解使用了模擬退火遺傳算法，為了避免過早陷入局部極值，后期繼續搜尋全局最優解而耗時增加，而后者在算法后期最優解成本已沒有下降的空間。

圖7 兩種模型在不同規模下代價比較

圖8為兩種模型在相同規模案例的運算過程中成本隨著時間變化的曲線。可以看出兩者在算法前期尋找更優解的效率很高，隨著當前最優解越來越接近全局最優解，效率逐漸降低。圖中t時刻MCMF模型的代價有個小幅的下降，這是因為算法在尋優過程中跳出了某個局部極值，成功避免了早熟現象，而MIP模型無法尋找到更優解，過早地結束了算法，這與表1和表2的記錄相吻合。

圖8 代價-時間變化

4 結束語

本文基于流媒體服務器部署問題中服務器數量和位置不確定性，以及網絡結構中每條鏈路都有帶寬和租用費雙重限制的特性，將多源點多匯點的網絡結構改造成單源單匯的結構，建立了MCMF模型。設計了模擬退火遺傳算法求解該問題，并與前人提出的基于MIP模型的貪婪分解算法進行比較。實驗結果表明，該模型在求解最優解方面勝過MIP模型，用例規模越大，前者的該項優勢越明顯，作為代價，算法耗時有所增加，因此在算法效率方面有待進一步研究。