改進CUSUM算法的工控系統(tǒng)入侵檢測方法

魏戰(zhàn)紅，王展鵬，王 安，宋玉寶，趙國新

(1.北京石油化工學院 信息工程學院，北京 102617；2.北京化工大學 信息科學與技術(shù)學院，北京 100029；3.北京郵電大學 網(wǎng)絡與交換技術(shù)國家重點實驗室信息安全中心，北京 100876)

0 引 言

針對工業(yè)控制系統(tǒng)(industrial control system，ICS)面臨的信息安全威脅[1-5]，入侵檢測系統(tǒng)可以有效監(jiān)控系統(tǒng)的運行狀態(tài)，檢測入侵行為，為下一步采取安全應對措施，提供依據(jù)[6,7]。

入侵檢測在ICS環(huán)境有如下特殊要求：不能影響ICS本身的可用性、穩(wěn)定性[8]；實時性高，檢測速度快[9]；ICS節(jié)點的CPU計算能力往往較弱，檢測算法需要簡單高效[10]。針對以上要求，CUSUM(cumulative sum)算法檢測速度快，計算簡便，適用于ICS。CUSUM算法不斷改進，李等[11]使用柯爾莫哥夫不等式對CUSUM偏移常數(shù)β進行改進。周[12]提出了基于變點CUSUM方法的正態(tài)過程方差的CUSUM控制圖，在檢測大漂移上效率高。張[13]針對非參數(shù)CUSUM算法，設計了自適應偏移常數(shù)β。但是目前的研究往往不能滿足ICS高可用性、高實時性、高檢測速度的要求。

本文分析了ICS特點，改進了CUSUM算法，給出了一個基于改進CUSUM算法新的入侵檢測方法。該方法首先以傳感器獲取的實際值和模型的預測值之間的差值為統(tǒng)計序列。然后根據(jù)3σ原則設計偏移常數(shù)β，并決定門限值τ的取值。最后使用偏差攻擊和幾何攻擊對該入侵檢測方法進行實驗，驗證改進的CUSUM算法能夠準確快速地檢測出入侵，其誤報率較低，適用于ICS環(huán)境。

1 ICS入侵模型

當ICS被攻擊時，被攻擊的傳感器測量信號y′將出現(xiàn)偏差。若y′超過上下限，將檢測到異常，觸發(fā)上下限報警。若y′仍然在上下限范圍內(nèi)，測量值如下

(1)

式中：Ka表示被攻擊的時間序列，ai(k)是被攻擊時的測量值，其仍在上下限范圍內(nèi)。ICS中被控對象的輸入uk決定了輸出y(k)。給定被控對象的輸入uk，通過下式ICS模型可求得期望輸出

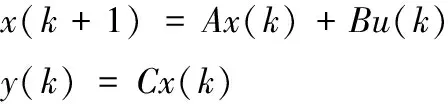
(2)

式中：x(k)=(x1(k),…,xn(k))為k時刻系統(tǒng)輸入，y(k)=(y1(k),…ym(k))為k時刻傳感器的測量值，矩陣A為狀態(tài)矩陣，矩陣B輸入矩陣，C為輸出矩陣。

2 改進CUSUM入侵檢測方法

2.1 CUSUM算法

CUSUM算法是一種變化檢測方法，它可以檢測到統(tǒng)計過程均值的變化。CUSUM算法原理是：如果從某點開始有異常出現(xiàn)，則序列的概率分布會發(fā)生改變。整個數(shù)列的均值或者方差也發(fā)生變化，可判定從該點起為異常。

假設變量x，在無攻擊的正常時刻，其統(tǒng)計分布概率為P0，攻擊發(fā)生后，其統(tǒng)計分布概率為P1。CUSUM算法中N為停止時間，S為累加和。假設S(0)=0，則有

(3)

函數(shù)a為

(4)

停止時間N為

N=inf{n:S(n)≥τ}

(5)

式中：inf為下確界，取滿足條件的最小值。檢測的判定公式

(6)

d(N)用于判斷檢測序列是否發(fā)生變化，τ作為判定入侵的門限值。在n時刻，S(k)>τ，則檢測到異常，發(fā)出警報。可以看出，CUSUM算法將變化檢測問題轉(zhuǎn)化為S(k)和τ的大小比較問題。報警門限值τ決定誤報率，τ越小，誤報率越高，檢測性能越靈敏。

當CUSUM算法用于ICS入侵檢測時，存在一定的局限性：由于log[p0(x(k))/p1(x(k))]計算復雜，占用CPU資源較多，很難獲得統(tǒng)計分布概率P0、P1。而且ICS中各節(jié)點CPU能力較弱，使得檢測時間較長，無法滿足ICS入侵檢測對高實時性的要求。

2.2 改進CUSUM算法

(7)

正常狀態(tài)下，傳感器測量值與預測值幾乎相同，差值Δk是一組接近于0的序列；當攻擊發(fā)生時，Δk將產(chǎn)生較大變化。Δk與log[p0(x(k))/p1(x(k))]有相似的變化，可將log[p0(x(k))/p1(x(k))]簡化為差值Δk。

根據(jù)CUSUM算法要求，正常狀態(tài)下，需要S(k)<0；攻擊發(fā)生后，需要S(k)>0。所以引入一個正值常數(shù)β，讓大部分Δk-β<0，定義

x(k)=Δk-β

(8)

x(k)作為被檢測序列，β是一個比較小的正值常數(shù)，使得在正常狀態(tài)下，期望E(x(k))<0；在攻擊發(fā)生后，期望E(x(k))>0。累加和S(k)計算如下

(9)

根據(jù)式(4)定義的函數(shù)a+，式(9)中累加和S(k)只累計x(k+1)+S(k)為正的值，所以正常狀態(tài)下，S(k)=0。攻擊發(fā)生時，Δk變大，x(k)>0，S(k)開始累加。

根據(jù)式(6)，當S(k)>τ時，判別函數(shù)d(N)=H1，表示系統(tǒng)處于被攻擊狀態(tài)；S(k)≤τ時，d(N)=H0，表示系統(tǒng)處于正常狀態(tài)。τ越小，約束越嚴格，檢測時間越短，越容易誤報。

2.3 參數(shù)選取

算法參數(shù)β和τ的取值直接影響檢測算法的性能。液位控制系統(tǒng)的液位量在正常運行時，預測值Δ和測量值y的差值Δk符合正態(tài)分布，則Δk在(μ-3σ,μ+3σ)中的概率為0.9974(μ為期望，σ為標準差)。式(8)中x(k)的期望值需要滿足E(x(k))<0，假設β取值為3σ，則x(k)=Δk-β<0的概率為0.9974，期望E(x(k))<0。

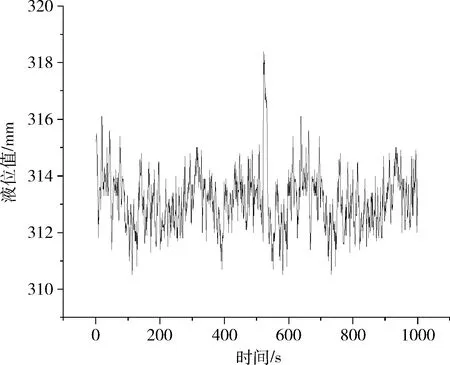
圖1 液位測量值分布

圖2 測量值與預測值的差值分布

τ為報警門限值，若S(k)>τ，則檢測出異常。τ越小，S(k)越快到達τ報警門限值，檢測時間N越短，其誤報率越高(液位控制系統(tǒng)的要求液位320 mm以內(nèi)，在此偏差內(nèi)報警屬于誤報)。τ的取值要綜合考慮檢測時間和誤報率。在正常狀態(tài)下，檢測系統(tǒng)根據(jù)不同的τ值計算誤報率。如圖3所示，在τ值為19.8時，誤報率為0.1%，理論上取τ值為19.8，即可保持低誤報率。

由于S(k)與采樣周期有關(guān)，如果采樣周期很小，即使小偏差也可以使S(k)很大。本系統(tǒng)選用1 s的采樣周期，采用比例攻擊仿真來選擇τ值。τ取值與檢測時間關(guān)系如圖4所示，檢測時間隨τ變大而變長。τ取值19.8時，檢測時間為5 s。對于液位控制系統(tǒng)，5 s的檢測時長滿足要求。綜合考慮了檢測時間和誤報率后，選取τ值為19.8。

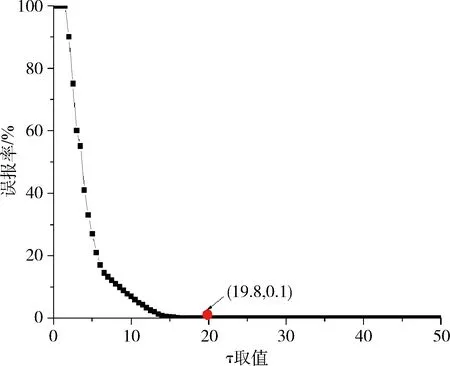
圖3 τ取值與誤報率關(guān)系

圖4 τ取值與檢測時間關(guān)系

3 方法檢驗和結(jié)果分析

通過模擬攻擊者對控制系統(tǒng)攻擊，檢驗改進CUSUM入侵檢測方法的性能。攻擊目標是液位傳感器，使用欺騙手段，對傳感器測量值進行修改。

3.1 偏差攻擊

偏差攻擊是指傳感器測量值y(k)被引入了偏差δ(偏差不足以觸發(fā)上下限報警)，使得控制效果不理想，甚至造成現(xiàn)場危險。液位傳感器的正常范圍在[0,320]，超過320 mm觸發(fā)上限報警。加入偏差δ后，液位傳感器值為

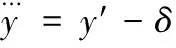
(10)

使用Matlab進行仿真攻擊，使用不同δ值，先討論在上升期的情況下。上升期，罐內(nèi)進行注水操作，液位不斷升高至設定值313 mm。攻擊者對液位傳感器使用偏差攻擊，偏差攻擊值δ分別取0、5、30、100，時間范圍[0,1200]。偏差攻擊下的液位曲線如圖5所示，偏差攻擊使液位無法到達設定值，設定值和實際值的差值即為δ值。攻擊危害出現(xiàn)時刻是液位到達篡改值的時刻(即設定值減去攻擊偏差δ值)。攻擊下液位與預測液位之間的差值曲線如圖6所示，從攻擊威脅出現(xiàn)時刻起，差值Δk開始變大，直到Δk=δ。當Δk>β后，S(k)開始累加。在偏差攻擊δ值分別取0、5、30、100時，改進CUSUM算法檢測時間見表1。當δ=0時，相當于沒有攻擊，是系統(tǒng)正常狀態(tài)；當δ=5時，在641 s實際值與預測值產(chǎn)生偏差，偏差攻擊開始產(chǎn)生威脅，檢測系統(tǒng)在649 s處報警，檢測時間為8 s；當δ=30時，檢測時間為5 s；當δ=100時，檢測時間為2 s。結(jié)果表明，在上升期改進CUSUM算法對偏差攻擊檢測有效，攻擊幅度越大，檢測越迅速。

圖5 偏差攻擊下的液位曲線(上升期)

圖6 預測值與實際值的差值曲線(上升期)

平穩(wěn)期，罐內(nèi)液位保持在313 mm微小波動，在平穩(wěn)狀態(tài)下，從800 s開始，攻擊者對液位傳感器使用偏差攻擊δ，δ分別為0、5、30、100。偏差攻擊下的液位曲線如圖7所示，偏差攻擊使液位快速下降，攻擊發(fā)動便開始產(chǎn)生威脅，液位將偏離原定的設定值。圖8表示攻擊下實際值與預測值之間的差值曲線，從攻擊產(chǎn)生危害開始，Δk迅速變大，直到Δk=δ。改進CUSUM算法檢測時間見表2。當δ=0時，相當于沒有攻擊，是系統(tǒng)正常狀態(tài)，沒有報警；當δ=5時，在800 s實際液位與預測值產(chǎn)生偏差，偏差攻擊開始產(chǎn)生危害，檢測系統(tǒng)在806 s處報警，檢測時間為6 s；當δ=30時，檢測時間為3 s；當δ=100時，檢測時間為2 s。結(jié)果表明，在平穩(wěn)期改進CUSUM算法對偏差攻擊檢測有效，檢測速度快。

表1 偏差攻擊下的報警時間(上升期)

圖7 攻擊下的液位曲線(平穩(wěn)期)

圖8 預測值與實際值的差值曲線(平穩(wěn)期)

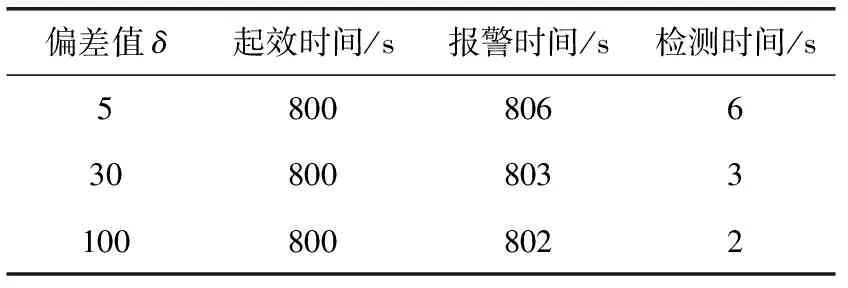
表2 偏差攻擊下的報警時間(平穩(wěn)期)

3.2 幾何攻擊

幾何攻擊具有初始變化緩慢不易偵查，一段時間后幾何式爆發(fā)的特點，對工業(yè)控制系統(tǒng)造成巨大影響。幾何攻擊可以表示為

(11)

nk時，攻擊呈幾何式增長。選定參數(shù)η=1.8,γ=0.75,k=10。幾何攻擊下的液位如圖9所示。

圖9 幾何攻擊下液位實際值分布

攻擊從10 s開始產(chǎn)生威脅，改進CUSUM在15 s報警，檢測時間為5 s；液位上限報警在19 s觸發(fā)，歷時9 s。在幾何攻擊下改進CUSUM算法5 s便能快速做出反應，檢測速度較快。

4 結(jié)束語

工業(yè)控制系統(tǒng)的入侵檢測有高可用性、高實時性的要求。針對工業(yè)控制系統(tǒng)的特點，提出了一種基于改進CUSUM算法的ICS入侵檢測方法。該方法以模型預測值與實際測量值之間的差值作為檢測序列，根據(jù)3σ原則設計偏移常數(shù)β，并決定門限值τ的取值。通過偏差攻擊和幾何攻擊實驗，檢驗改進CUSUM入侵檢測方法性能。實驗結(jié)果表明，改進CUSUM入侵檢測方法檢測時間較短，誤報率低，檢測率高，在工業(yè)控制系統(tǒng)入侵檢測中有實際應用價值。由于β參數(shù)和門限值τ與誤報率、檢測時間、檢測率相互關(guān)聯(lián)，進一步優(yōu)化對參數(shù)的選取，是接下來的研究方向。