(n,1,L)卷積碼的邏輯運算譯碼方法
楊雪梅,畢春艷
(四川大學錦江學院 電氣與電子信息工程學院,四川 眉山 620860)
0 引 言
卷積碼是1955年由Elias等人提出的。在設備復雜度相同的條件下,它的性能優于分組碼,糾錯能力隨約束長度的增加而增強[1-2]。目前,卷積碼最實用的(n,k,L)卷積碼是k=1的(n,1,L)卷積碼[3],已廣泛應用于實際通信系統中,如2G、3G和商業衛星通信系統等。例如,為了實現前向差錯控制,GSM移動通信系統在下行和上行鏈路中都采用了(2,1,5)卷積碼,IS-95 CDMA系統在下行鏈路中采用(2,1,9)卷積碼,而上行鏈路中采用(3,1,9)卷積碼。
常用的卷積碼譯碼方法還有Viterbi譯碼[4]。但是,隨著約束長度的增大,它的算法和硬件實現復雜度也會增加。此外,還有序列譯碼[5]和門限譯碼[6],但性能都較Viterbi譯碼差。文獻[7]提出了一種邏輯代數譯碼算法,但需要將錯誤類型分類討論。本文為(n,k,L)卷積碼設計了一種基于邏輯運算的譯碼方法,原理簡單,適合于所有(n,1,L)卷積碼的譯碼。
1 卷積碼的編譯碼原理
1.1 編碼原理
一個(n,k,L)卷積編碼器由 L·k-1級移位寄存器和n個模2和加法器(異或門)構成的輸出發生器組成[3]。每輸入k比特,編碼輸出一個n比特碼字,如圖1所示。
一個典型的(2,1,3)卷積碼的原理圖如圖2所示,連接矢量為G1=(111)2和G2=(101)2。
(2,1,3)卷積碼的兩個異或門的編碼輸出邏輯表示式為:
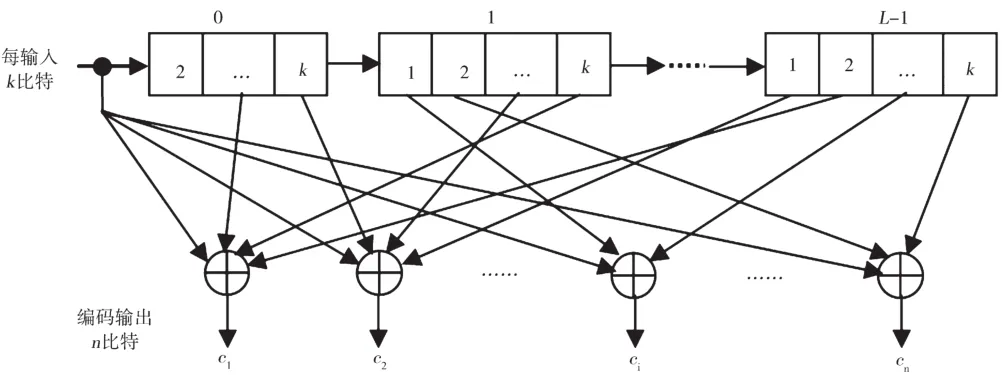
圖1 (n,k,L)卷積碼編碼器

圖2 (2,1,3)卷積碼編碼器
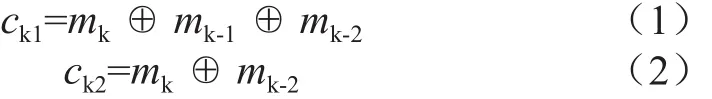
可見,輸入1位數字信號,可以得到2位卷積碼輸出數據。
(3,1,9)卷積碼連接矢量和異或門的編碼輸出邏輯表示式為:可見,輸入1位數字信號,可以得到3位卷積碼輸出數據。
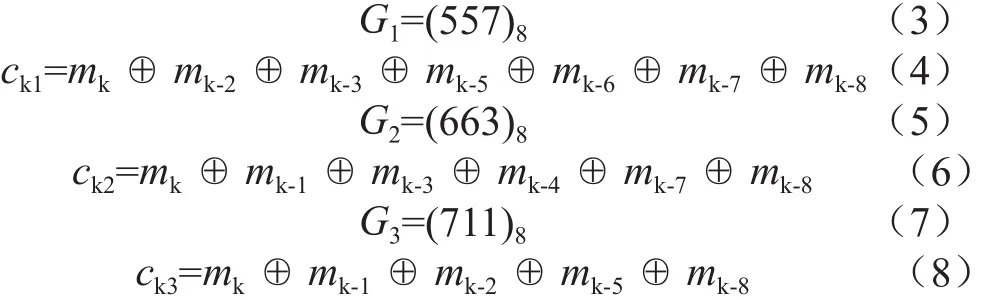
1.2 基于邏輯運算的譯碼原理
卷積碼譯碼過程中,不僅要從現在時刻收到的碼組中提取譯碼信息,而且要從以前或以后的多個時刻(與約束長度有關)收到的碼組中提取有關信息并糾錯。
目前,卷積碼譯碼方法有很多,可以分為兩大類:一類是是門限譯碼[5],另一類是基于最大似然原理的譯碼,包括Viterbi譯碼[4]和序列譯碼[6]。
邏輯運算的算法原理主要是根據異或運算的因果互換關系進行編碼逆運算從而實現譯碼,屬于最大似然譯碼。
以(2,1,3)卷積碼為例,它的譯碼器結構如圖3所示。
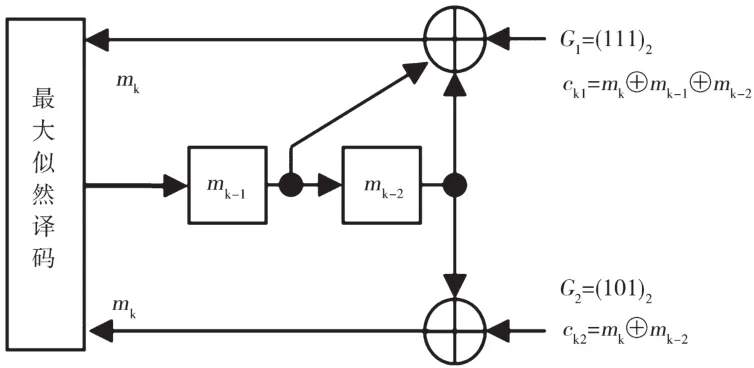
圖3 (2,1,3)卷積碼的譯碼器
利用異或運算的可逆性,由編碼方程式可得計算重建信息碼元mk的譯碼方程:

可見,異或逆運算后有2個mk。若2個mk相同,則譯碼正確;若不同,表明接收到的子碼ck有錯,或前面某一次譯碼中mk-n可能出現誤碼。此時,需檢查可能情況進行糾錯和判決,排除錯誤,最終確定輸出譯碼值。其中,糾錯和判決的思想采用擇優保留的原則。因此,譯碼器中異或門的輸出最終會進入最大似然譯碼算法進行判決,實現最終的譯碼。
同理,(n,k,L)卷積碼有n個碼采用邏輯運算譯碼后會得到n個mk。若n個mk相同,則譯碼正確;若不同,根據最大似然思想進行判決,實現譯碼。在隨機錯誤干擾下,發送的編碼信號不容易成片出現。n越多,越有利于使用最大似然算法進行譯碼,譯碼糾錯越容易,出現誤碼的幾率相對減小。
例如,在(3,1,9)卷積碼中,在進行邏輯運算譯碼后得到3個mk,根據最大似然思想,有:
(1)若有3個mk相同,則判決該mk為譯碼值;
(2)若3個mk不相同,此時可能出現錯誤。為了避免誤碼,需假設不相等位置的mk情況繼續譯碼,選擇誤碼最優的結果;
若在接收子碼ck中有連續2個以上錯誤,則譯碼可能出現誤碼,但后續譯碼也可進一步發現誤碼,此時需要通過相關算法進行糾正。
2 實現與仿真
通過卷積碼編碼方程,利用matlab仿真平臺得到其發送子碼。若發送信號序列為110100111,如表1所示。
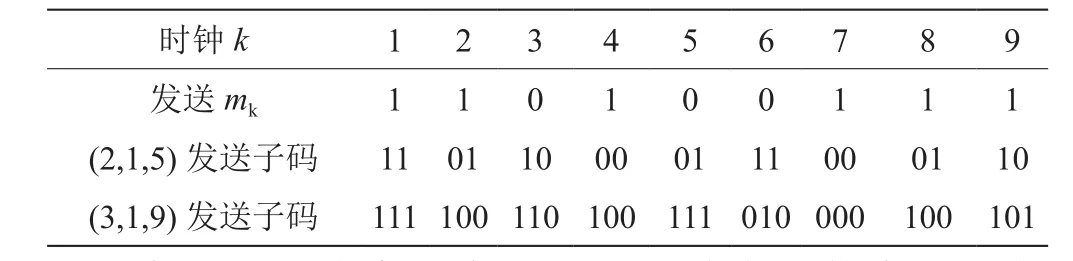
表1 編碼舉例
在matlab仿真平臺上,對幾種常用的卷積碼如(2,1,5)、(3,1,9)等基于邏輯運算譯碼進行仿真,并通過高斯白噪聲信道隨機加錯,檢查其誤碼特性。譯碼流程圖如圖4所示。
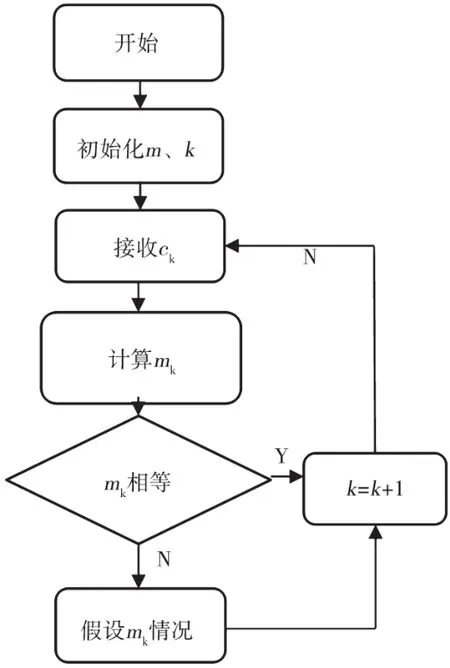
圖4 (n,1,L)卷積碼邏輯運算譯碼流程
隨機產生一串二進制數字序列,測試長度為1 000,在不同信噪比SNR下,(2,1,5)和(3,1,9)卷積碼的誤碼率如表2所示。
由表2可知,(2,1,5)和(3,1,9)卷積碼均能在邏輯運算譯碼方法下實現譯碼。約束長度不同,檢錯糾錯能力也有所不同。但是,算法或程序尚存在不成熟之處,需進一步研究改進性能。

表2 SNR與誤碼率對照表
3 結 論
利用邏輯異或運算的可逆性,將接收子碼與移位寄存器中數據根據編碼規則進行異或逆運算,得到n個發送數據,并根據最大似然思想完成對(n,k,L)卷積碼的邏輯運算譯碼功能,并通過matlab仿真驗證了其功能。該算法簡單,容易實現,對(n,k,L)卷積碼n>2時均適用。

