基于ELM神經(jīng)網(wǎng)絡的磷酸鐵鋰電池SOC估算研究

孫弘利，趙冠都

（中國海洋大學，山東 青島 266100）

0 引 言

AUV電源管理系統(tǒng)主要負責為AUV整體供電，保證AUV內(nèi)部各個系統(tǒng)模塊正常工作。磷酸鐵鋰電池是AUV的主要能源。因此，準確可靠地獲得磷酸鐵鋰電池SOC是AUV電源管理系統(tǒng)的基本任務之一。電池SOC能夠直接反映AUV內(nèi)部電池的總電量和AUV整體正常工作時間。人工神經(jīng)網(wǎng)絡很適合用于對多變量的電池SOC進行估算。

1 電池SOC估測方法

目前，對磷酸鐵鋰電池SOC的估算方法有開路電壓法、安時積分法和卡爾曼濾波法等。開路電壓法通過建立開路電壓（OCV）與SOC之間的關系，測量電池兩端的開路電壓值得到電池SOC，但是測得的SOC值往往需要將電池靜置較長時間，因此實現(xiàn)電池SOC的在線估算較困難。安時積分法是指在電池充放電過程中按時間對電流進行積分估算，在短時間內(nèi)能比較準確地得到估算結(jié)果，但是存在累積誤差問題。利用卡爾曼濾波法可得到SOC的最優(yōu)估算值和SOC的最優(yōu)值誤差，比較適合電池SOC估算，但是其依賴合適的數(shù)學模型，確定電池內(nèi)部參數(shù)困難[1-3]。本文采用ELM神經(jīng)網(wǎng)絡方法進行AUV內(nèi)部電池SOC模型建立，以估算AUV內(nèi)部電池SOC值。

2 神經(jīng)網(wǎng)絡的電池SOC模型建立

2.1 ELM神經(jīng)網(wǎng)絡結(jié)構(gòu)

ELM（Extreme Learning Machine）神經(jīng)網(wǎng)絡與其他神經(jīng)網(wǎng)絡（BP神經(jīng)網(wǎng)絡、支持向量機等）相比，訓練速度快，人工干擾少，網(wǎng)絡結(jié)構(gòu)簡單，泛化性能好，對于異質(zhì)性數(shù)據(jù)集泛化能力較強，很適合數(shù)據(jù)量相對少的訓練[3-6]。針對電池SOC的特性來說，很適合用ELM網(wǎng)絡。

ELM神經(jīng)網(wǎng)絡可理解為單隱層神經(jīng)網(wǎng)絡，結(jié)構(gòu)如圖1所示。

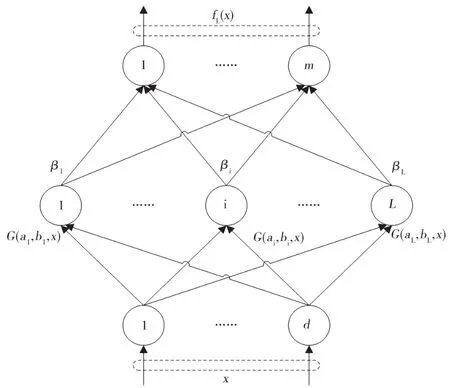
圖1 ELM神經(jīng)網(wǎng)絡結(jié)構(gòu)

像其他神經(jīng)網(wǎng)絡一樣，ELM網(wǎng)絡同樣含有三層：輸入層、隱含層、輸出層。如圖1所示，ELM網(wǎng)絡輸入層有d個神經(jīng)元，隱含層有L個神經(jīng)元，輸出層有m個神經(jīng)元。像一些特殊的問題如典型的二分類問題，很明顯該m個神經(jīng)元是一維的[4]。只考慮隱含層輸出和輸出層，則輸出函數(shù)為：

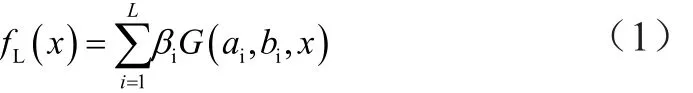
式中，ai和bi是隱含層節(jié)點的參數(shù)，βi表示第i個隱含層輸出神經(jīng)元之間的連接權值，G是隱含層輸出函數(shù)。對于相加型隱含層節(jié)點，函數(shù)G表達式為：

矩陣表達式中，L往往遠小于N，權值向量是無解的，網(wǎng)絡輸出值和實際值之間必然存在一定的誤差。因此，可以定義代價函數(shù)為：

式中參數(shù)H是隱含層的輸出矩陣，β是輸出函數(shù)與隱含層的權值[1-6]。

2.2 ELM神經(jīng)網(wǎng)絡模型建立

對于ELM神經(jīng)網(wǎng)絡模型的建立，要考慮該網(wǎng)絡的結(jié)構(gòu)，其會直接影響樣本估算的效果。根據(jù)理論經(jīng)驗，對于有兩組非線性輸入、一組非線性輸出的數(shù)據(jù)，選擇3層網(wǎng)絡就能滿足要求[4]。ELM神經(jīng)網(wǎng)絡模型如圖2所示。

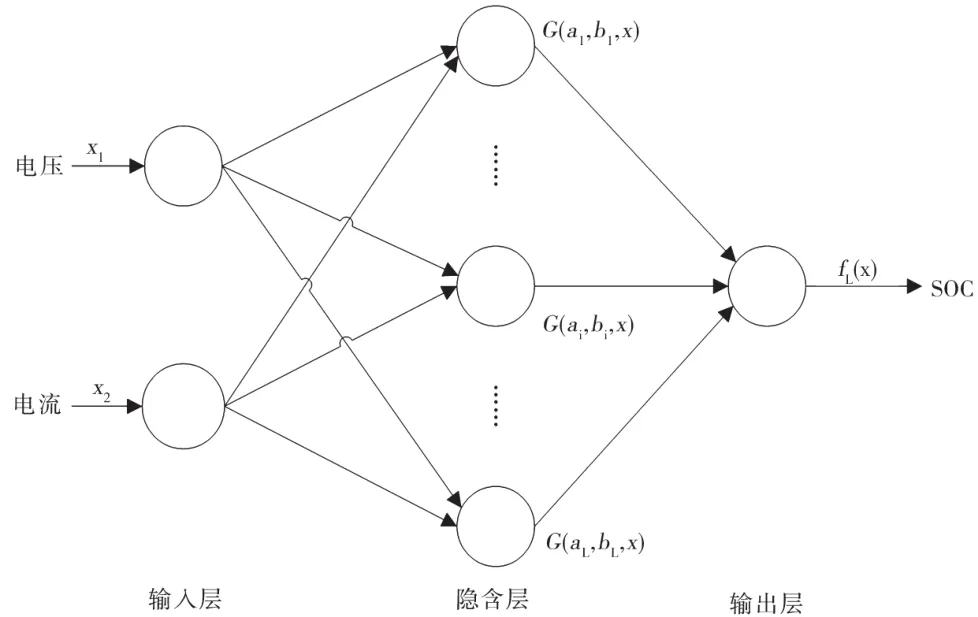
圖2 ELM神經(jīng)網(wǎng)絡模型

圖2 中設置網(wǎng)絡的輸入層有2個節(jié)點，其中設置向量為[X1，X2]，X1為AUV內(nèi)部電池的放電電壓，X2為AUV內(nèi)部電池的放電電流。因為輸出是SOC值，所以輸出層只有1個節(jié)點，設置該網(wǎng)絡輸出向量為[?L(X)]，即SOC值。經(jīng)過網(wǎng)絡訓練后，當?shù)贸鲈摼W(wǎng)絡隱含層節(jié)點數(shù)為20個左右時，可以得到比較理想的放電電壓、電流與SOC值之間的關系[2-6]。該網(wǎng)絡的輸入層、隱含層和輸出層用Sigmoid激活函數(shù)，誤差定為0.000 01[2-6]。

3 ELM神經(jīng)網(wǎng)絡模型測試電池SOC結(jié)果分析

以AUV內(nèi)部供電電池包（磷酸鐵鋰電池）為測試對象，該電池包標稱電壓為25.9 V（充滿電電壓可達29 V），標稱容量41.6 Ah。

利用MATLAB神經(jīng)網(wǎng)絡工具箱進行ELM網(wǎng)絡構(gòu)建[7-8]。將實驗測得的電池樣本數(shù)據(jù)輸入網(wǎng)絡進行訓練，并將測得的SOC實際值與SOC估計值進行比較，結(jié)果如圖3所示。從圖3可看出，采用LEM網(wǎng)絡訓練的SOC估計值曲線與SOC實際值曲線吻合度較好，差別很小。可見，該網(wǎng)絡模型訓練效果較好。

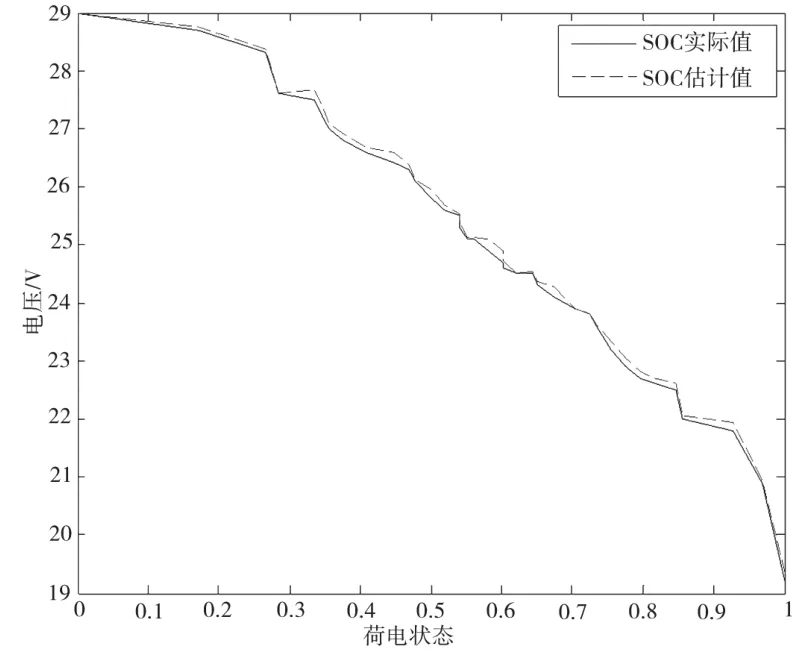
圖3 ELM神經(jīng)網(wǎng)絡估算圖

進行誤差訓練，設置網(wǎng)絡最大訓練次數(shù)為200次，期望誤差為1×10-5。經(jīng)過訓練后，它的均方誤差如圖4所示。從圖4可看出，網(wǎng)絡訓練在180次左右時達到最小均方誤差，最小均方誤差為3.82×10-5。可見，ELM神經(jīng)網(wǎng)絡泛化性能好。

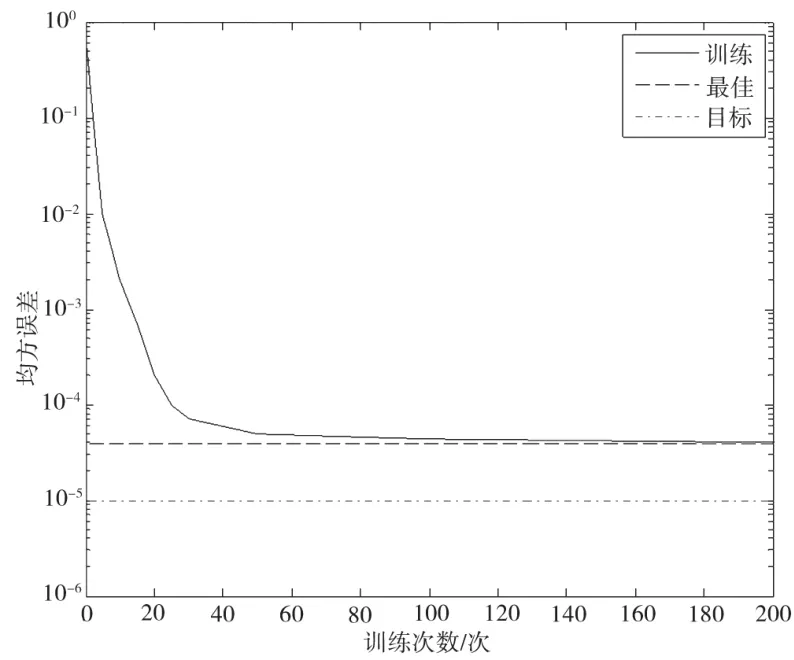
圖4 ELM神經(jīng)網(wǎng)絡訓練均方誤差圖

網(wǎng)絡樣本數(shù)據(jù)的選取對訓練效果至關重要。樣本數(shù)據(jù)的復雜性影響網(wǎng)絡的訓練效果。考慮到時間問題，分別選取恒定電流7 A、8 A放電，電壓值是每放電30 min靜置30 min測得的AUV內(nèi)部電池開路電壓，測得的數(shù)據(jù)需要歸一化處理，實驗在室溫條件下進行，結(jié)果如圖5所示。從圖5可看出，預測值與目標值吻合度較好，且放電電壓會隨著SOC值的減小逐漸降低，尤其在放電初期，電池放電電壓隨著SOC的變化較大。

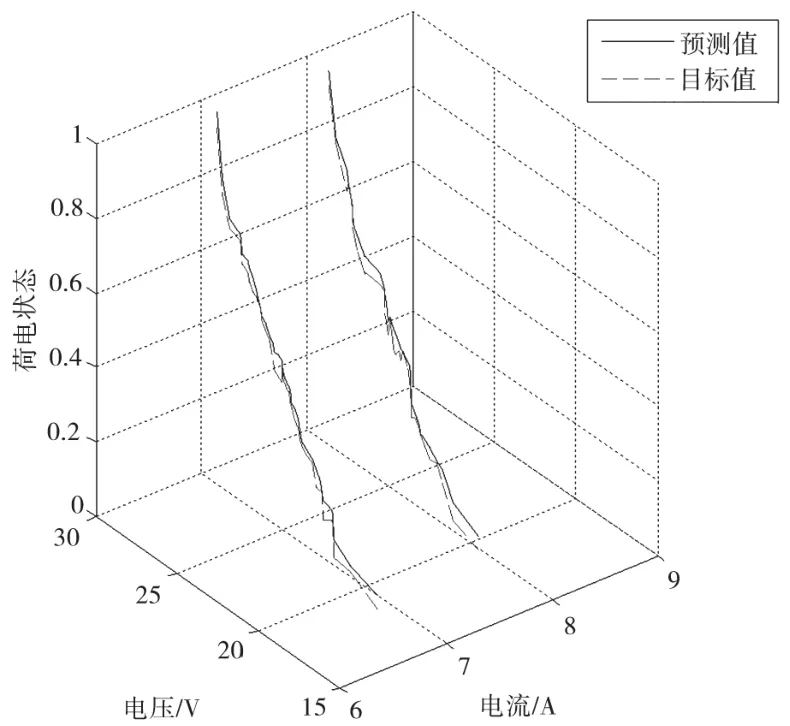
圖5 不同放電電流下的預測SOC曲線與目標SOC曲線

4 結(jié) 論

本文以AUV內(nèi)部供電電池包為測試對象，建立了基于ELM神經(jīng)網(wǎng)絡的電池SOC估算模型。利用ELM神經(jīng)網(wǎng)絡進行磷酸鐵鋰電池SOV估算具有訓練速度較快、人工干擾較少、網(wǎng)絡結(jié)構(gòu)簡單、泛化性能好的特點。實驗結(jié)果表明，ELM神經(jīng)網(wǎng)絡估算電池SOC具有可行性，準確性較高。本文只考慮了工作電壓、電流和適量的訓練樣本數(shù)據(jù)，下一步工作將諸多因素綜合考慮并且選取大量訓練樣本數(shù)據(jù)，以便得到更準確的電池SOC值。