基于NTSM的伺服電機模糊滑模控制策略研究*

黃 皓，涂群章，潘 明，蔣成明，薛金紅，李 沛

(陸軍工程大學 野戰工程學院，江蘇 南京210007)

0 引言

永磁同步電機(Permanent Magnet Synchronous Motor，PMSM)以其空間布置方便、輸出功率大、控制精度較高等優點被廣泛運用于智能機器人、新能源汽車和工業化無人機等領域。由于PMSM為非線性、多變量、強耦合性的復雜對象[1-3]，工業中一般采用常規的PID控制算法進行實時控制，常規的PID控制策略在控制過程中一般會存在啟動速度慢、調節能力弱、抗干擾性差等缺點。為了實現永磁同步電機高效率、高精密度的控制，國內外學者針對不同的電機控制系統提出了諸如神經網絡控制[4]、弱磁控制[5]、自適應控制[6-7]、滑模變結構控制(Sliding Mode Variable Structure Control，SMC)[8-10]等控制策略。其中SMC控制策略[11]由于具有對模型的參數變化不敏感、抗干擾性較好、魯棒性強等優點被國內外學者予以重視。文獻[12]提出了基于滑動模態的自適應擾動補償器的設計，解決了小慣量永磁同步電機的高精度調速控制問題。文獻[13]通過在變結構控制的基礎上設計了速度觀測反饋系統，減少了速度觀測誤差。文獻[14]通過提出一種積分型SMC控制策略，有效地提升了電機控制系統的控制精度。文獻[15]在傳統SMC控制策略的基礎上，設計了負載轉矩觀測器，較大程度減少了由于負載擾動造成的誤差。文獻[16]提出了一種自適應滑模控制策略，有效地提升了控制系統的動態性能。文獻[17]設計了一種基于滑模變結構的永磁同步電機弱磁矢量控制策略，有效地提升了永磁同步電機在高速運轉時的穩定性。

以上控制策略都有效地提高了電機控制系統的控制精度，但在控制過程中存在以下兩點不足：第一，采用的都是線性滑模面，滑模系統的跟蹤誤差無法在有限時間內收斂為0；第二，傳統SMC控制策略會產生較為嚴重的抖振現象，以上控制策略都沒有針對減弱抖振采取有效措施。針對以上兩點不足，本文設計了一種基于非線性Terminal系統的永磁同步電機Fuzzy-SMC控制算法。通過非線性Terminal滑模面代替傳統SMC控制策略中的線性滑模面，解決跟蹤誤差收斂過慢問題。以削弱抖振現象為目的制定模糊規則，通過模糊控制器實時調整滑模控制增益實現削弱抖振現象。通過MATLAB/Simulink仿真和永磁同步電機臺架測試試驗驗證了本文提出控制策略的有效性。

1 非線性Terminal滑模面設計

1.1 線性滑模面

在傳統滑模控制中，國內外學者普遍采用線性滑模面進行控制，當控制系統中的運動點趨近滑模區域時，使得跟蹤誤差逐漸削減到零[18]，跟蹤誤差的收斂速度通過調整滑模面的控制參數來改變。線性滑模面控制式如下:

s=cx1+x2

(1)

式中，c>0，x1為跟蹤誤差，x2為跟蹤誤差對時間求導。

然而傳統線性滑模面存在兩點不足之處：第一，當運動點在滑模面上趨近滑模區域時，跟蹤誤差會不斷削減，但無法在有限的時間內削減到0，這將影響永磁同步電機實現高精度的控制；第二，傳統線性滑模面采用的為等速趨近率，等速趨近率自身存在缺點，即切換帶為帶狀，當系統在切換帶運動時，最后不能趨近于原點，而是原點產生抖振帶，這種抖動可能激勵系統中存在未建模高頻成分，并可能增加控制器的負擔[19-20]。

1.2 非奇異Terminal滑模面

非奇異終端滑模面(Nonsingular Terminal Sliding Mode，NTSM)在終端滑模(Terminal Sliding Mode,TSM)[21-22]的基礎上發展而來，可以解決終端滑模面上由于控制輸入無窮大時產生的奇異現象。針對二階非線性系統：

(2)

其中x(t)=[x2(t),x2(t)]T；d(t)≤D(t)為外部擾動，D(t)為已知函數，f(x,t)為動力學方程，x2(t)為參考點位置。

參照文獻[18]，采用TSM控制策略，則設計控制器為:

(F(x,t)+D(t)+η)sgn(s))

(3)

式中:β、α為控制參數且大于0，sgn(s)為符號函數，F(x,t)為動力學方程f(x,t)的積分，λ為設計參數且λ>0,η為設計常數且η>0。

由等式(3)可得，控制策略中包含x1α/β-1x2，當x2≠0,x1=0時存在奇異區域，會使得設計控制器的值u(t)趨向+∞，此時控制器的設計沒意義。

NTSM為解決奇異性問題，滑模面設計為：

(4)

根據等式(4),此時的控制器輸出為

(5)

由式(5)可以看出，當x2≠0,x1=0，采用NTSM控制策略時，控制器輸出不會趨于+∞，可以有效解決該二階系統采用TSM控制策略時出現的奇異現象。

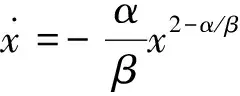
1.3 二階離散系統例證

為了驗證本文提出的NTSM控制策略的有效性，通過一個典型二階離散系統基于MATLAB/Simulink進行仿真驗證，該二階離散系統如下式：

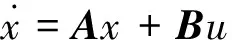
(6)

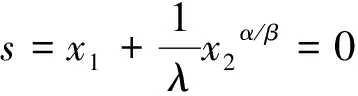
分析圖1(a)和圖2(a)可得，在兩種滑模面的控制下本文所設計的典型二階離散系統都具有較平穩的滑模運動相軌跡，控制過程中無明顯的抖動，體現了SMC控制策略在控制過程中具有較好的平穩性。分析圖1(b)和圖2(b)可得，采用線性滑模面時，控制系統到達平衡點的趨近時間約為0.61 s，而采用NTSM滑模面控制時的趨近時間約為0.16 s，趨近速度提升了70%以上，同時圖2(b)也可證明本文提出控制策略趨近過程中系統收斂性優良。分析圖1(c)和圖2(c)可得，采用線性滑模面進行控制時，控制器輸出u到達平衡點所用時間約為1.28 s，而采用NTSM滑模面對二階離散系統進行控制時所用時間約為0.78 s，由此可見本文設計的NTSM滑模面相較傳統線性滑模面達到穩態的速度更快。分析圖(d)和圖2(d)，采用線性滑模面進行控制時完成階躍響應所用時長約為1.58 s，而采用NTSM滑模面進行控制完成階躍響應所用時長為1.18 s，由此可見，通過采用本文的NTSM滑模面對二階離散系統進行實時控制時可比傳統線性滑模面提升20%以上的響應速度。

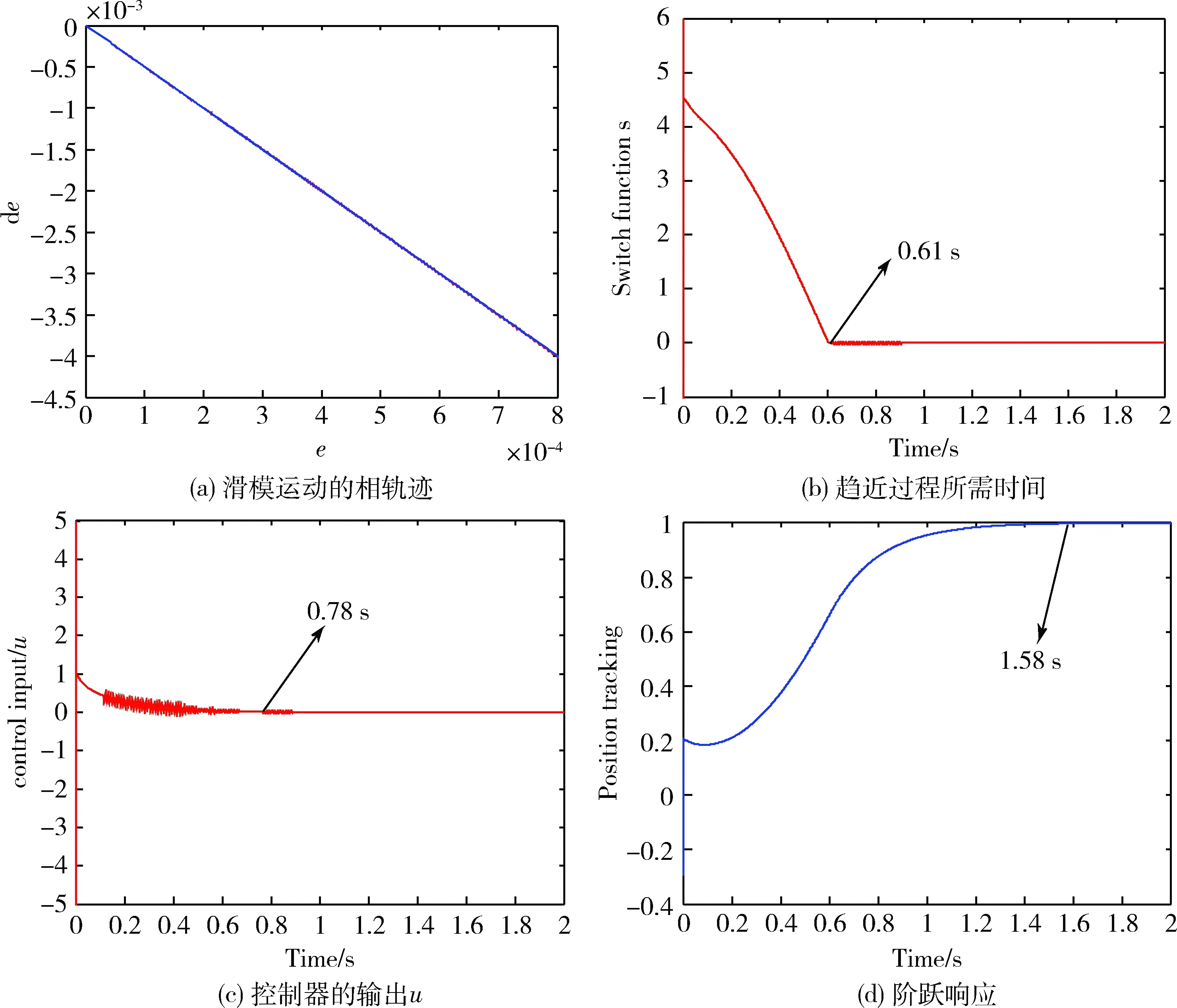
圖1 基于線性滑模面系統仿真曲線

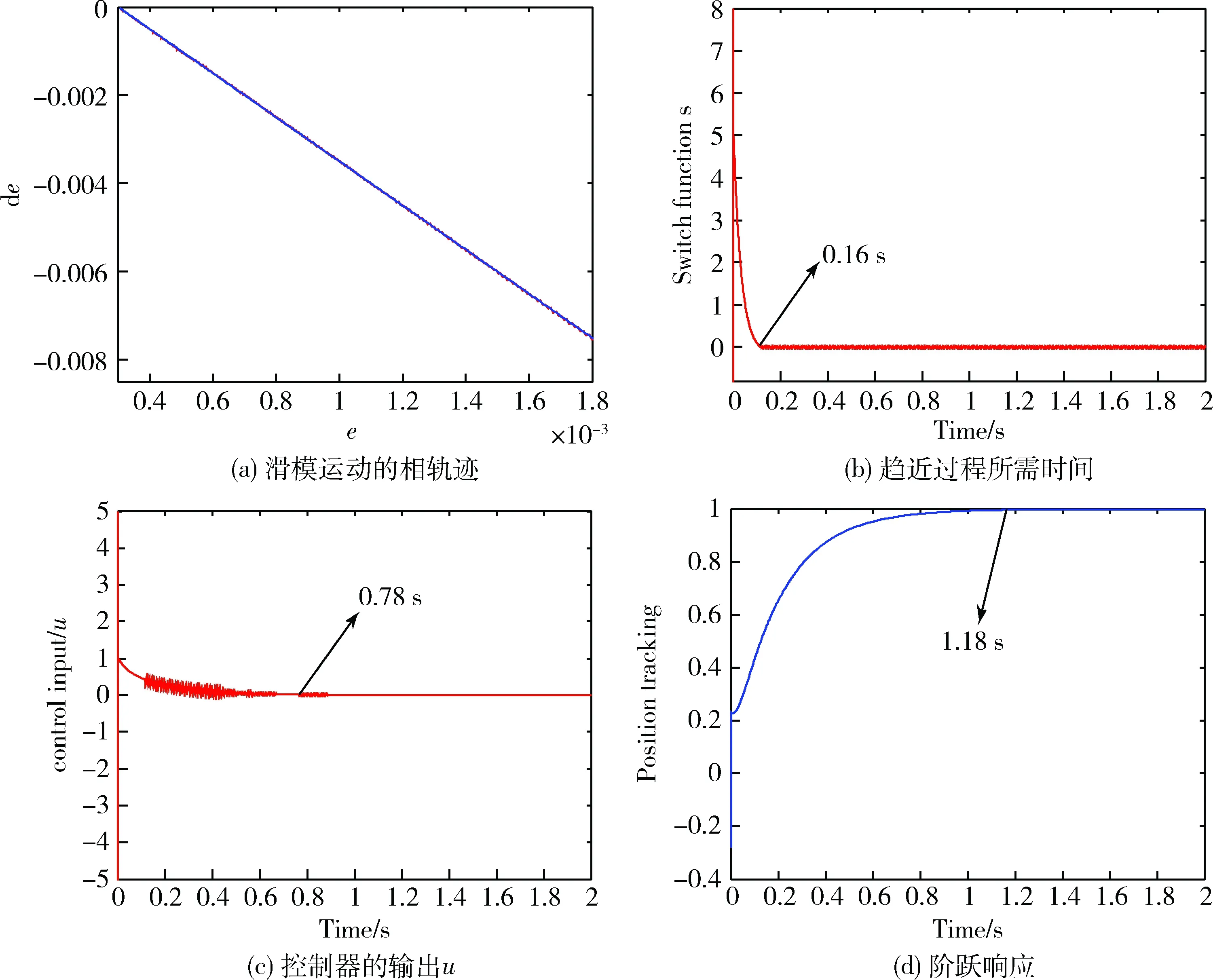
圖2 基于NTSM系統仿真曲線

綜上，本文通過一個典型二階系統分別對傳統線性滑模面和NTSM滑模面進行了基于MATLAB/Simulink的仿真，通過對比兩種不同滑模面的仿真結果，可以得出本文設計的NTSM滑模面相較傳統線性滑模面具有更快的趨近速度和響應速度。由于PMSM也為二階離散系統，可將此NTSM滑模面應用于PMSM控制系統中，提升PMSM的控制精度和響應速度。

2 PMSM非奇異SMC控制策略

2.1 PMSM數學模型的搭建

本文采用id=0的表貼式永磁同步電機轉子磁場定向控制，建立d-q坐標系下的數學模型，電壓方程為：

(7)

式中：ud、uq分別為d、q軸的電壓；id、iq分別為d、q兩軸的電流；Ld、Lq分別為d、q軸的電感；R為定子電阻；ω為電角速度。

PMSM的運動方程為：

(8)

式中：Te為PMSM的轉矩；TL為負載轉矩；J為轉動慣量。

永磁同步電機的轉矩方程為:

(9)

式中：Te為永磁同步電機的轉矩；p為電機極對數；ψ為永磁體和定子的交磁磁鏈。

針對本文設計的PMSM為目前應用最為廣泛的表貼式PMSM，該電機d軸磁感Ld與q軸磁感Lq大小相等，故有:

(10)

2.2 非奇異Terminal滑模面的設計

根據SMC控制策略，令PMSM狀態變量為:

(11)

結合式(9)和式(11)，分別對x1和x2微分可得：

(12)

采用本文所設計的NTSM滑模面，可得滑模面s為:

(13)

對s微分可得:

(14)

本文參考文獻[20]的最優參數選取，取NTSM設計參數α=3，β=5，λ=1。

為了提高速度趨近運動階段的動態品質，采用運用較為廣泛的等速趨近率，表達式為：

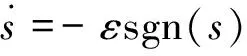
(15)

等速趨近率在實際控制過程中，趨近速度受到符號函數sgn(s)影響較大，可能會激發控制系統中未建模的高頻成分，產生較嚴重的抖振現象[21-22]。為了解決指數趨近率中的存在的問題，本文采用飽和函數sat(s,θ)代替等速趨近率中的符號函數sgn(s),則趨近率為：

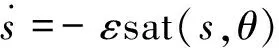
(16)

其中sat(s,θ)表達式為:

(17)

結合式(12)、式(14)、式(16)可得控制系統中的電流表達式為:

(18)

3 模糊控制器的設計

由于滑模變結構控制過程中控制系統的控制力是有限的，導致只能施予滑模上運動點有限的加速度，而滑模上的運動點受系統慣性的影響，在控制開關切換前后會出現滯后現象，從而造成抖振[23]。抖振現象在滑模運動中是必定存在的，它會在原本光滑的滑模面上疊加一個鋸齒形軌跡，如圖3所示，會較大程度上影響到系統的控制精度。針對抖振現象，以降低抖振為目標設計模糊規則，通過設計模糊控制器，實現降低抖振目的。

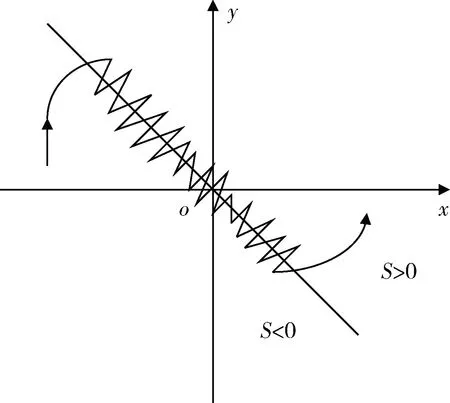
圖3 抖振現象示意圖

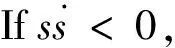
由上述模糊規則，可定義模糊控制器中的輸入模糊集和輸出模糊集：

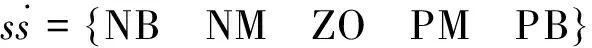
(19)

Δε={NBNMZOPMPB}

(20)

式中，NB為負大，NM為負中，ZO為零，PM為正中，PB為正大。

可得模糊控制器的隸屬函數如圖4所示。

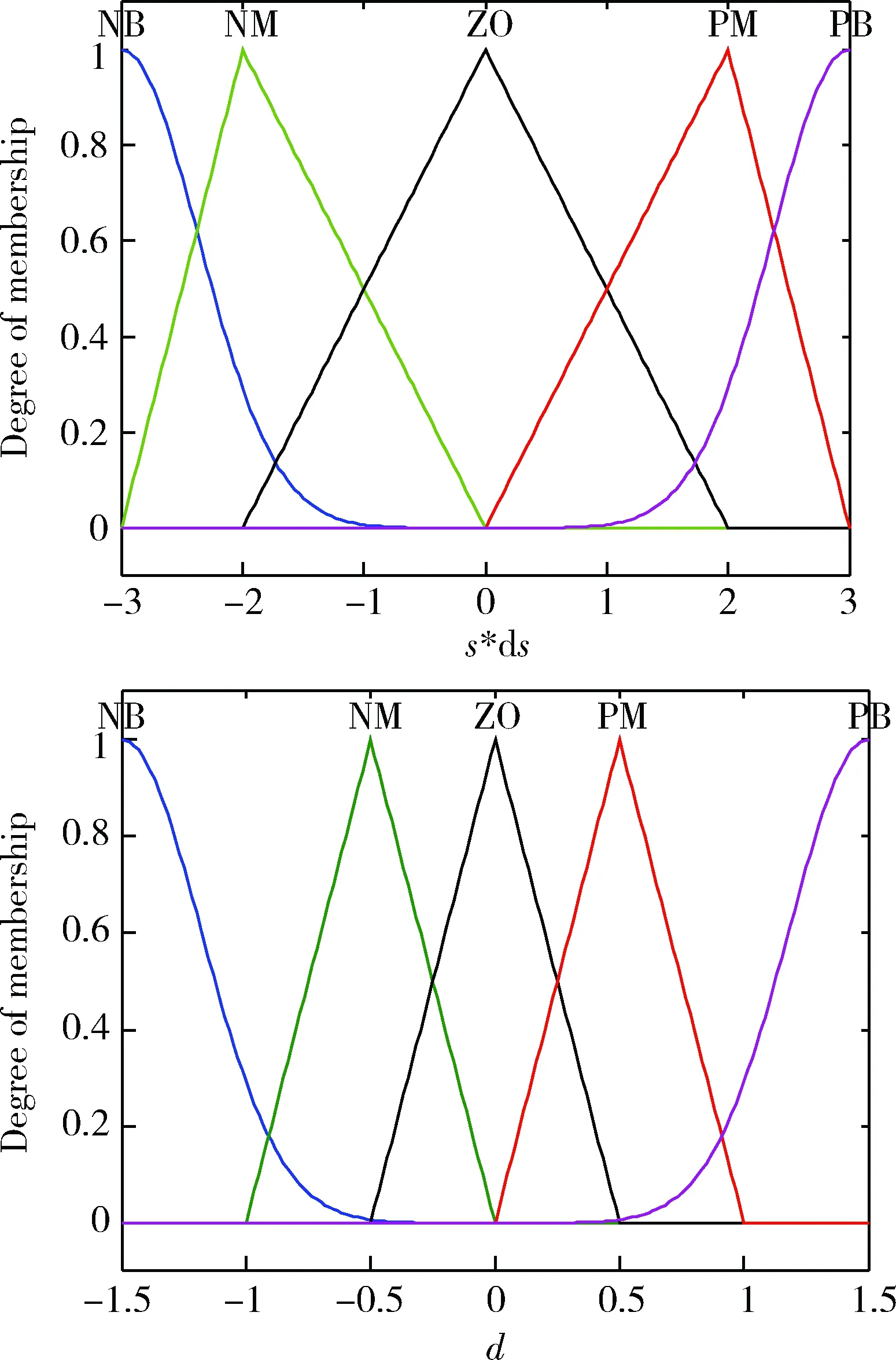
圖4 模糊控制器隸屬函數

輸入與輸出對應的模糊規則為：

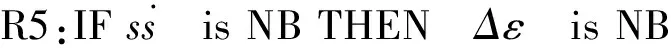
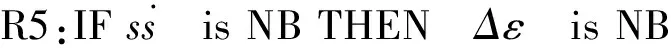
(21)

將其帶入式(21)中，可得電流方程為:

(22)

其中加入模糊控制器的NTSM控制框如圖5所示。

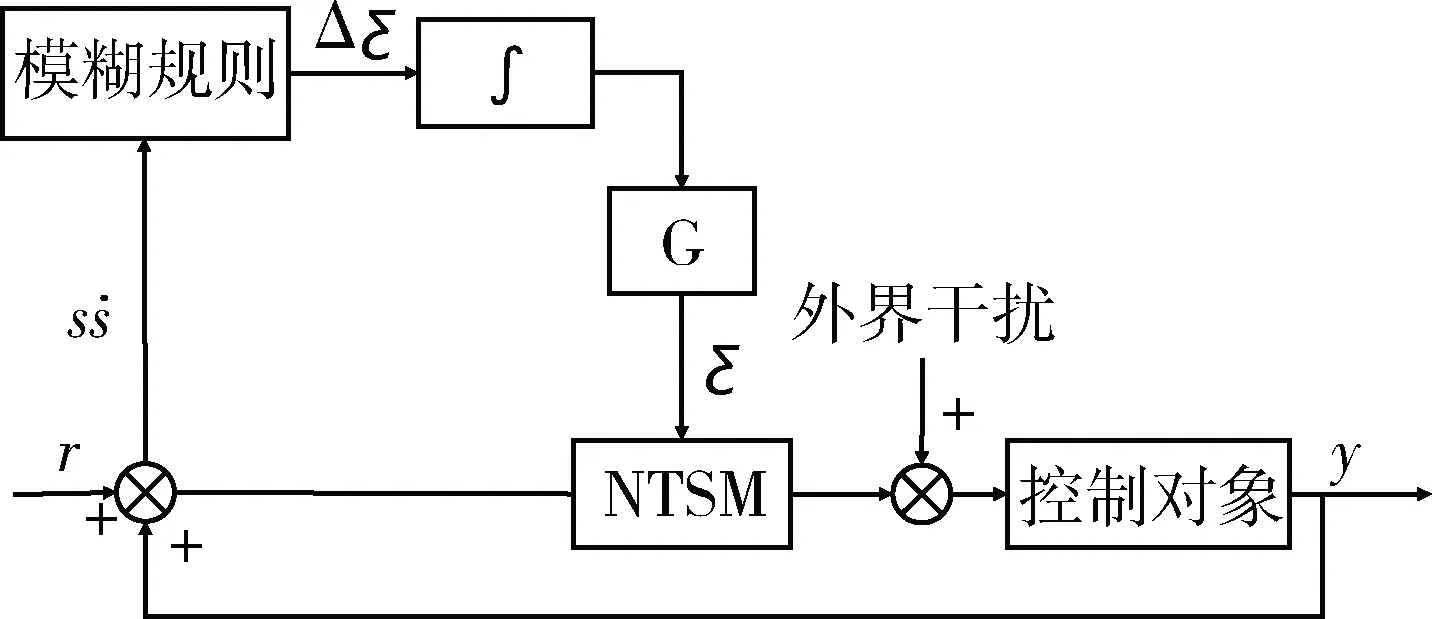
圖5 模糊滑模變結構控制框圖

4 仿真和實驗驗證

為了驗證本文提出的基于NTSM模糊滑模控制策略的有效性，基于MATLAB/Simulink搭建了電機控制系統仿真模型，并基于芯片TMS320F28335搭建了電機性能測試平臺，其中圖6為電機控制系統仿真模型控制框圖，圖7為電機性能測試臺架。

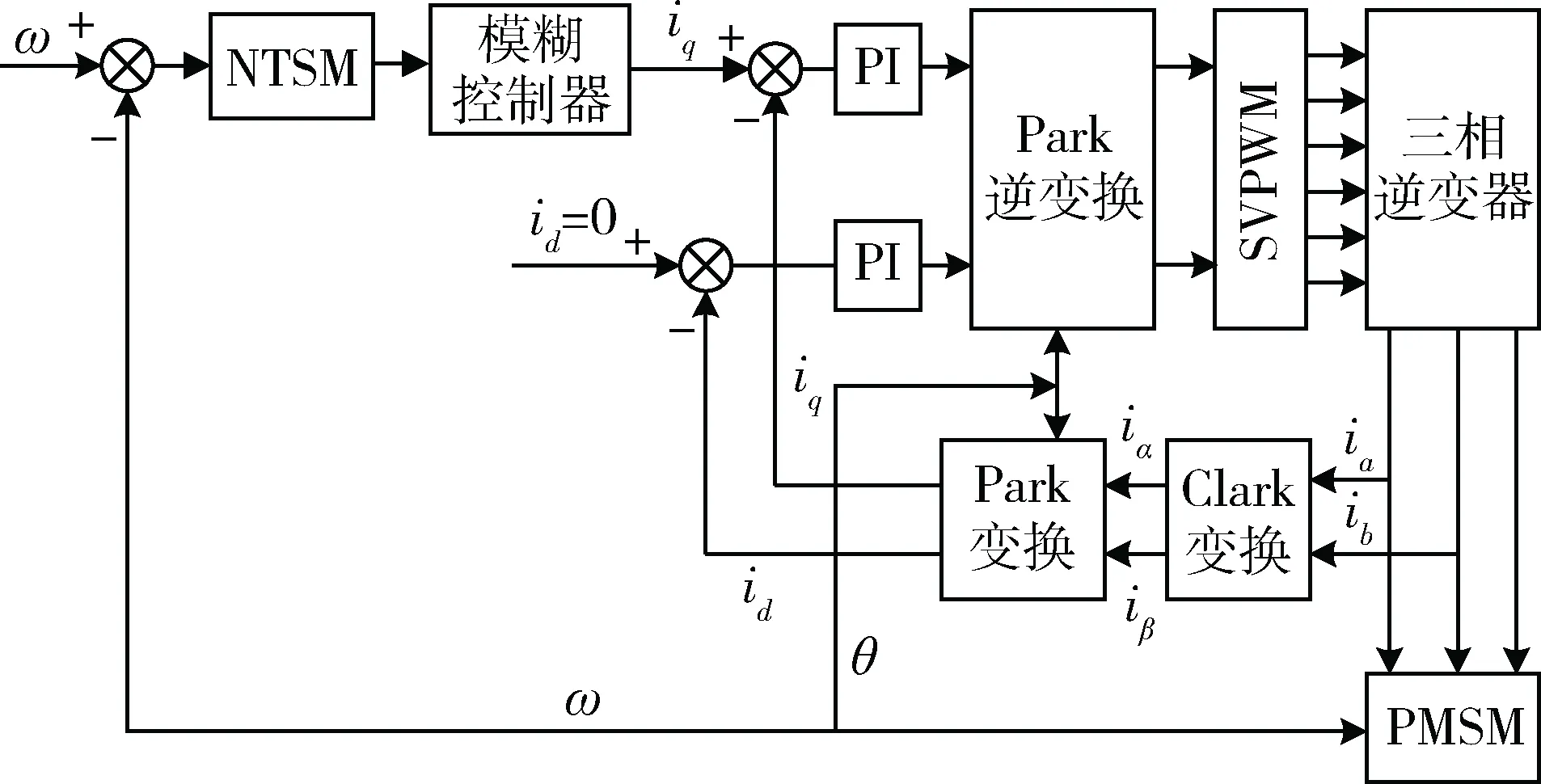
圖6 電機控制系統仿真模型控制框圖

電機控制系統在PID控制策略、普通SMC控制策略、基于NTSM模糊滑模控制策略三種控制策略下的啟動響應如圖8所示，啟動過程中仿真系統收到的轉速指令為800 r/min，圖9為仿真系統于0.3 s收到15 N·m的突增負載指令時的轉速響應，圖10為仿真系統于0.5 s時收到-15 N·m的突卸指令時的轉速響應。圖11(a)、(b)分別為PID控制策略、基于NTSM模糊滑模控制策略仿真系統負載轉矩追蹤曲線。

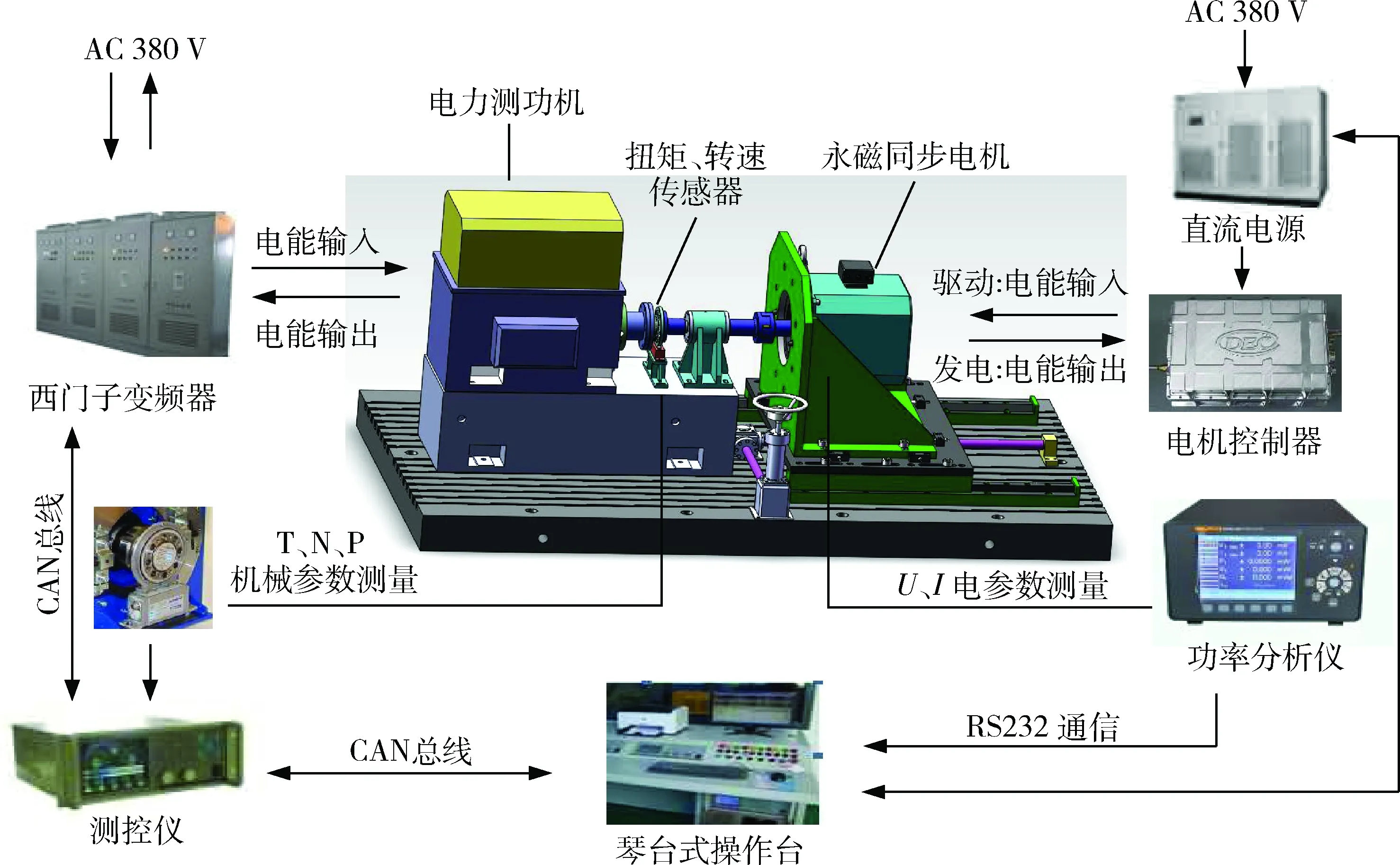
圖7 電機性能測試臺架

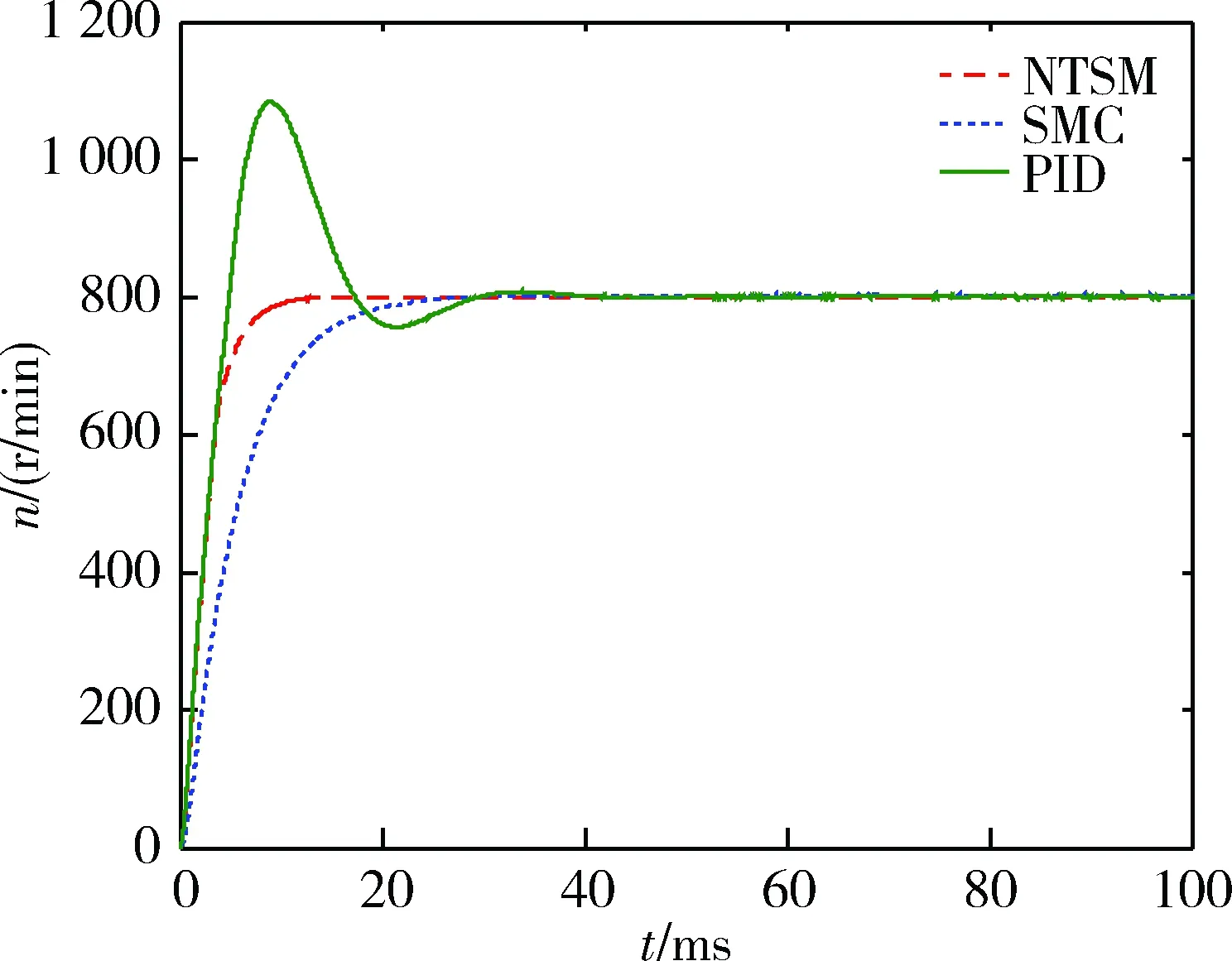
圖8 起動過程轉速仿真曲線

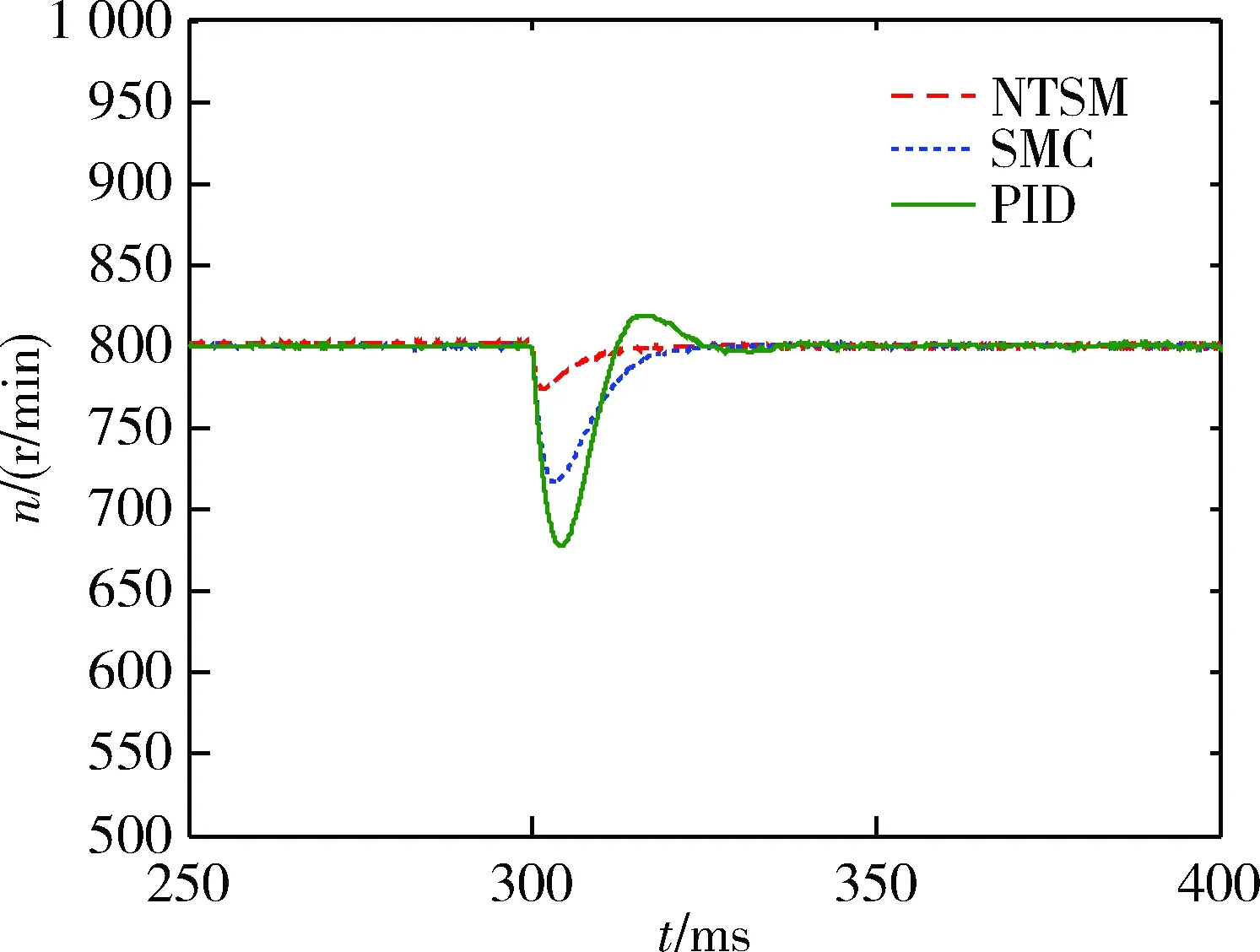
圖9 突增負載轉速仿真曲線

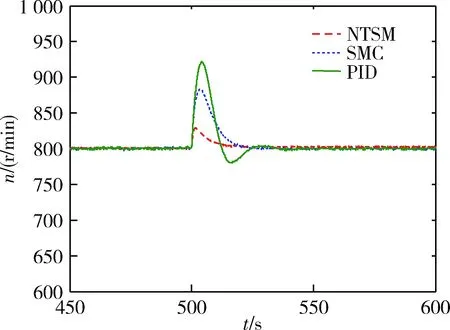
圖10 突增負載轉速仿真曲線

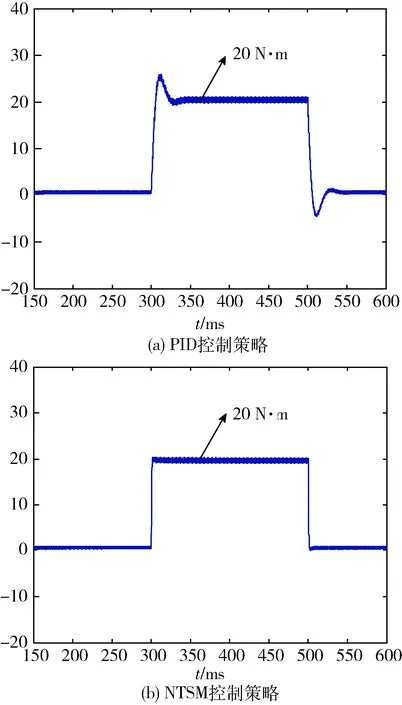
圖11 負載轉矩追蹤仿真曲線

分析和對比上述仿真結果可知，當電機控制仿真系統收到800 r/min的啟動指令時，如圖8所示，PID控制策略啟動過程中達到穩態時的響應時間約為46 ms，且存在明顯的超調現象，轉速最大波動達到300 r/min，啟動過程十分不穩定；傳統SMC控制策略啟動過程中達到穩態時的響應時間約為31 ms，且啟動過程中無超調現象，啟動性能優于PID控制策略；本文提出的基于NTSM模糊滑模控制策略啟動過程中達到穩態時的響應時間約為17 ms，與PID控制策略和傳統SMC控制策略相比，啟動響應速度分別提升了63%和45%。

當電機控制仿真系統于0.3 s收到15 N·m的突增負載指令時，如圖9所示，PID控制策略達到穩態所用時間約為40 ms，最大轉速波動約為140 r/min，且在轉速調節過程中具有超調現象；傳統SMC控制策略達到穩態時所用時間約為28 ms，最大轉速波動約為88 r/min，轉速調節過程中無超調現象；本文提出的控制策略達到穩態時所用時間約為24 ms，相較PID控制策略和傳統SMC控制策略，調節速度分別提升了40%和25%。最大轉速波動約為28 r/min，相較PID控制策略和傳統SMC控制策略，最大轉速波動分別削減了81%和56%。

電機控制仿真系統于0.5 s收到-15 N·m指令時，如圖10所示，PID控制策略突卸負載時達到穩定轉速的調節時間約為48 ms，最大轉速波動大約為135 r/min；傳統SMC控制策略達到穩定轉速的調節時間約為25 ms，最大轉速波動約為91 r/min；本文控制策略達到穩態時的調節時間為22 ms，最大轉速波動約為25 r/min。對比圖9、圖10可得，電機控制仿真系統突卸負載時轉速響應曲線與突增負載時轉速響應曲線結果相似，進一步驗證了本文提出控制策略具有較好的動態性能和抗干擾性。

電機控制系統的負載轉矩追蹤仿真曲線如圖11所示，當系統在0.3 s受到20 N·m的突增負載指令時和-20 N·m突卸負載指令時，PID控制的轉矩波動約為5 N·m，轉矩達到穩定的調節時間約為35 ms；相較PID控制策略，ISMC控制策略達到轉矩穩態的過程中幾乎無超調，且轉矩能瞬時到達給定轉矩指令值，轉矩達到穩定時較PID控制策略波動較小，具有較好的穩態性能。

電機測試臺架在起動過程時PID控制策略和本文控制策略的試驗波形如圖12所示,突增負載時的試驗波形如圖13所示，突卸負載時的試驗波形如圖14所示，三相電流波形如圖15所示。

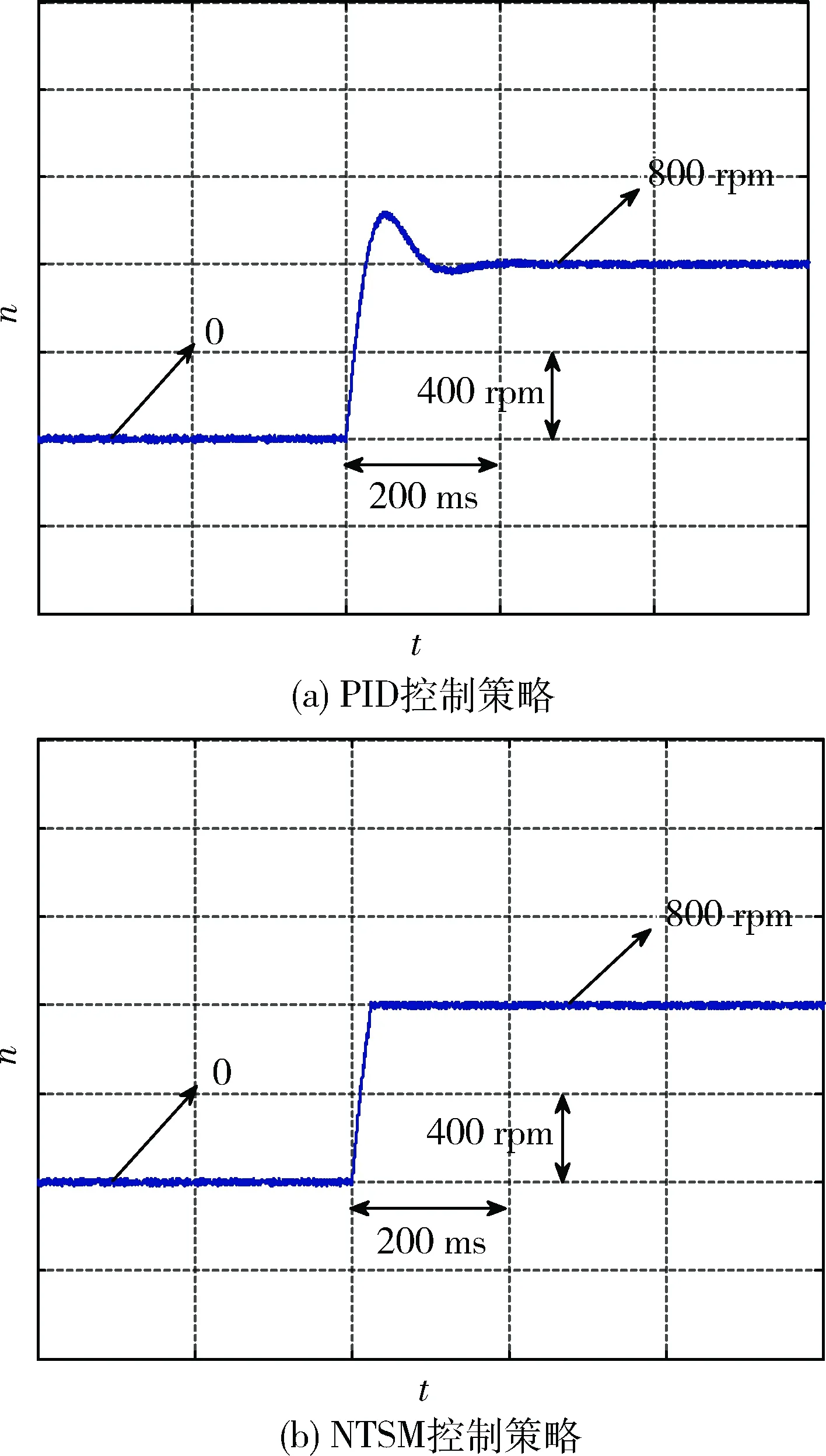
圖12 起動轉速響應試驗波形

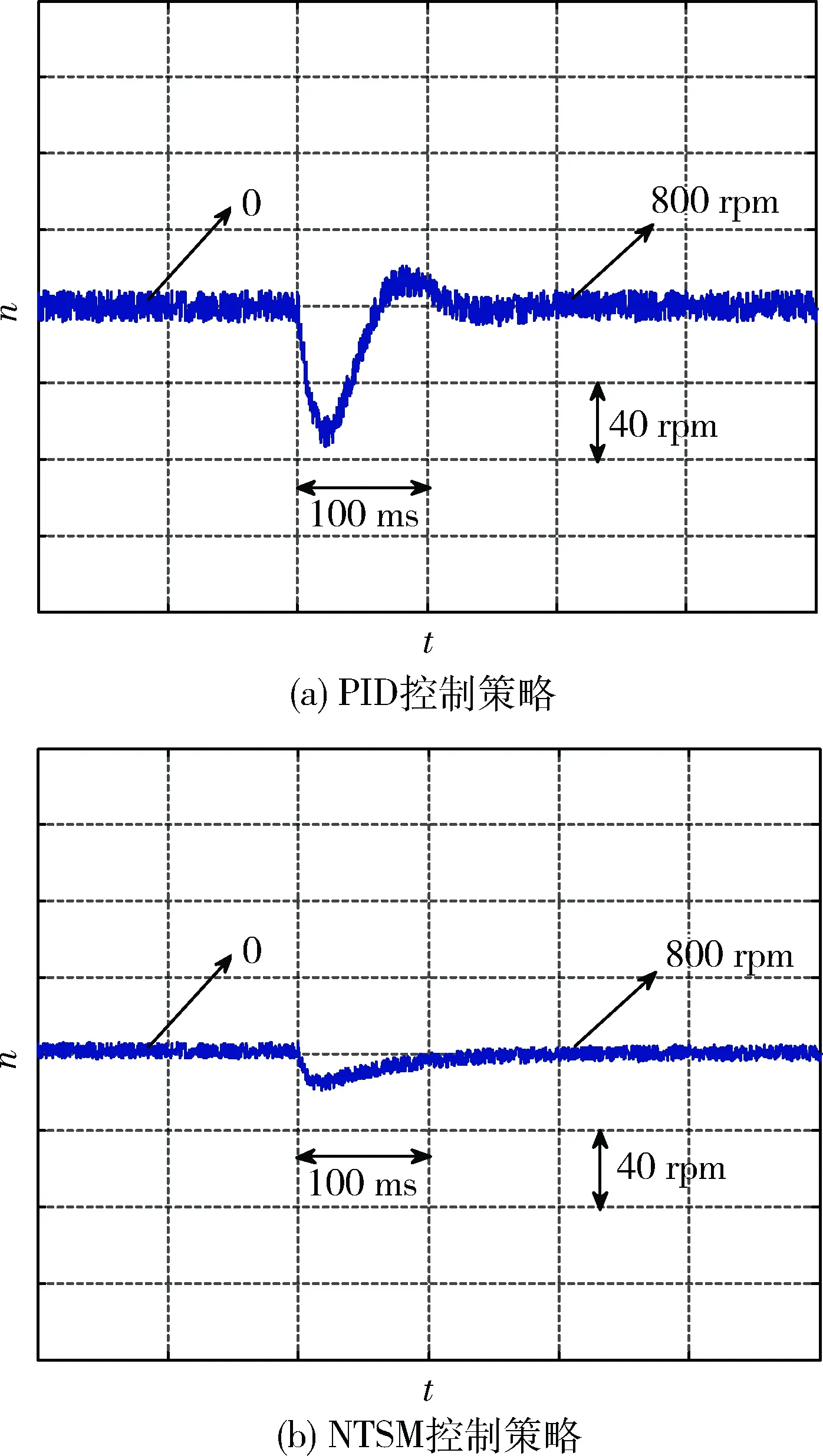
圖13 突增負載轉速響應試驗波形

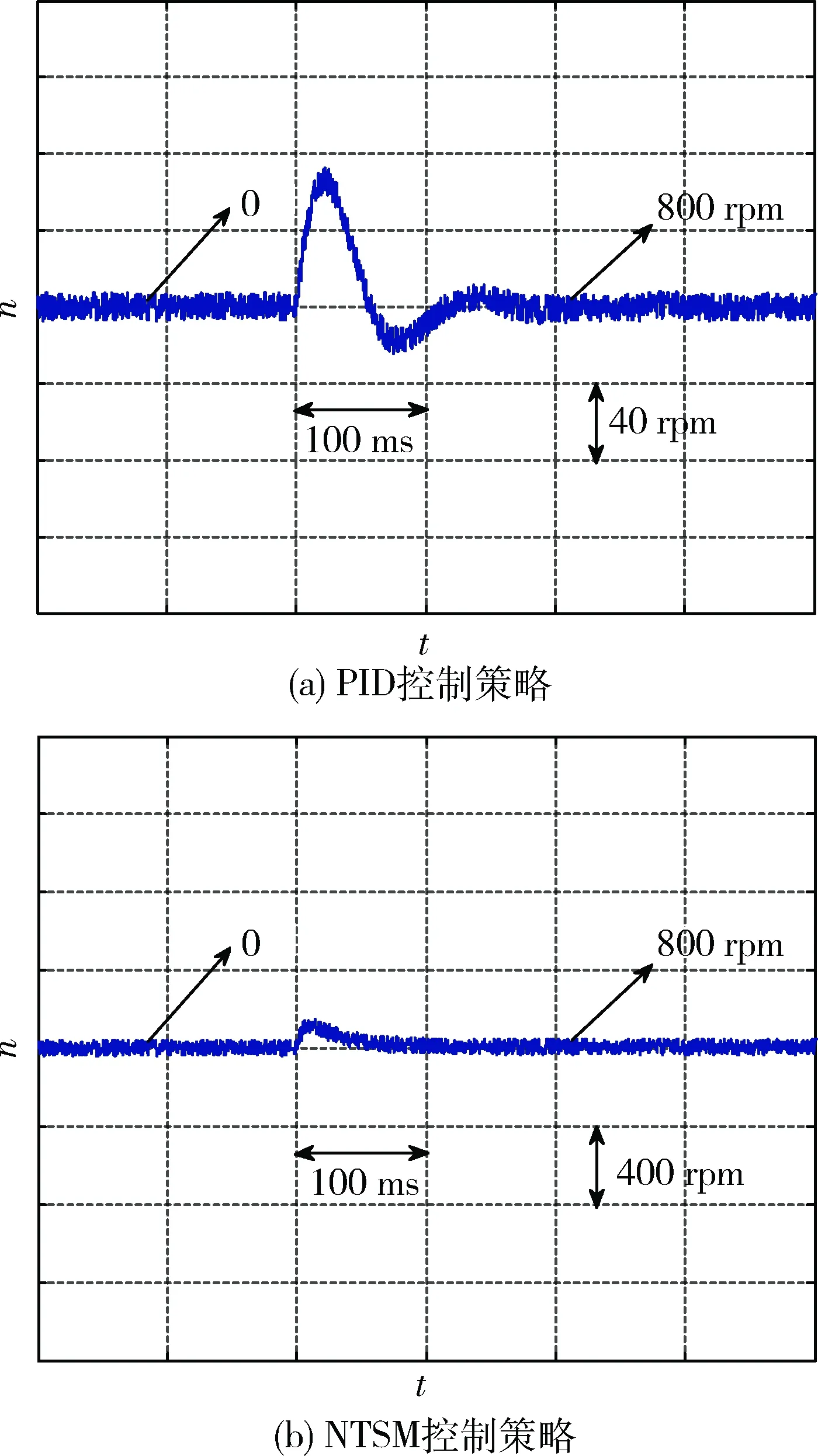
圖14 突卸負載轉速響應試驗波形

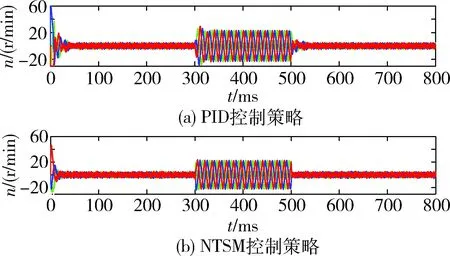
圖15 三相電流響應試驗波形

由上述仿真試驗結果可以得出：

(1)啟動過程中，如圖8和圖12所示，PID控制策略啟動速度較慢，且在調節過程中存在超調現象，普通SMC控制無超調現象，啟動速度相較PID控制策略有明顯提升。本文提出的基于NTSM滑模面的模糊滑模控制策略達到穩態時與前兩種控制策略相比，響應速度分別提升了63%和45%，具有較好的啟動響應性能。

(2)突增和突卸負載時，如圖9、圖10、圖13、圖14所示，PID控制策略達到穩態的調節速度較慢，且調節過程存在較明顯的超調現象。傳統SMC控制策略在調節過程中無超調現象，但受到SMC控制中抖振現象的影響，轉速波動較大。本文控制策略通過設計模糊控制器，使得轉速波動較小，這也是本文控制策略中有效抑制抖振現象的體現，且通過NTSM代替傳統滑模面，使得調節速度較SMC控制策略有明顯提升，展現出了較好的動態性能和魯棒性。

(3)控制過程中的三相電流響應，如圖15(a)(b)所示。本文控制策略的三相電流響應較PID控制更加平穩，達到穩態時電流波動較小，說明本文設計的基于NTSM模糊滑模控制器具有較好的抗干擾性和穩態性能。

綜上分析，本文設計的NTSM模糊滑模控制策略，通過采用NTSM代替傳統SMC控制策略中的線性滑模面，有效地提升了電機控制系統的響應速度和調節速度。通過以降低抖振為目的設定模糊規則，通過模糊控制器不斷調整控制增益使得電機控制系統受到外界負載干擾時轉速波動明顯減少，體現出了較好的動態性能和穩態性能。

5 結論

本文針對PMSM現有控制策略收斂時間長的問題，在傳統SMC控制策略的基礎上，提出采用NTSM代替線性滑模面進行控制，以加快系統收斂速度；針對SMC控制上普遍存在的抖振現象，設計模糊控制器進行有效削減。通過MATLAB/Simulink仿真和電機性能測試臺架試驗，結果表明：本文提出的NTSM模糊控制策略能有效加快系統收斂速度，提高響應性能；能有效抑制抖振現象，提高動態性能和穩態性能。本文提出的策略為實現PMSM高精度、高效率的控制提供一種有效的新方法。